Геометрические построения, необходимые при выполнении чертежей

О б ъ я с н е н и е н о в о г о м а т е р и а л а

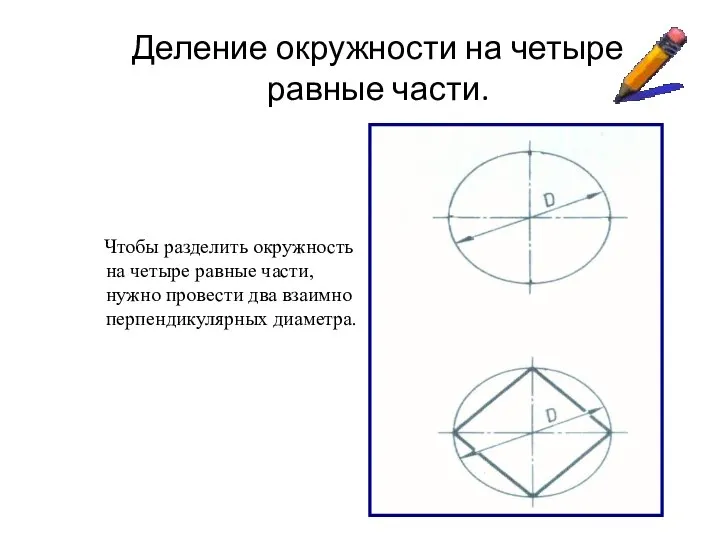
Деление окружности на четыре равные части.
Чтобы разделить окружность на четыре равные части, нужно провести два взаимно перпендикулярных диаметра.

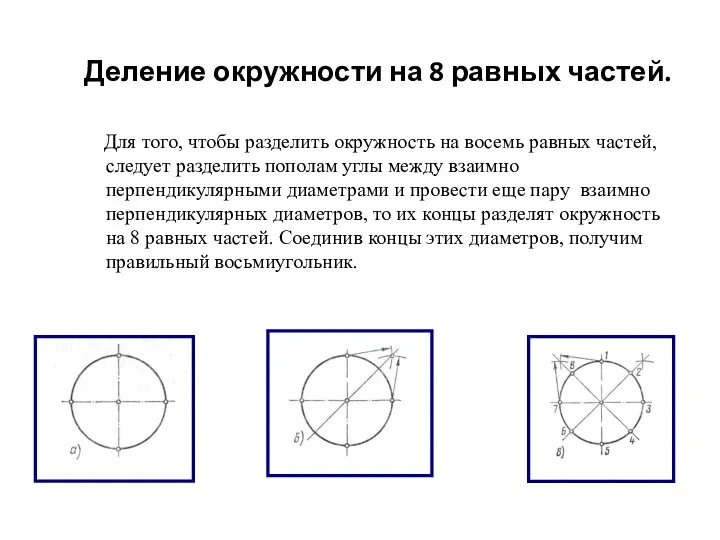
Деление окружности на 8 равных частей.
Для того, чтобы разделить окружность на восемь равных частей, следует разделить пополам углы между взаимно перпендикулярными диаметрами и провести еще пару взаимно перпендикулярных диаметров, то их концы разделят окружность на 8 равных частей. Соединив концы этих диаметров, получим правильный восьмиугольник.

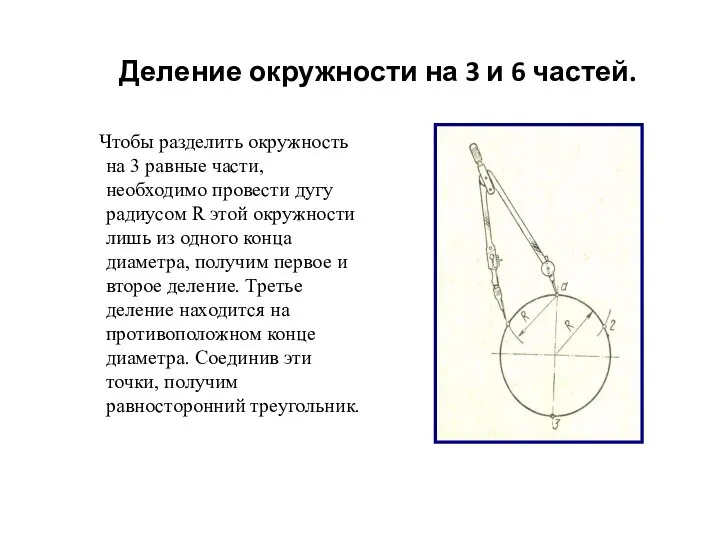
Деление окружности на 3 и 6 частей.
Чтобы разделить окружность на 3 равные части, необходимо провести дугу радиусом R этой окружности лишь из одного конца диаметра, получим первое и второе деление. Третье деление находится на противоположном конце диаметра. Соединив эти точки, получим равносторонний треугольник.

Для деления окружности на 6 частей используют равенство сторон правильного шестиугольника радиусу описанной окружности. Из противоположных концов одного из диаметров окружности описываем дуги радиусом R. Точки пересечения этих дуг с заданной окружностью разделят её на 6 равных частей. Последовательно соединив найденные точки, получают правильный шестиугольник.
Деление окружности на 6 частей.

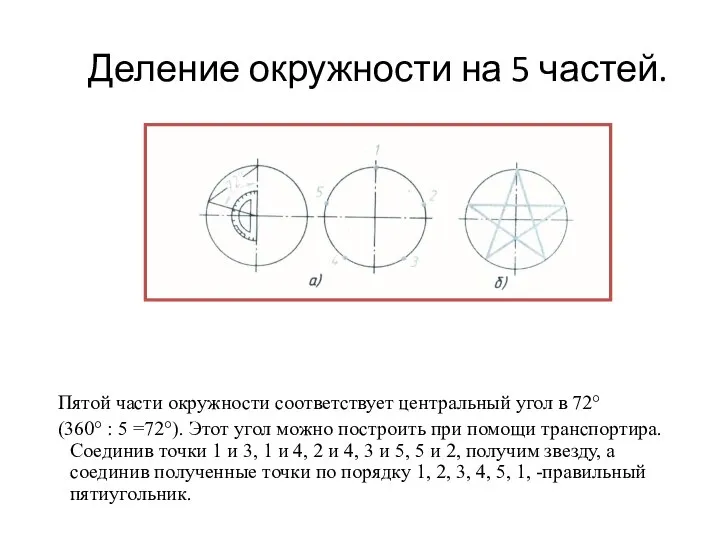
Деление окружности на 5 частей.
Пятой части окружности соответствует центральный угол в 72°
(360° : 5 =72°). Этот угол можно построить при помощи транспортира. Соединив точки 1 и 3, 1 и 4, 2 и 4, 3 и 5, 5 и 2, получим звезду, а соединив полученные точки по порядку 1, 2, 3, 4, 5, 1, -правильный пятиугольник.

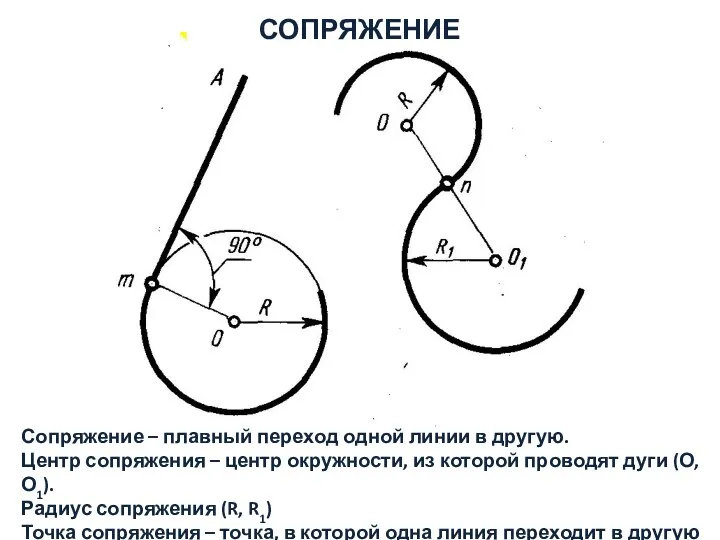
Сопряжение – плавный переход одной линии в другую.
Центр сопряжения – центр окружности, из которой проводят дуги (О, О1).
Радиус сопряжения (R, R1)
Точка сопряжения – точка, в которой одна линия переходит в другую (m, n).
СОПРЯЖЕНИЕ

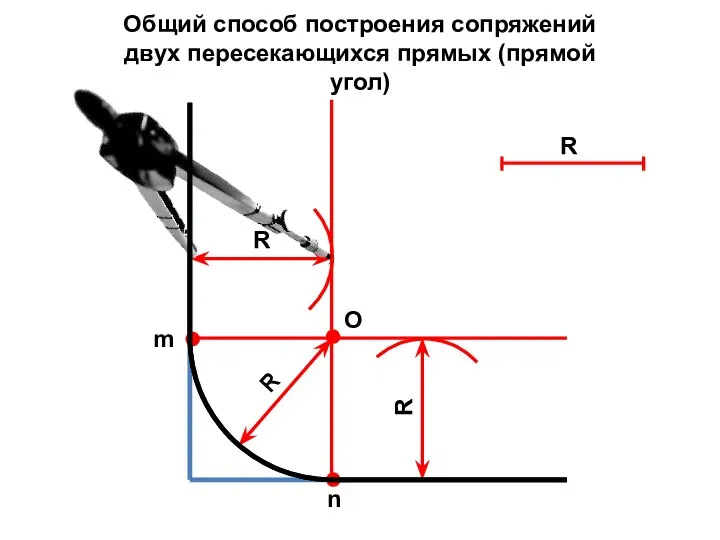
Общий способ построения сопряжений двух пересекающихся прямых (прямой угол)
R
R
О
R

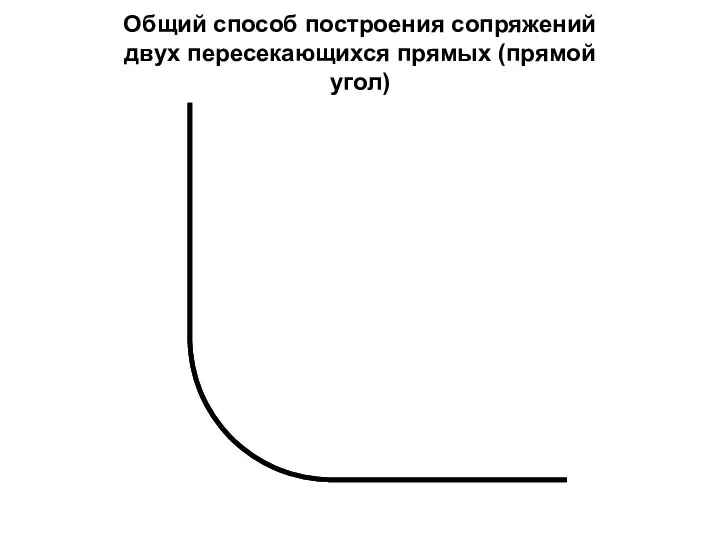
Общий способ построения сопряжений двух пересекающихся прямых (прямой угол)

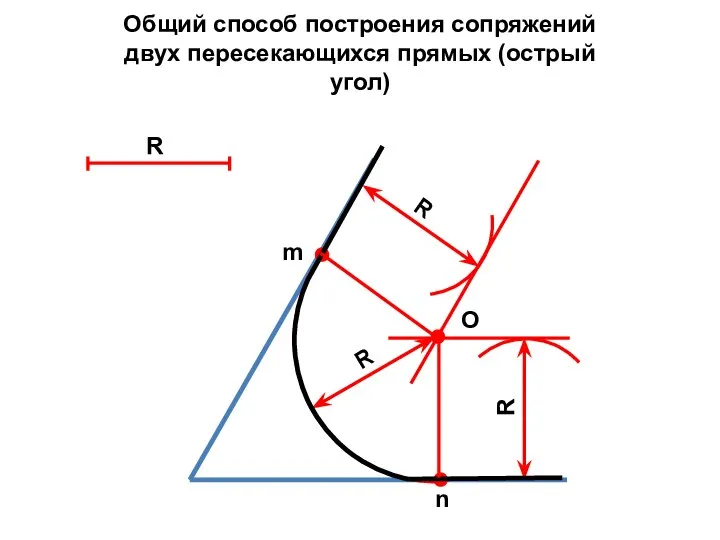
Общий способ построения сопряжений двух пересекающихся прямых (острый угол)
R
R
О
R

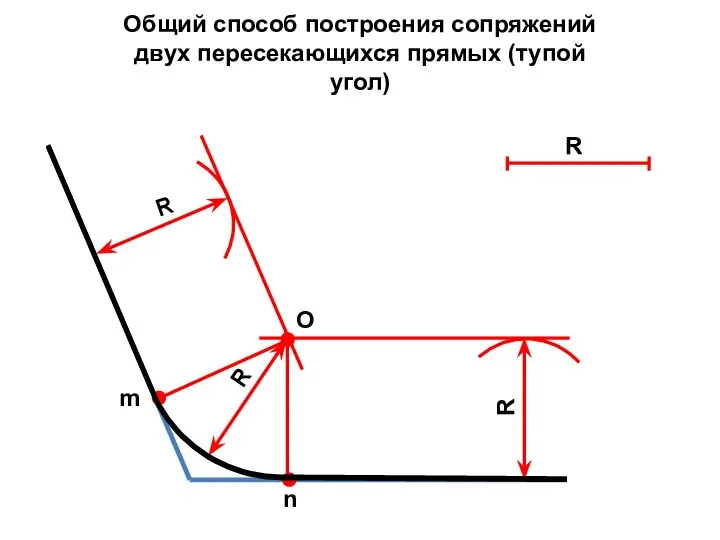
Общий способ построения сопряжений двух пересекающихся прямых (тупой угол)
R
R
О
R

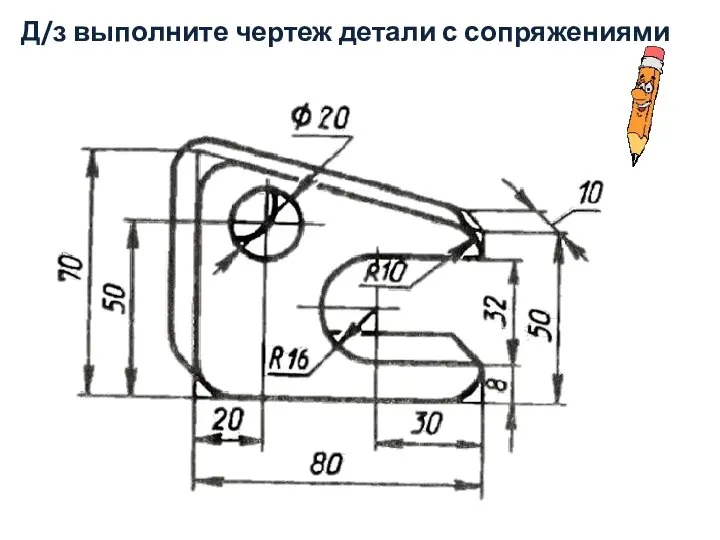
Д/з выполните чертеж детали с сопряжениями

Итоги урока.
Что нового вы узнали на уроке?
Для чего нужно знать правила деления окружности на равные части?