Геометрический сундучок

?
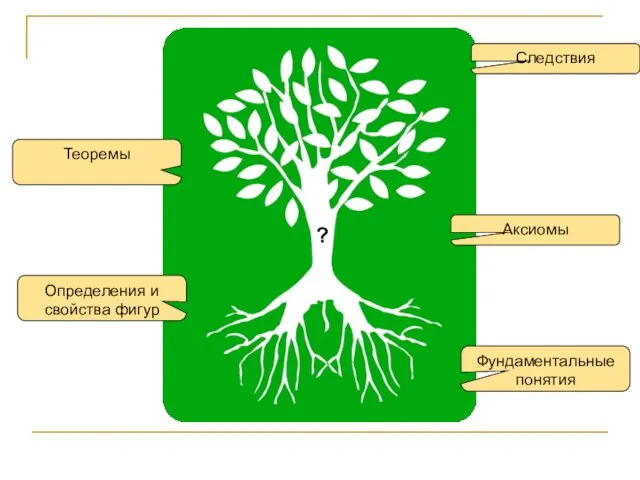
Фундаментальные понятия
Определения
Свойства геометрических фигур
Теоремы

Фундаментальные (неопределяемые)понятия
Точка
Прямая
Плоскость
Назад в сундучок

Определения
Отрезок
Луч
Угол
Равные фигуры
Середина отрезка
Биссектриса угла
Единица измерения
Длина отрезка
Градус, секунда, минута
Градусная мера угла
Смежные углы
Вертикальные углы
Треугольник
…
Назад в сундучок

Свойства геометрических фигур
Биссектриса делит угол пополам.
Сумма смежных углов равна 1800.
Вертикальные углы равны.
Две прямые, перпендикулярные к третьей, не пересекаются.
…
Назад в сундучок

Теоремы
Первый признак равенства треугольников (по двум сторонам и углу между ними).
Существование и единственность перпендикуляра к прямой.
…
Назад в сундучок

?
Фундаментальные понятия
Аксиомы
Теоремы
Следствия
?
Определения и свойства фигур

Аксиомы
Каждой прямой принадлежит по крайней мере две точки.
Имеются по крайней мере три точки, не лежащие на одной прямой.
Через любые две точки проходит прямая, и притом только одна.
Из трех точек прямой одна и только одна лежит между двумя другими.
Каждая точка О прямой разделяет её на две части (два луча) так, что две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.

Каждая прямая а разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а.
Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.
На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
От любого луча в данную полуплоскость можно отложить угол, равный данному неразвернутому углу, и притом только один.
Любой угол hk можно совместить наложением с равным ему углом h1k1 двумя способами: 1) так, что луч h совместиться с лучом h1, а луч k – с лучом k1; 2) так, что луч h совместится с лучом k1, а луч k – с лучом h1.

Любая фигура равна самой себе.
Если фигура Ф равна фигуре Ф1, то фигура Ф1 равна фигуре Ф.
Если фигура Ф1 равна фигуре Ф2, а фигура Ф2 равна фигуре Ф3, то фигура Ф1 равна фигуре Ф3.
При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.
При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Историческая справка
Аксиоматический подход к построению геометрии зародился в глубокой древности и был изложен в знаменитом сочинении «Начала» древнегреческого ученого Евклида (примерно 365-300 гг. до н.э.)
Некоторые из аксиом Евклида и сейчас используются в курсах геометрии, а сама геометрия, изложенная в началах, называется евклидовой геометрией.

?
Фундаментальные понятия
Следствия
Аксиомы
Теоремы