Содержание
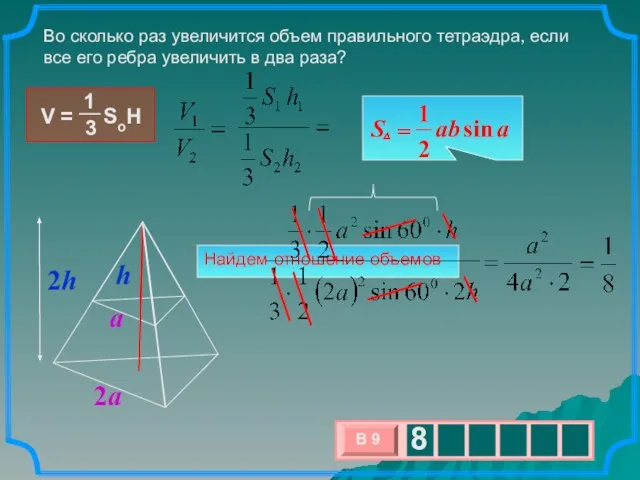
- 2. Найдем отношение объемов Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в
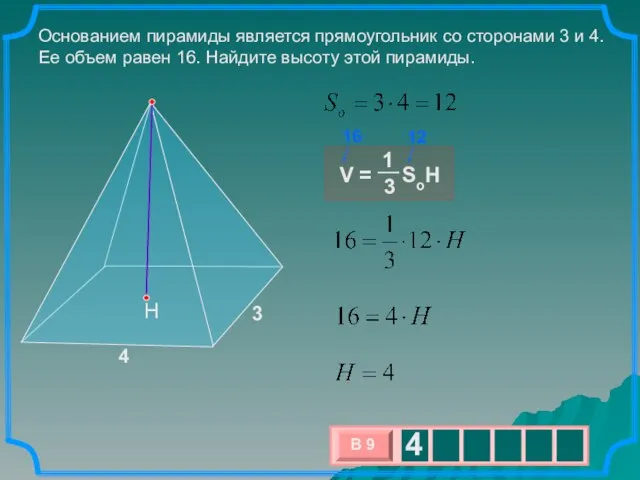
- 3. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой
- 4. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна . 1 1
- 5. . Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен . 2
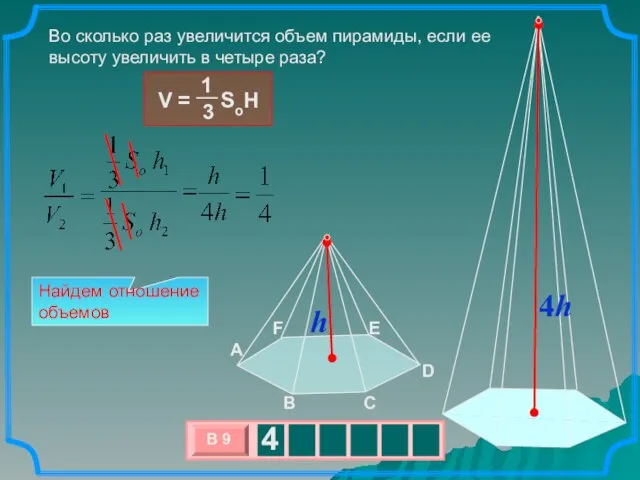
- 6. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза? Найдем отношение объемов
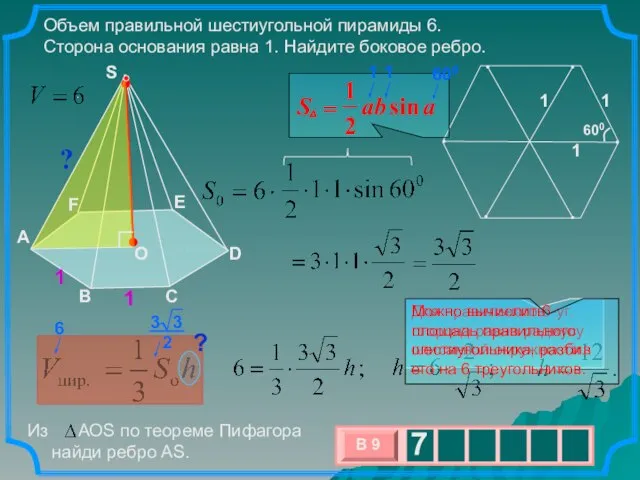
- 7. . Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро. A F B
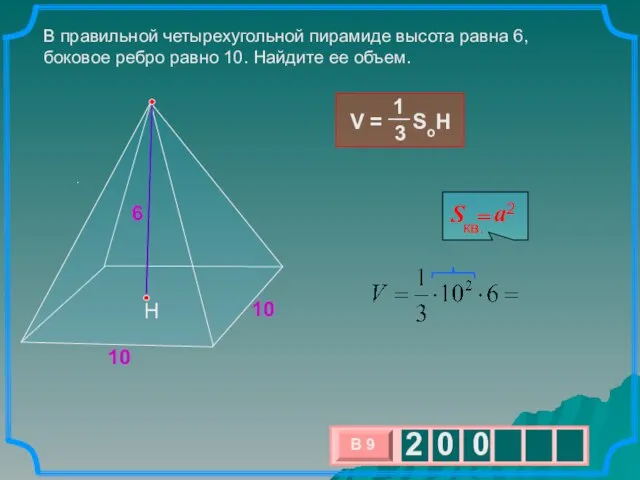
- 8. . В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем. 6
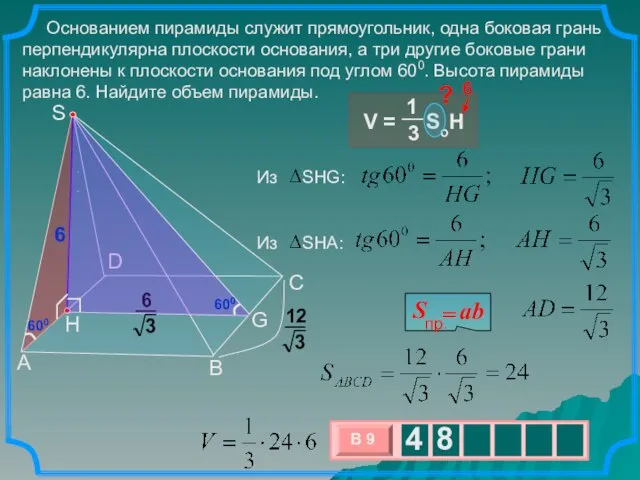
- 9. . Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани
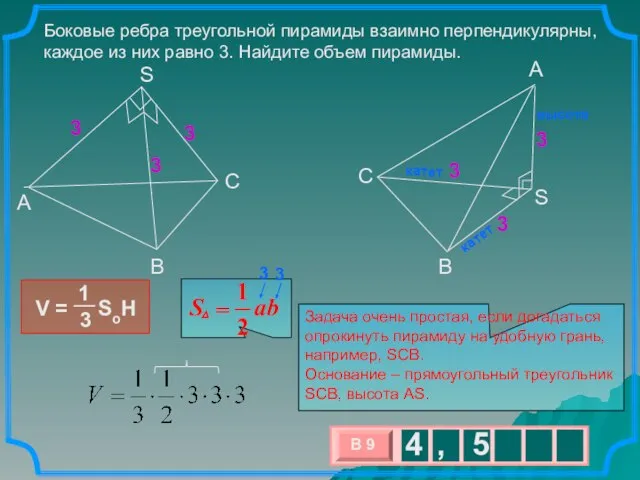
- 10. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды. Задача очень
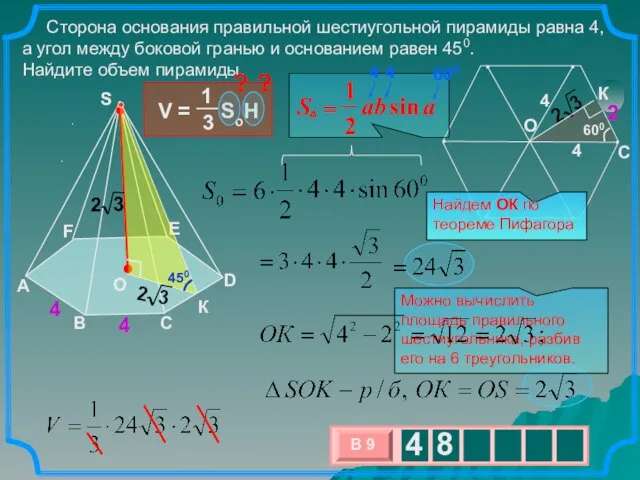
- 11. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 450.
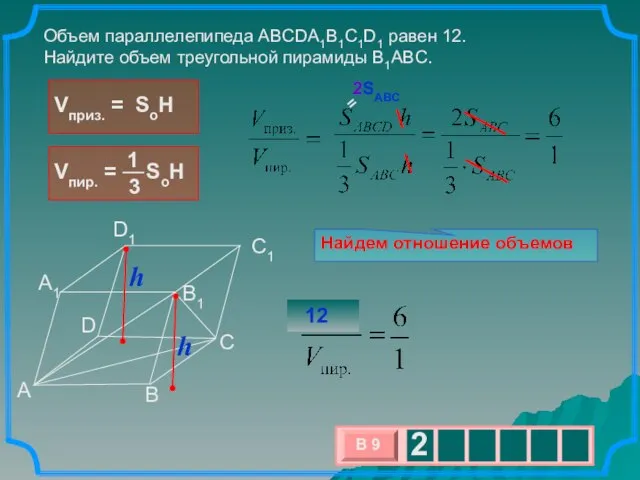
- 12. Найдем отношение объемов Объем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC. B C D
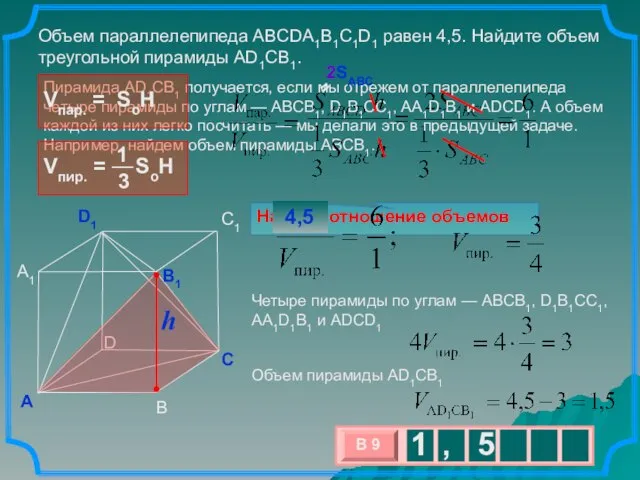
- 13. Пирамида AD1CB1 получается, если мы отрежем от параллелепипеда четыре пирамиды по углам — ABCB1, D1B1CC1, AA1D1B1
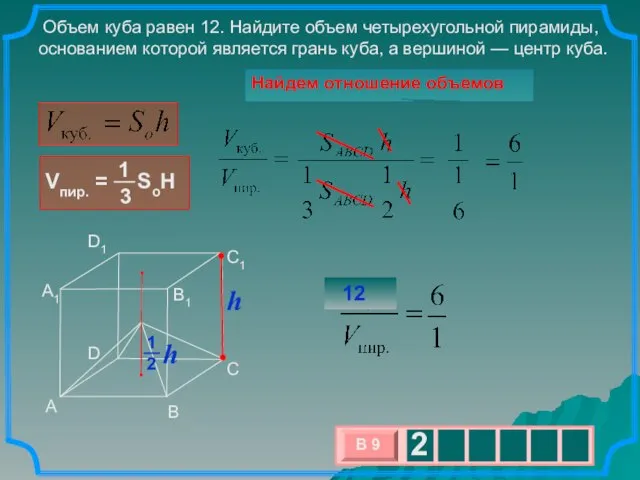
- 14. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной —
- 15. От треугольной призмы, объем которой равен 150, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания
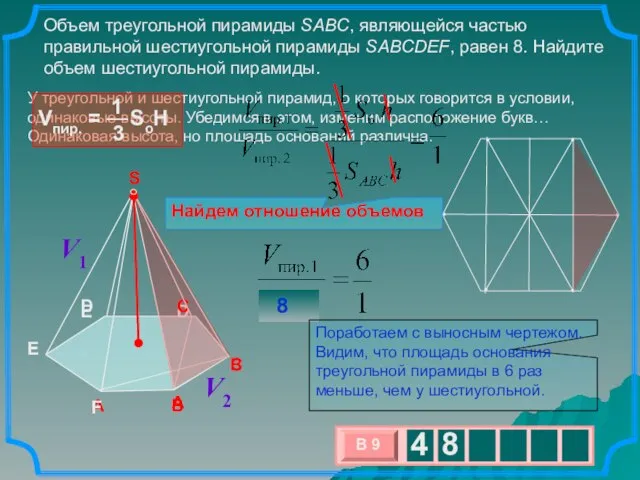
- 16. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 8. Найдите объем шестиугольной пирамиды.
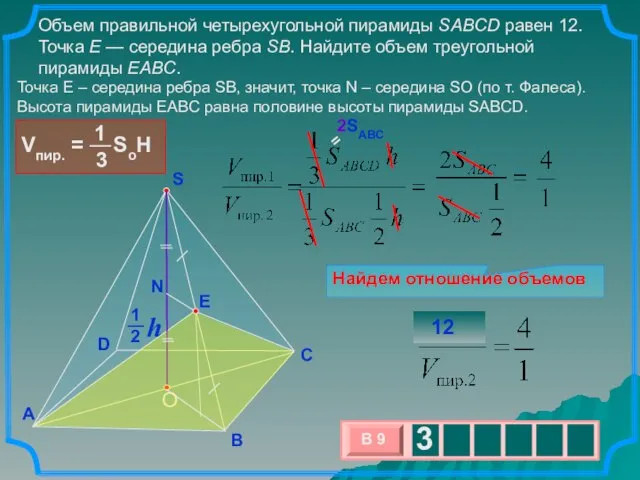
- 17. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной
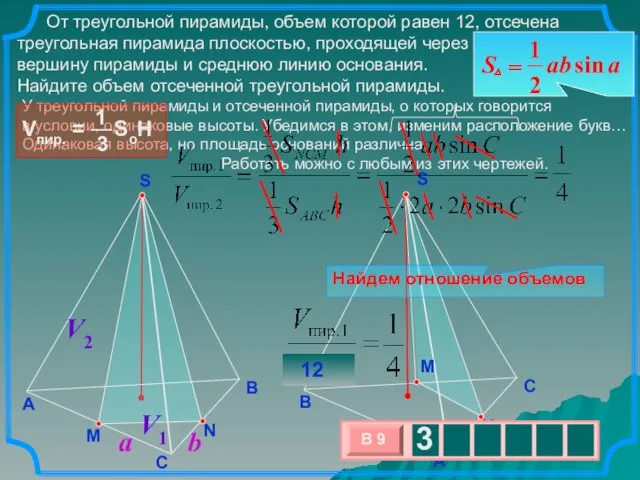
- 19. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и
- 21. Скачать презентацию




 «Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами»
«Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами» Роспись петуха по мотивам Филимоновской росписи
Роспись петуха по мотивам Филимоновской росписи Гражданское право. Понятие и виды сроков в гражданском праве
Гражданское право. Понятие и виды сроков в гражданском праве Модернизм
Модернизм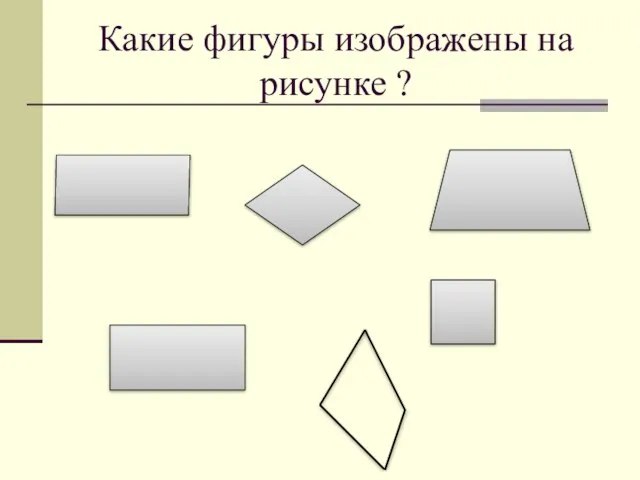 Какие фигуры изображены на рисунке ?
Какие фигуры изображены на рисунке ? Перенос слова переносятся по слогам
Перенос слова переносятся по слогам Принтеры
Принтеры Методическая разработка «Создание презентаций» Элективный курс для 10 класса.
Методическая разработка «Создание презентаций» Элективный курс для 10 класса. Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне
Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне Федеральное Собрание РФ
Федеральное Собрание РФ Инжиниринг нефтехимии и нефтегазопереработки
Инжиниринг нефтехимии и нефтегазопереработки Китайский клуб МИИТа
Китайский клуб МИИТа Мой город, с тебя начинается Родина (город Сатка)
Мой город, с тебя начинается Родина (город Сатка) Спартакиада пенсионеров муниципального образования Город Гатчина
Спартакиада пенсионеров муниципального образования Город Гатчина Эры. Основные события органического мира
Эры. Основные события органического мира Презентация на тему Операционные системы на мобильных устройствах
Презентация на тему Операционные системы на мобильных устройствах  Живопись
Живопись Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы
Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70
Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70 МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942)
МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942) Векторы в пространстве и не только
Векторы в пространстве и не только Презентация на тему История развития отечественной вычислительной техники
Презентация на тему История развития отечественной вычислительной техники Трансформация изображения через трансформацию формы - серия открыток
Трансформация изображения через трансформацию формы - серия открыток ОРНАМЕНТЫ в национальном костюме
ОРНАМЕНТЫ в национальном костюме Цветник для солнечного места “Степной бриз ”
Цветник для солнечного места “Степной бриз ” Презентация на тему Тургенев. Стихи в прозе
Презентация на тему Тургенев. Стихи в прозе 287 Воскресшему служу я
287 Воскресшему служу я Берлину заменить Северный поток-2 другим проектом
Берлину заменить Северный поток-2 другим проектом