Геометрия 11 класс

Если в одной из 2 параллельных плоскостей взять окружность, и из каждой ее точки восстановить перпендикуляр до пересечения со второй плоскостью, то получится тело, ограниченное двумя кругами и поверхностью, образованной из перпендикуляров, это тело называется цилиндром.
1.Как можно получить цилиндр
Круги, лежащие в параллельных плоскостях, называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей оснований –называются образующими цилиндра.

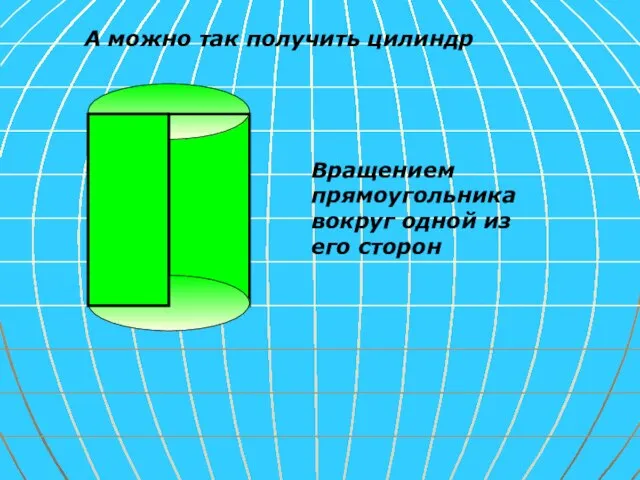
А можно так получить цилиндр
Вращением прямоугольника вокруг одной из его сторон

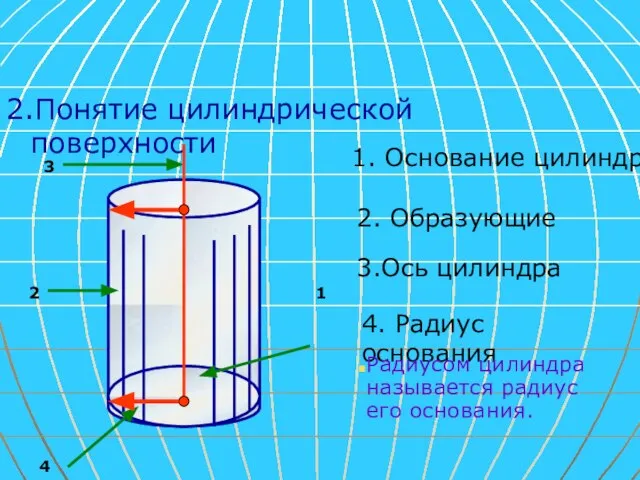
2.Понятие цилиндрической поверхности
1
2
3
4
1. Основание цилиндра
2. Образующие
3.Ось цилиндра
4. Радиус основания
4
Радиусом цилиндра называется радиус его основания.

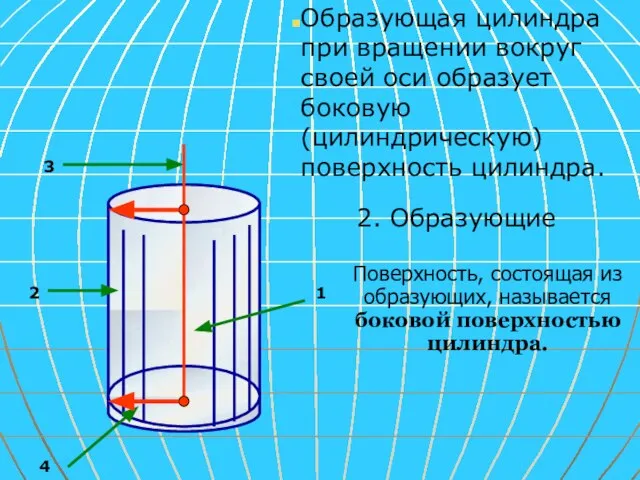
Образующая цилиндра при вращении вокруг своей оси образует боковую (цилиндрическую) поверхность цилиндра.
1
2
3
4
4
2. Образующие
Поверхность, состоящая из образующих, называется боковой поверхностью цилиндра.

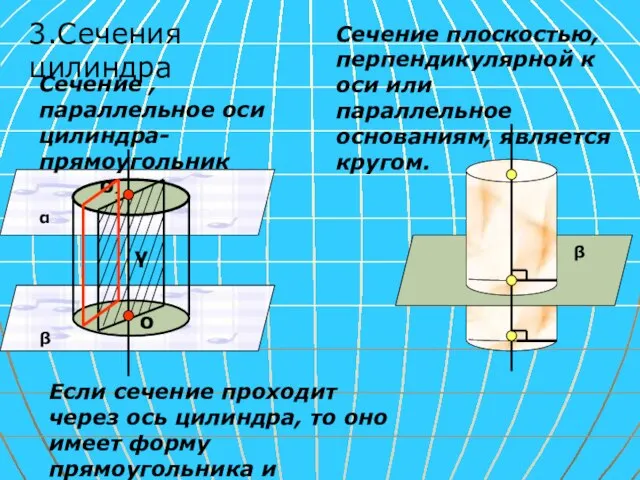
Если сечение проходит через ось цилиндра, то оно имеет форму прямоугольника и называется «осевым»
Сечение плоскостью, перпендикулярной к оси или параллельное основаниям, является кругом.
β
α
β
о
о1
γ
3.Сечения цилиндра
Сечение , параллельное оси цилиндра-прямоугольник

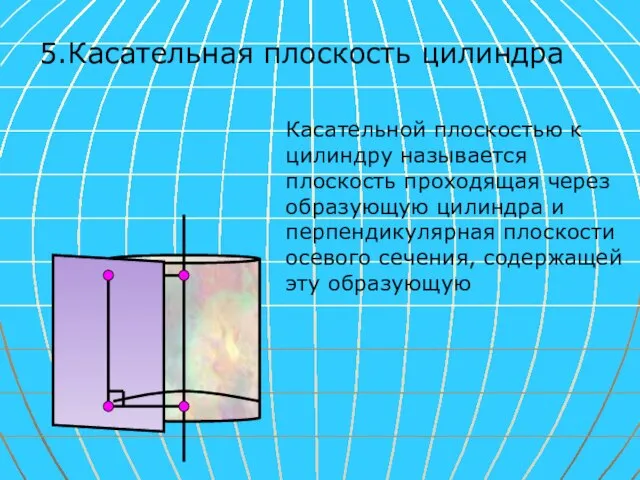
5.Касательная плоскость цилиндра
Касательной плоскостью к цилиндру называется плоскость проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую

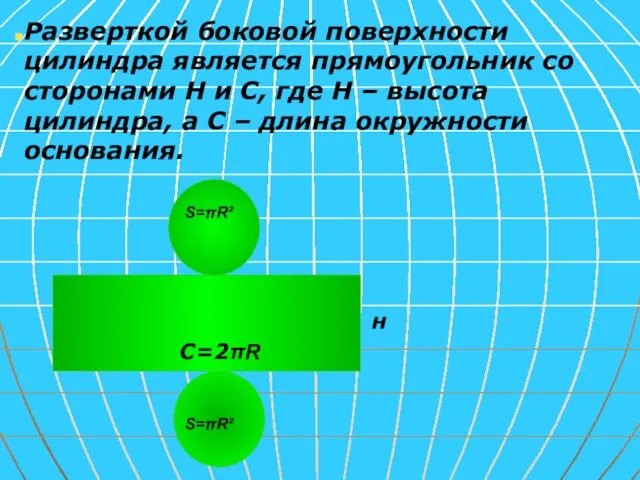
Разверткой боковой поверхности цилиндра является прямоугольник со сторонами Н и С, где Н – высота цилиндра, а С – длина окружности основания.
н
С=2πR
S=πR²
S=πR²

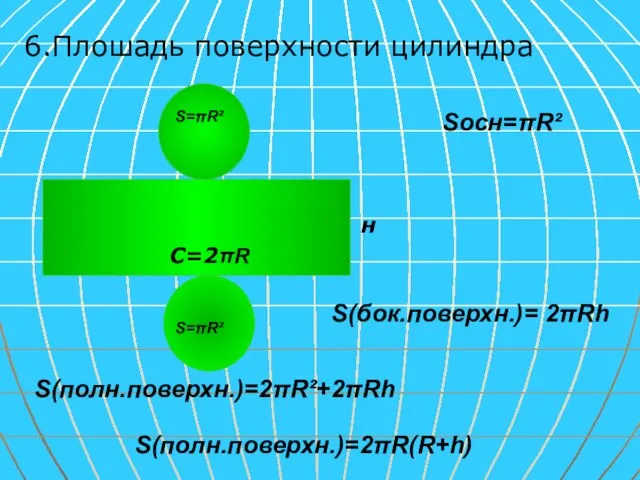
6.Плошадь поверхности цилиндра
S(полн.поверхн.)=2πR(R+h)
S(бок.поверхн.)= 2πRh
Sосн=πR²
н
С=2πR
S=πR²
S=πR²
S(полн.поверхн.)=2πR²+2πRh

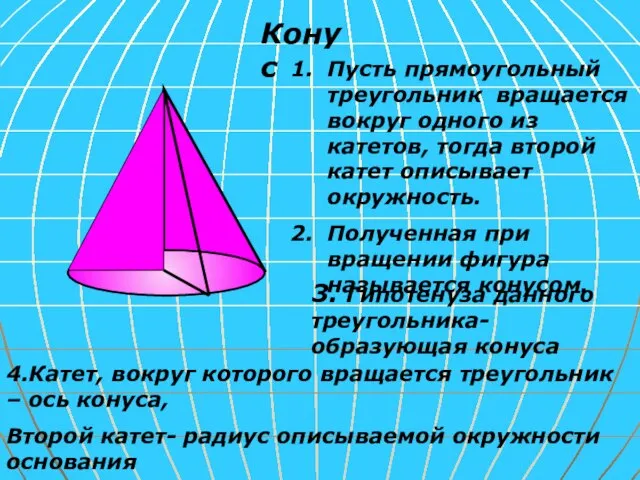
Конус
Пусть прямоугольный треугольник вращается вокруг одного из катетов, тогда второй катет описывает окружность.
Полученная при вращении фигура называется конусом.
3. Гипотенуза данного треугольника-образующая конуса
4.Катет, вокруг которого вращается треугольник – ось конуса,
Второй катет- радиус описываемой окружности основания

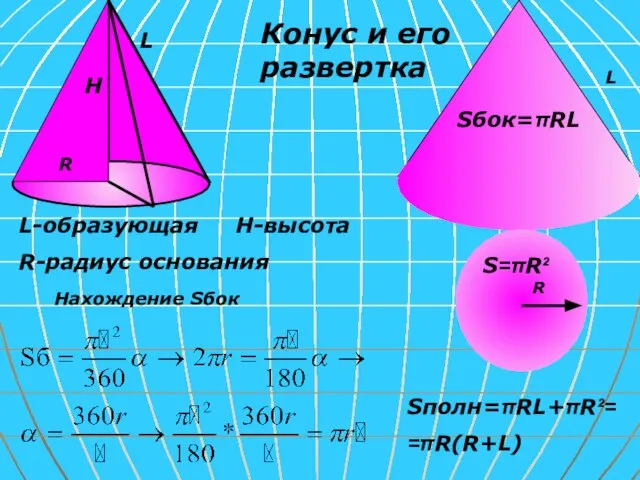
Конус и его развертка
L
H
R
L-образующая H-высота
R-радиус основания
L
R
Sбок=πRL
S=πR²
Нахождение Sбок
Sполн=πRL+πR²=
=πR(R+L)

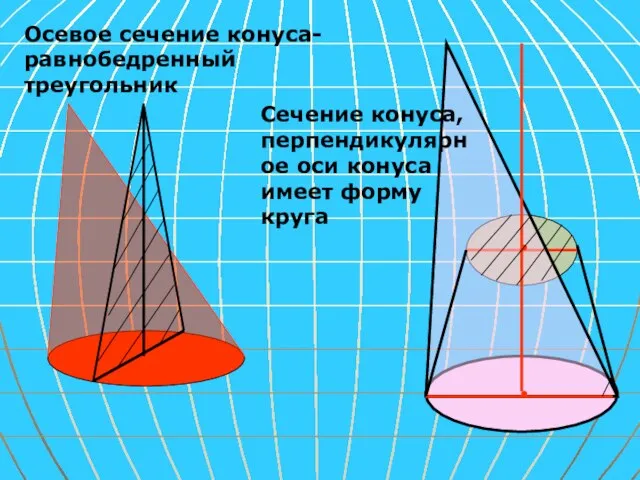
Осевое сечение конуса-равнобедренный треугольник
Сечение конуса, перпендикулярное оси конуса имеет форму круга

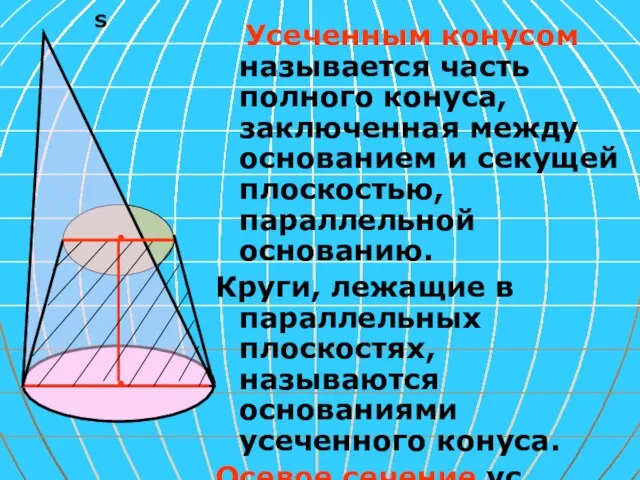
S
Усеченным конусом называется часть полного конуса, заключенная между основанием и секущей плоскостью,параллельной основанию.
Круги, лежащие в параллельных плоскостях, называются основаниями усеченного конуса.
Осевое сечение ус. конуса-
-равнобедренная трапеция

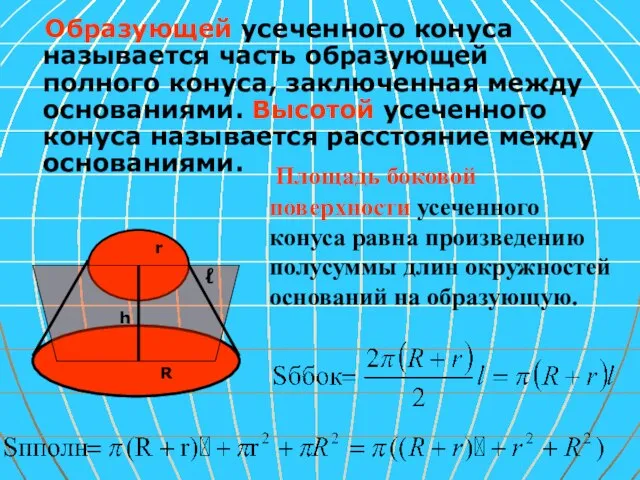
Образующей усеченного конуса называется часть образующей полного конуса, заключенная между основаниями. Высотой усеченного конуса называется расстояние между основаниями.
ℓ
h
R
r
Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.

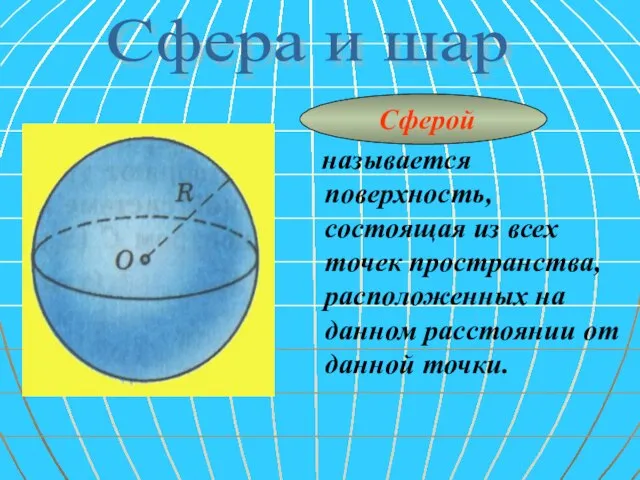
Сферой
называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
Сфера и шар

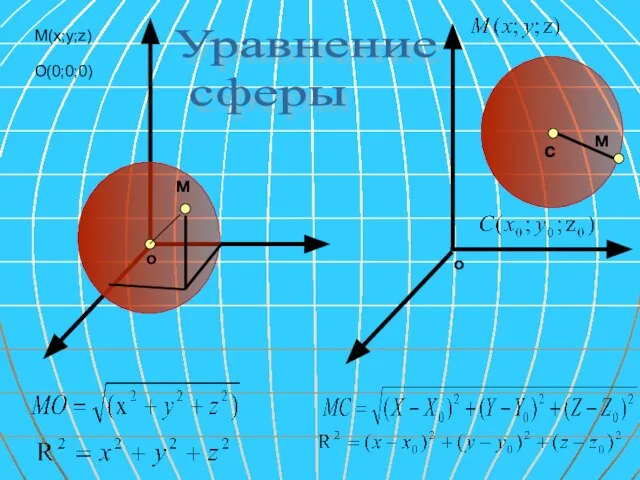
о
о
м
м
с
О(0;0;0)
M(x;y;z)
Уравнение сферы

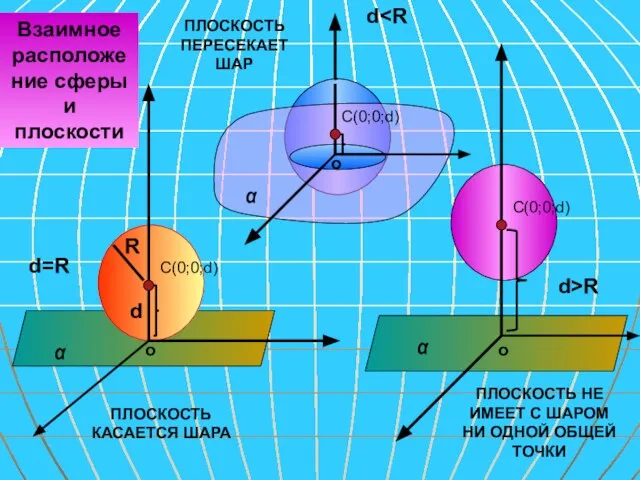
d>R
d=R
d
α
α
α
ПЛОСКОСТЬ КАСАЕТСЯ ШАРА
ПЛОСКОСТЬ НЕ ИМЕЕТ С ШАРОМ НИ ОДНОЙ ОБЩЕЙ ТОЧКИ
ПЛОСКОСТЬ ПЕРЕСЕКАЕТ ШАР
о
о
о
С(0;0;d)
С(0;0;d)
С(0;0;d)
R
d
Взаимное расположение сферы и плоскости

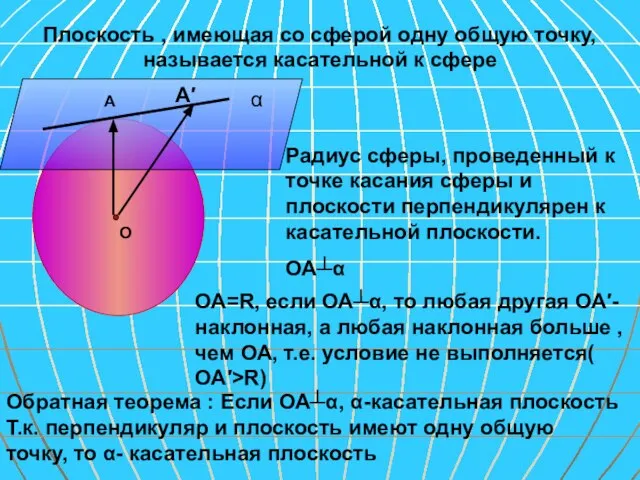
О
А
α
Плоскость , имеющая со сферой одну общую точку, называется касательной к сфере
Радиус сферы, проведенный к точке касания сферы и плоскости перпендикулярен к касательной плоскости.
ОА┴α
А′
ОА=R, если ОА┴α, то любая другая ОА′- наклонная, а любая наклонная больше , чем ОА, т.е. условие не выполняется( ОА′>R)
Обратная теорема : Если ОА┴α, α-касательная плоскость
Т.к. перпендикуляр и плоскость имеют одну общую точку, то α- касательная плоскость

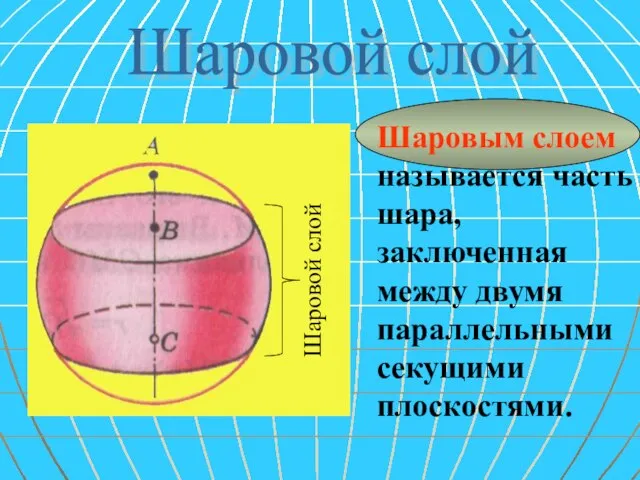
Шаровой слой
Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями.

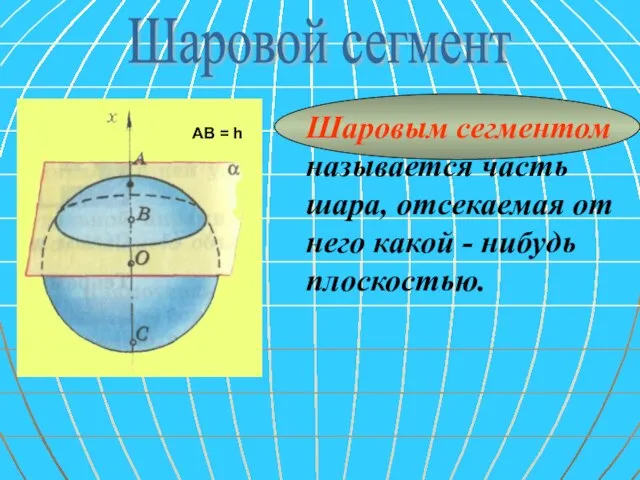
Шаровой сегмент
Шаровым сегментом называется часть шара, отсекаемая от него какой - нибудь плоскостью.