Содержание
- 2. План урока Понятие ломаной. Длина ломаной Понятие многоугольника Выпуклые и невыпуклые многоуголь-ники Сумма углов многоугольника Правильные
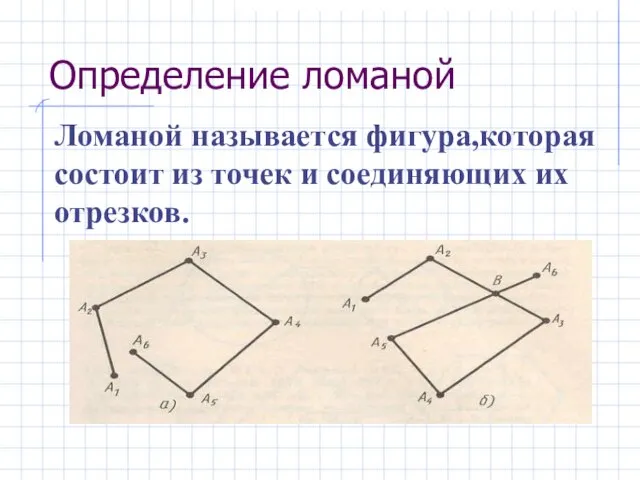
- 3. Определение ломаной Ломаной называется фигура,которая состоит из точек и соединяющих их отрезков.
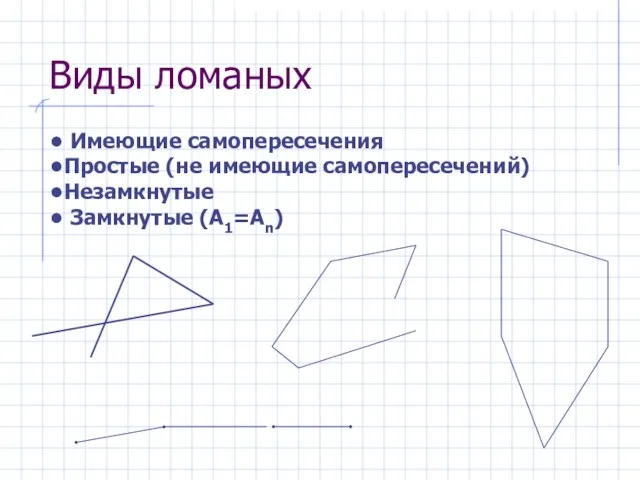
- 4. Виды ломаных Имеющие самопересечения Простые (не имеющие самопересечений) Незамкнутые Замкнутые (А1=Аn)
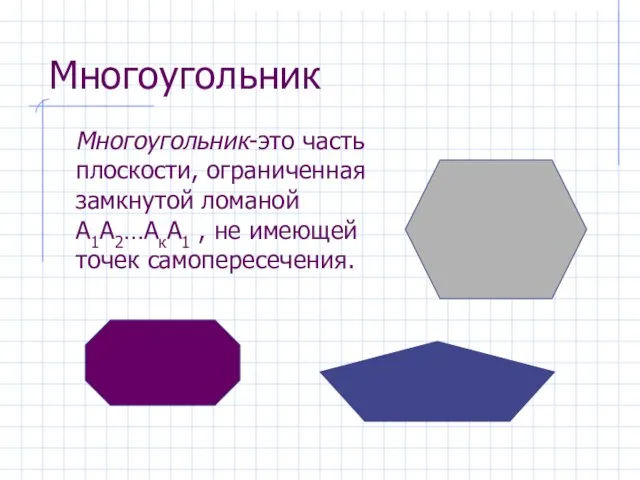
- 5. Многоугольник Многоугольник-это часть плоскости, ограниченная замкнутой ломаной А1А2…АкА1 , не имеющей точек самопересечения.
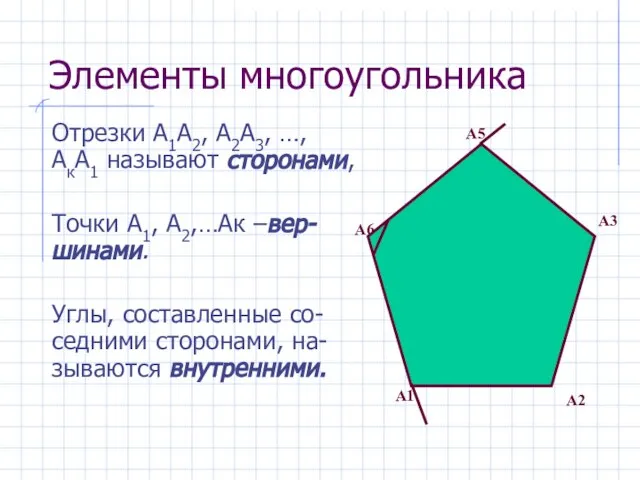
- 6. Отрезки А1А2, А2А3, …, АкА1 называют сторонами, Точки А1, А2,…Ак –вер-шинами. Углы, составленные со-седними сторонами, на-зываются
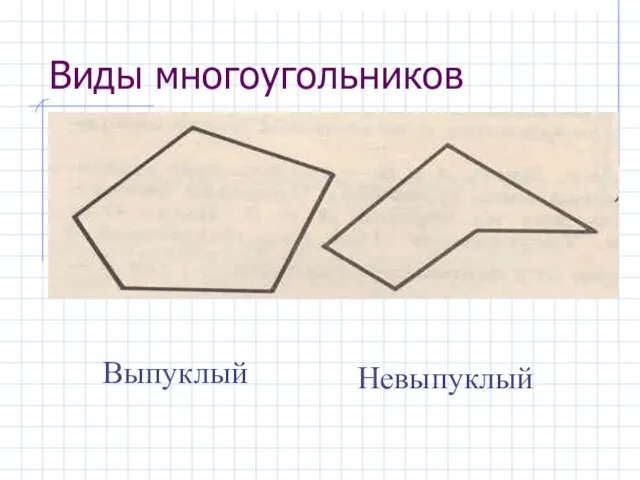
- 7. Виды многоугольников Выпуклый Невыпуклый
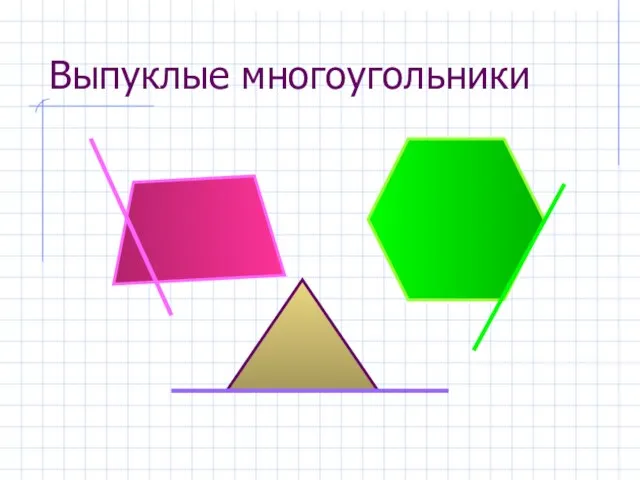
- 8. Выпуклые многоугольники
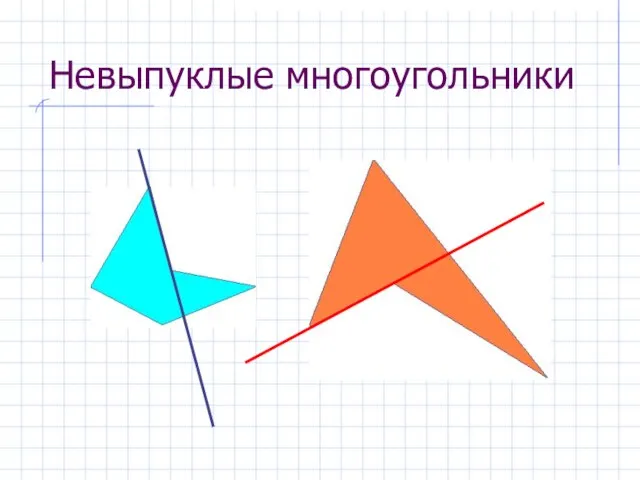
- 9. Невыпуклые многоугольники
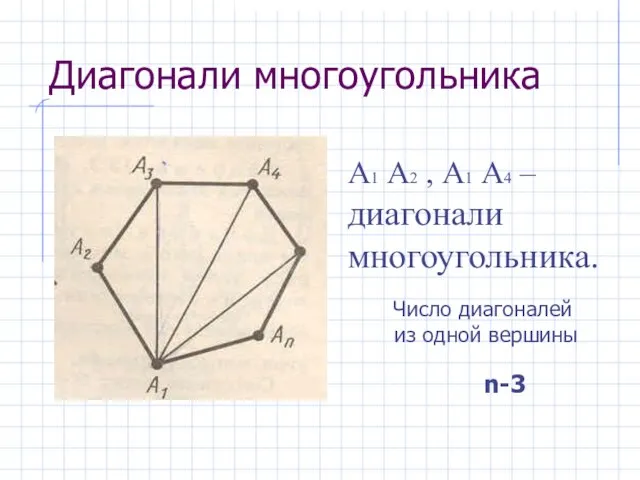
- 10. Диагонали многоугольника А1 А2 , А1 А4 – диагонали многоугольника. Число диагоналей из одной вершины n-3
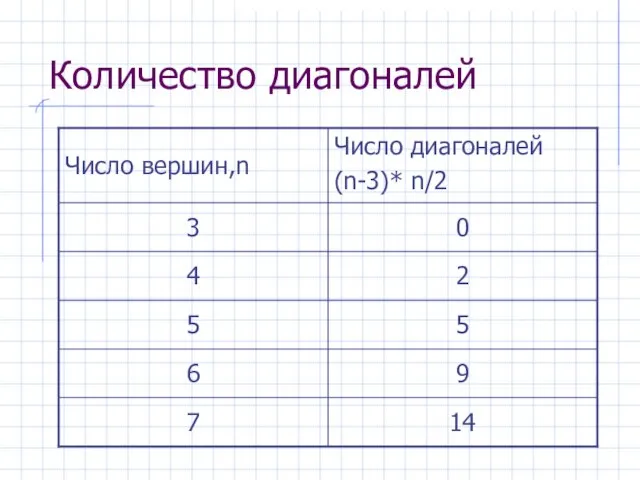
- 11. Количество диагоналей
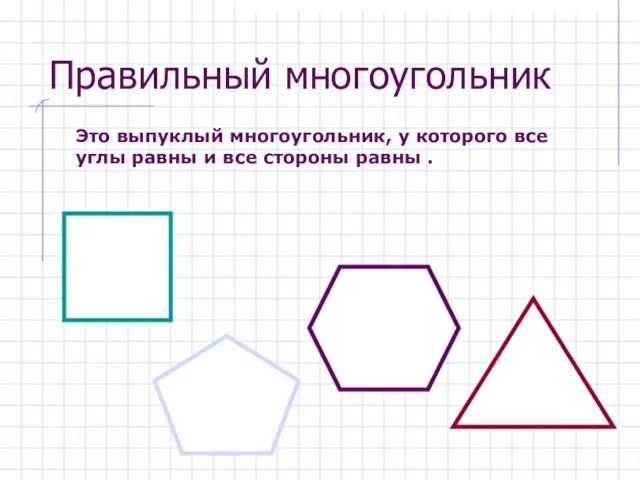
- 12. Правильный многоугольник Это выпуклый многоугольник, у которого все углы равны и все стороны равны .
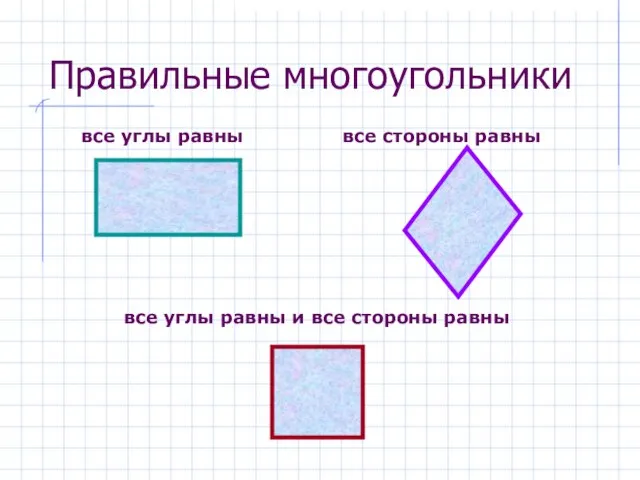
- 13. Правильные многоугольники все углы равны и все стороны равны все углы равны все стороны равны
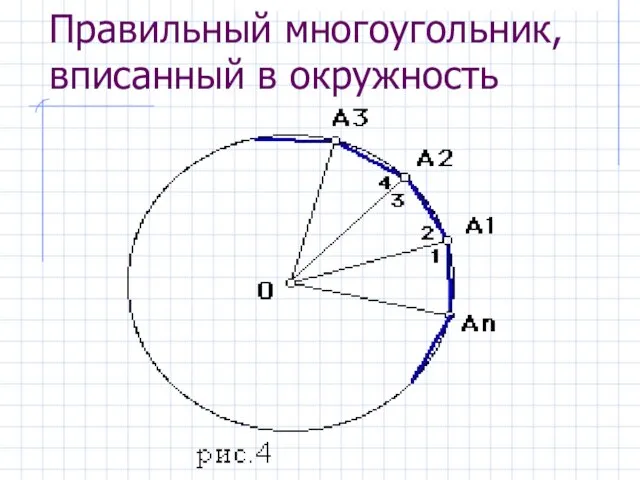
- 14. Правильный многоугольник, вписанный в окружность
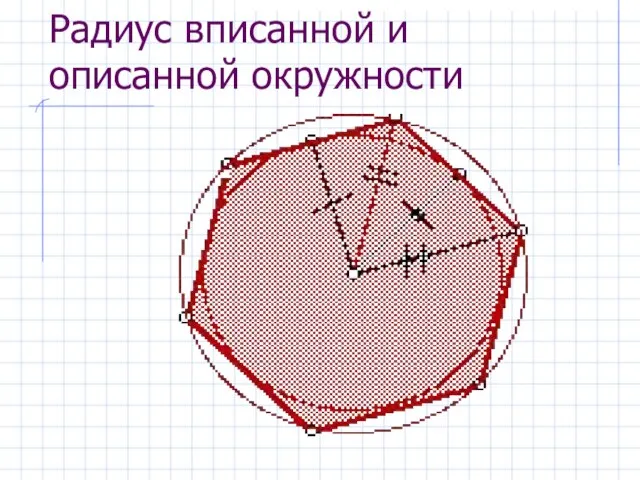
- 15. Радиус вписанной и описанной окружности
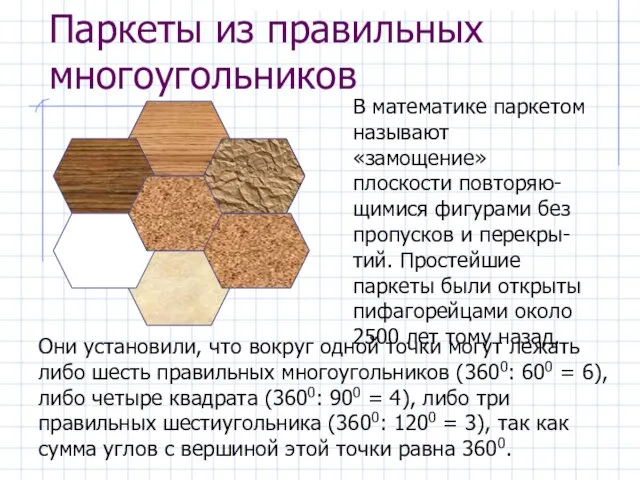
- 16. Паркеты из правильных многоугольников В математике паркетом называют «замощение» плоскости повторяю-щимися фигурами без пропусков и перекры-тий.
- 17. Правильные многоугольники в природе Почему пчелы «выбрали» себе для ячеек на сотах форму правильного шестиугольника? Строя
- 19. Скачать презентацию


 Гидросфера. Внутренние воды
Гидросфера. Внутренние воды LINQ3
LINQ3 Презентация 26
Презентация 26 Защита экрана Digital Care для Теле2
Защита экрана Digital Care для Теле2 Автоматизация в МБЛ (1)
Автоматизация в МБЛ (1) Топливно-энергетический комплекс
Топливно-энергетический комплекс Статистическое наблюдение библиотек Российской Федерации
Статистическое наблюдение библиотек Российской Федерации Презентация на тему БАКТЕРИИ
Презентация на тему БАКТЕРИИ  Страна "Умножения"
Страна "Умножения" Здравствуй Новый год!
Здравствуй Новый год! Cистемно-деятельностный подход - основа стандартов нового поколения
Cистемно-деятельностный подход - основа стандартов нового поколения Объяснение иллюзий
Объяснение иллюзий Познание
Познание 269260
269260 Драматические образы в музыке
Драматические образы в музыке Предпосылки становления индустриальной цивилизации
Предпосылки становления индустриальной цивилизации Секция 3
Секция 3 ЗАО «Теккноу» Санкт-Петербург Московский пр. 212, оф. 4098 (812) 380-06-93
ЗАО «Теккноу» Санкт-Петербург Московский пр. 212, оф. 4098 (812) 380-06-93  УЧИМСЯГОВОРИТЬ
УЧИМСЯГОВОРИТЬ Венецианская маска
Венецианская маска Оқы, еске түсір, айт
Оқы, еске түсір, айт Самый прибыльный бизнес
Самый прибыльный бизнес Бумага – самое ценное изобретение человечества
Бумага – самое ценное изобретение человечества Наша родина Россия
Наша родина Россия Хоть поверьте - хоть проверьте
Хоть поверьте - хоть проверьте Наставление человечеству. Нургисаева А
Наставление человечеству. Нургисаева А Устье-Угольская школа
Устье-Угольская школа