Геометрия 7 класс

Данная презентация предназначена для проведения обобщающего урока по курсу геометрии 7 класс.
Продолжительность показа презентации зависит от степени подготовки класса: от 3 до 4 уроков.
Отдельные фрагменты презентации можно использовать как при объяснении нового материала, так и при закреплении или повторении.
далее

Аксиомы
Точки и прямые
Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и точки не принадлежащие ей.
А
В
В

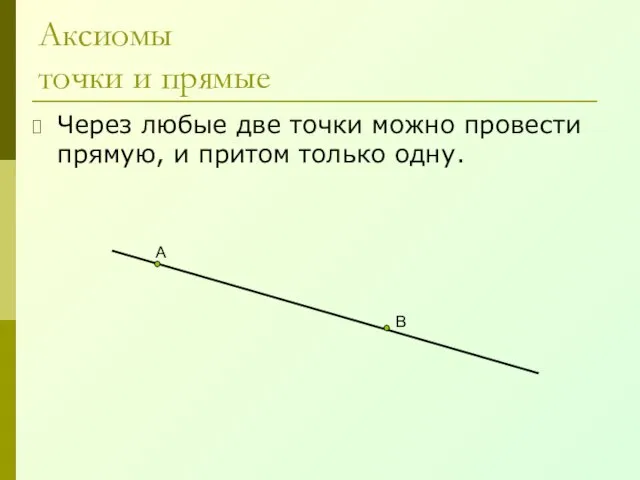
Аксиомы
точки и прямые
Через любые две точки можно провести прямую, и притом только одну.
А
В

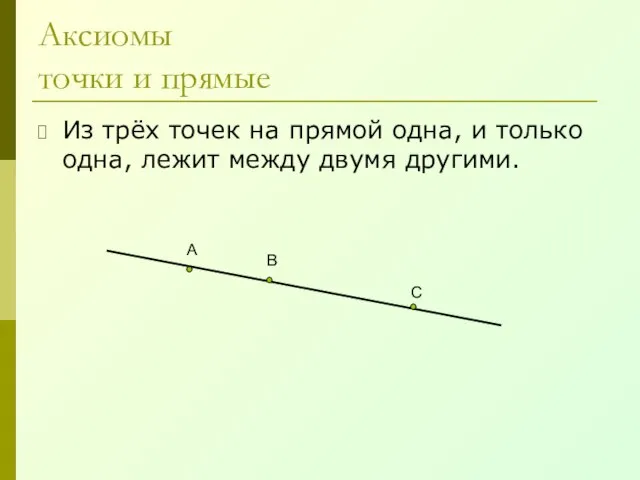
Аксиомы
точки и прямые
Из трёх точек на прямой одна, и только одна, лежит между двумя другими.
А
В
С

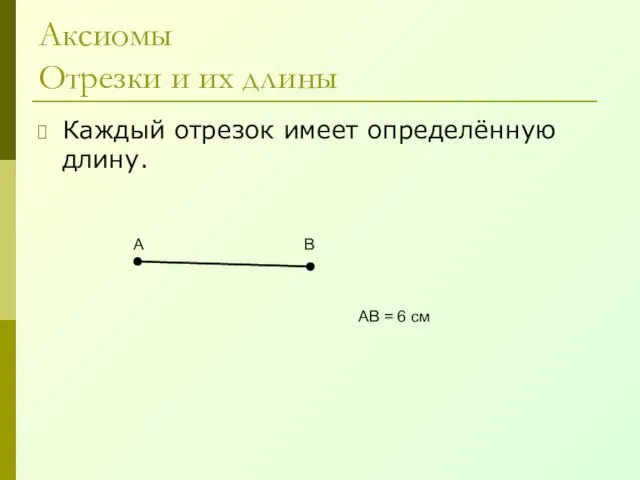
Аксиомы
Отрезки и их длины
Каждый отрезок имеет определённую длину.
А
В
АВ = 6 см

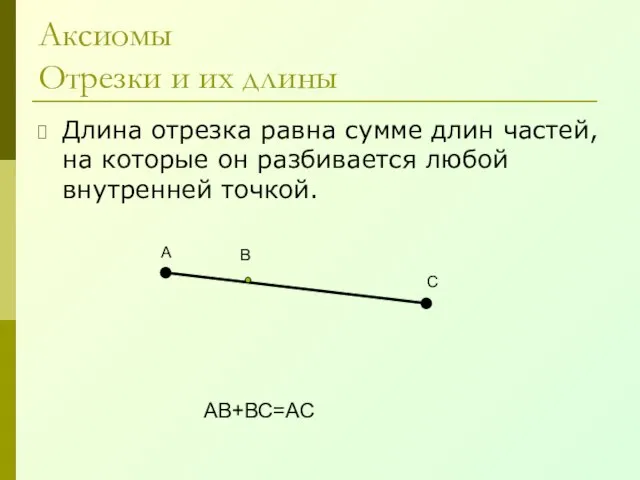
Аксиомы
Отрезки и их длины
Длина отрезка равна сумме длин частей, на которые он разбивается любой внутренней точкой.
В
А
С
АВ+ВС=АС

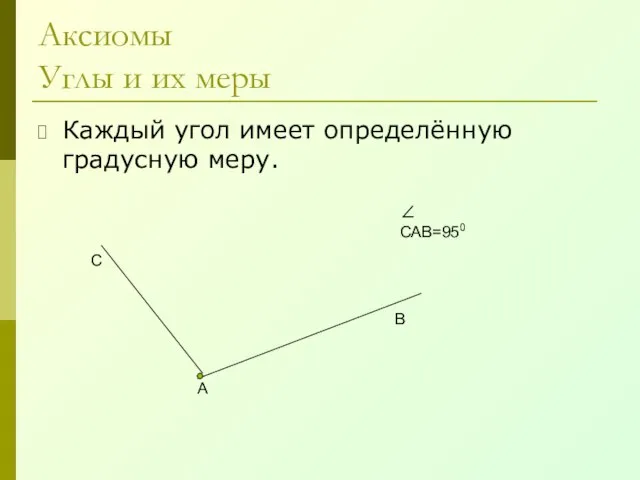
Аксиомы
Углы и их меры
Каждый угол имеет определённую градусную меру.
А
В
С
∠ САВ=950

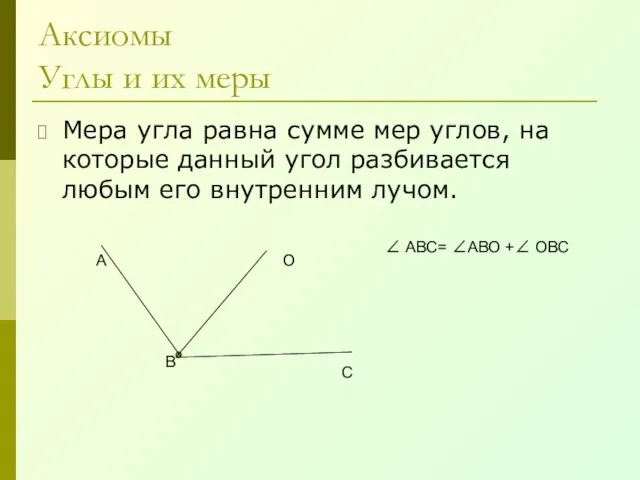
Аксиомы
Углы и их меры
Мера угла равна сумме мер углов, на которые данный угол разбивается любым его внутренним лучом.
А
В
С
О
∠ АВС= ∠АВО +∠ ОВС

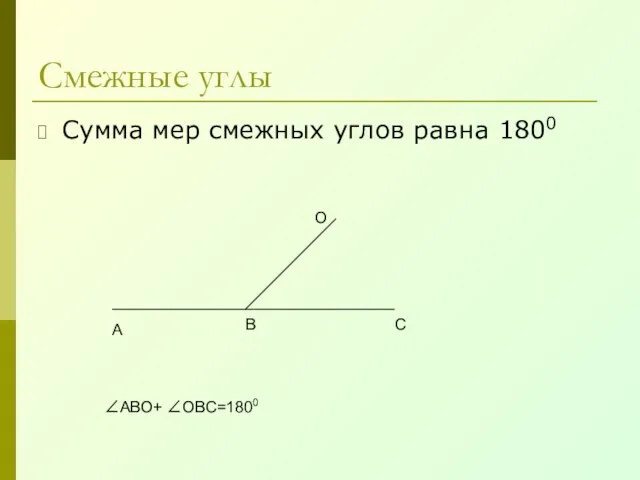
Смежные углы
Сумма мер смежных углов равна 1800
А
В
С
О
∠АВО+ ∠ОВС=1800

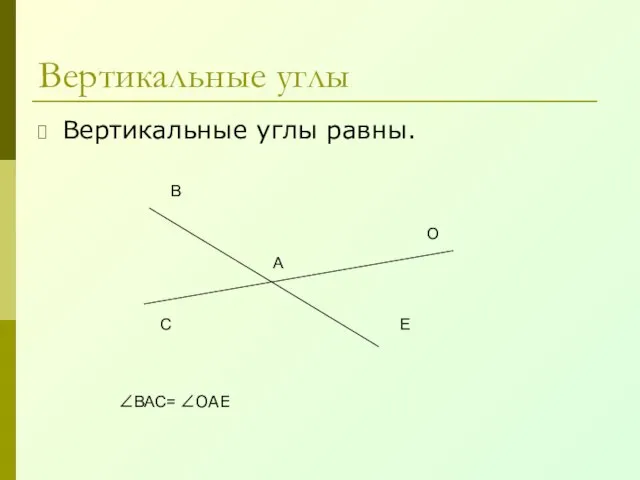
Вертикальные углы
Вертикальные углы равны.
А
В
С
О
Е
∠ВАС= ∠ОАЕ

Параллельные прямые
определение
Прямые называются параллельными, если
-они лежат в одной плоскости
-они не пересекаются
а
в
а⏐⏐в

Параллельные прямые
Признаки
Если две прямые с поперечиной образуют равные накрест лежащие углы, то прямые параллельны
1
2
3
4
а
в
∠2=∠3⇒ а⏐⏐в
Если две прямые параллельны, то они
с поперечиной образуют равные накрест лежащие углы
а⏐⏐в ⇒ ∠2=∠3
Параллельные прямые
Свойства

Параллельные прямые
Признаки
Если сумма внутренних односторонних углов равна 1800 ,то прямые параллельны
1
2
3
4
а
в
∠2+∠4=1800 ⇒а⏐⏐в
Если сумма внутренних односторонних углов равна 1800 ,то прямые параллельны
Если прямые параллельны, то сумма внутренних односторонних углов равна 1800
а⏐⏐в ⇒∠2+∠4=1800
Параллельные прямые
Свойства

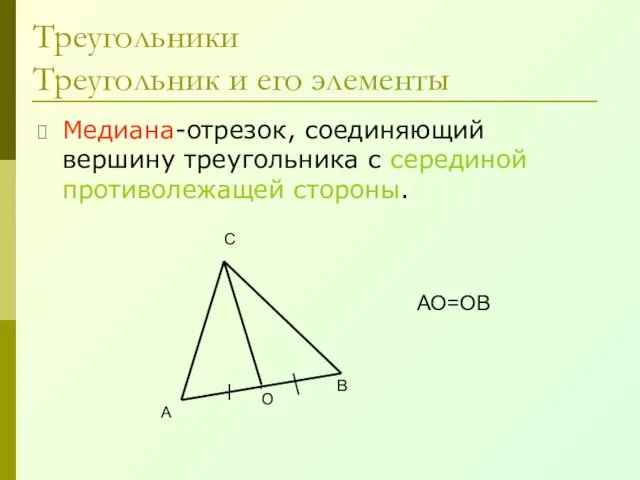
Треугольники
Треугольник и его элементы
Медиана-отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
А
В
С
О
АО=ОВ

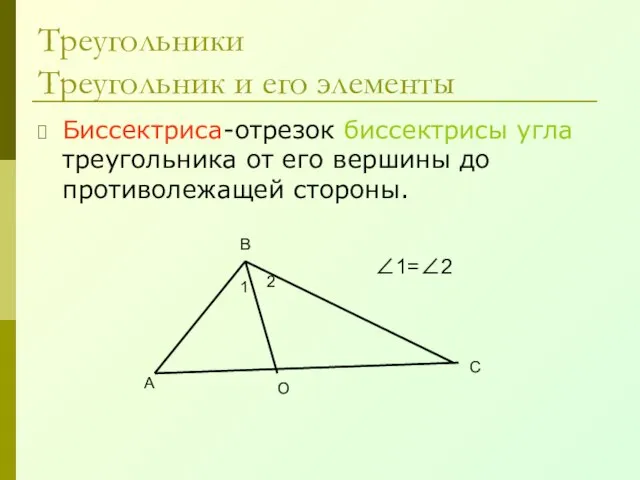
Биссектриса-отрезок биссектрисы угла треугольника от его вершины до противолежащей стороны.
Треугольники
Треугольник и его элементы
А
В
С
О
1
2
∠1=∠2

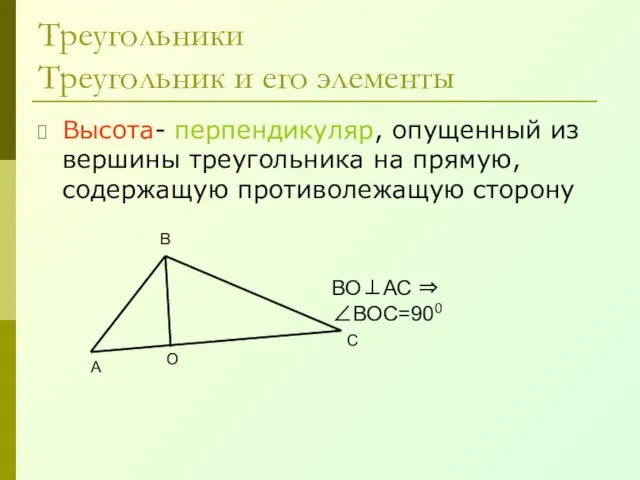
Треугольники
Треугольник и его элементы
Высота- перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону
А
В
С
О
ВО⊥АС ⇒ ∠ВОС=900

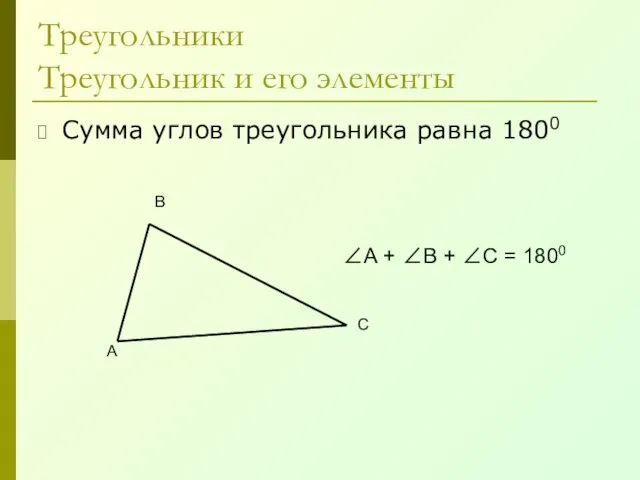
Треугольники
Треугольник и его элементы
Сумма углов треугольника равна 1800
А
В
С
∠А + ∠В + ∠С = 1800

Треугольники
Треугольник и его элементы
Угол, смежный с углом треугольника, называют внешним углом.
.
А
В
С
О
1
∠ВСО=∠1-внешний
∠1=∠А+∠В
Внешний угол треугольника равен
сумме двух внутренних , не смежных с ним

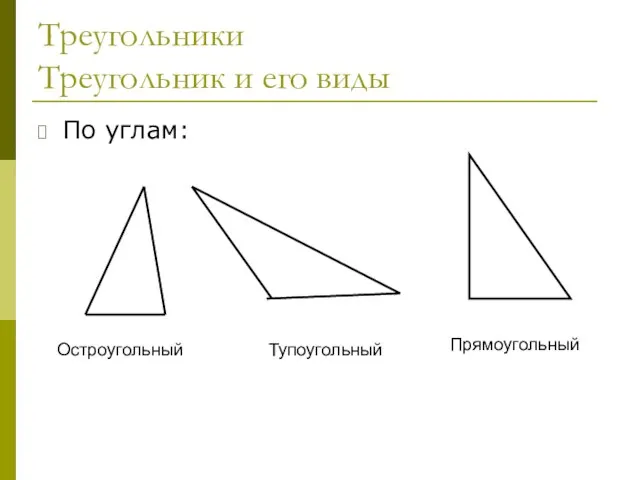
Треугольники
Треугольник и его виды
По углам:
Остроугольный
Тупоугольный
Прямоугольный

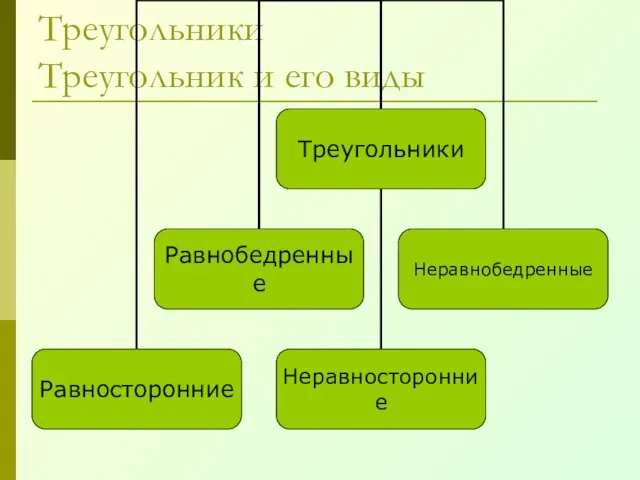
Треугольники
Треугольник и его виды

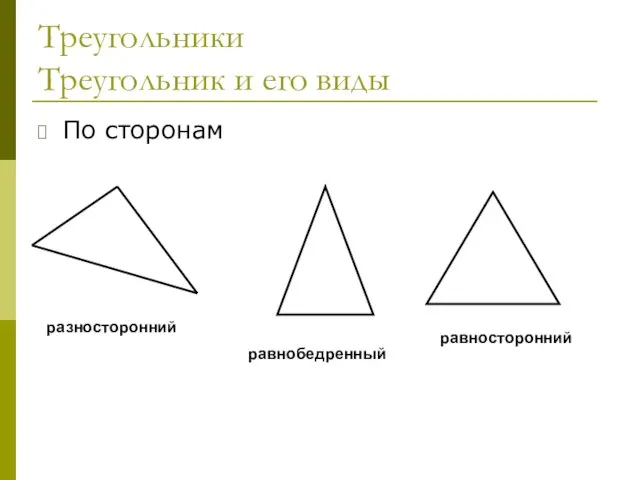
Треугольники
Треугольник и его виды
По сторонам
разносторонний
равнобедренный
равносторонний

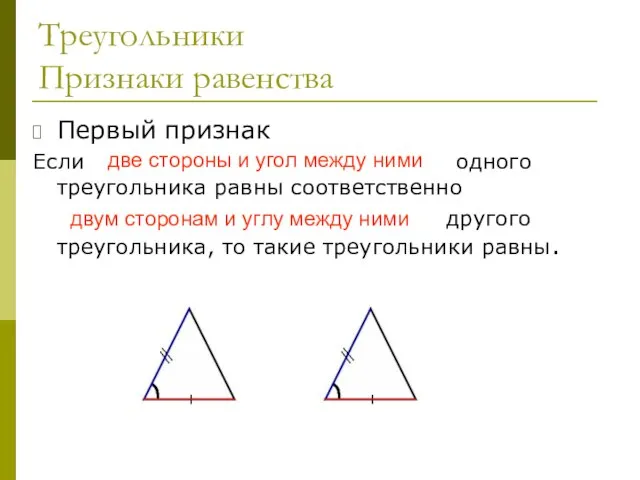
Треугольники
Признаки равенства
Первый признак
Если две стороны и угол между ними одного треугольника равны соответственно
двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
две стороны и угол между ними
двум сторонам и углу между ними

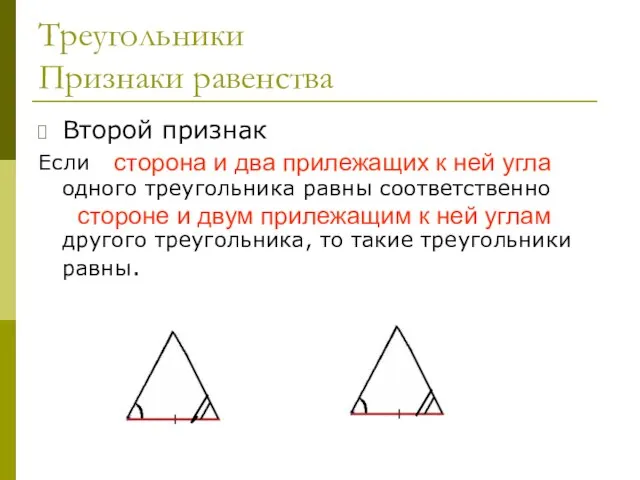
Треугольники
Признаки равенства
Второй признак
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
сторона и два прилежащих к ней угла
стороне и двум прилежащим к ней углам

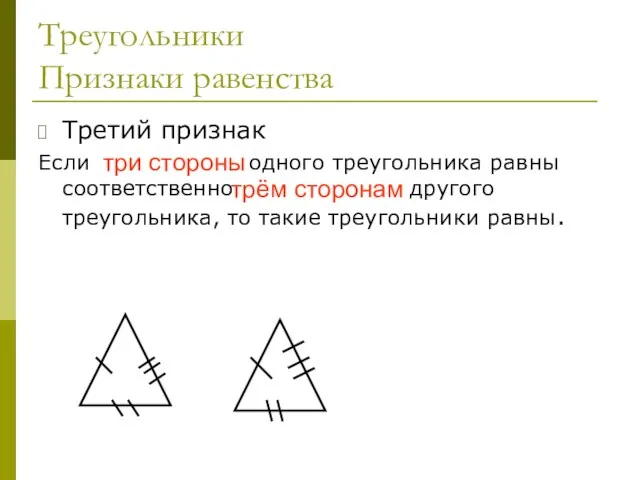
Треугольники
Признаки равенства
Третий признак
Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны.
три стороны
трём сторонам

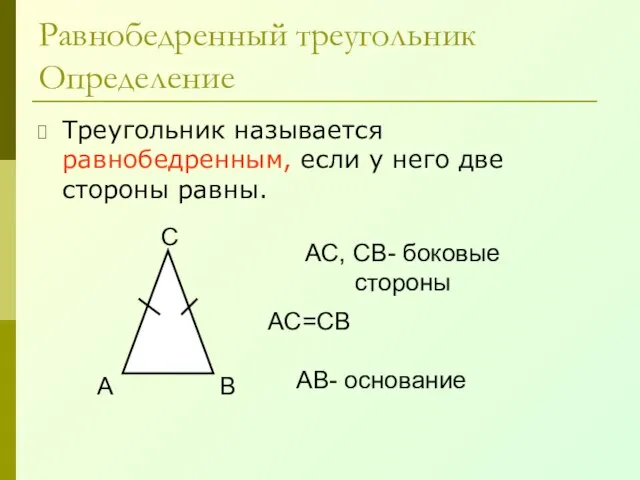
Равнобедренный треугольник
Определение
Треугольник называется равнобедренным, если у него две стороны равны.
А
В
С
АС, СВ- боковые стороны
АС=СВ
АВ- основание

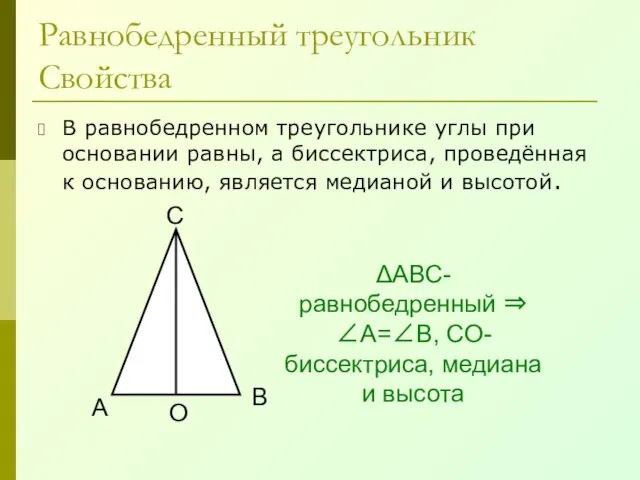
Равнобедренный треугольник
Свойства
В равнобедренном треугольнике углы при основании равны, а биссектриса, проведённая к основанию, является медианой и высотой.
А
В
С
О
ΔАВС- равнобедренный ⇒ ∠А=∠В, СО- биссектриса, медиана и высота

Равнобедренный треугольник
Признаки
Если в треугольнике два угла равны, то он равнобедренный.
Если в треугольнике медиана является высотой, то он равнобедренный.
Если в треугольнике медиана является биссектрисой, то он равнобедренный.
Если в треугольнике высота является биссектрисой, то он равнобедренный

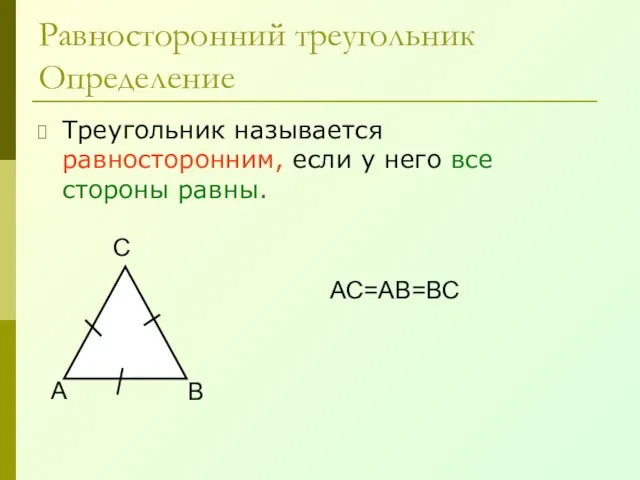
Равносторонний треугольник
Определение
Треугольник называется равносторонним, если у него все стороны равны.
А
В
С
АС=АВ=ВС

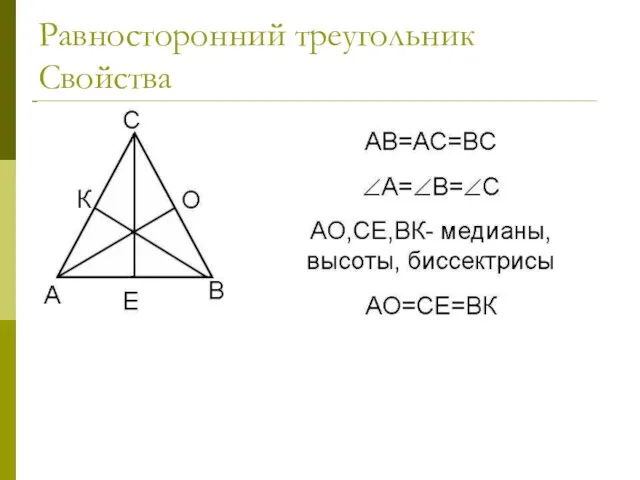
Равносторонний треугольник
Свойства
В равностороннем треугольнике все углы равны.
В равностороннем треугольнике каждая биссектриса является медианой и высотой.
В равностороннем треугольнике все три медианы равны.

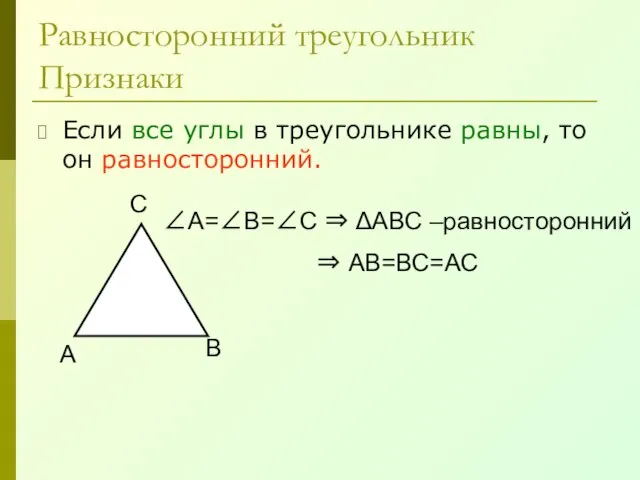
Равносторонний треугольник
Признаки
Если все углы в треугольнике равны, то он равносторонний.
А
В
С
∠А=∠В=∠С ⇒ ΔАВС –равносторонний
⇒ АВ=ВС=АС

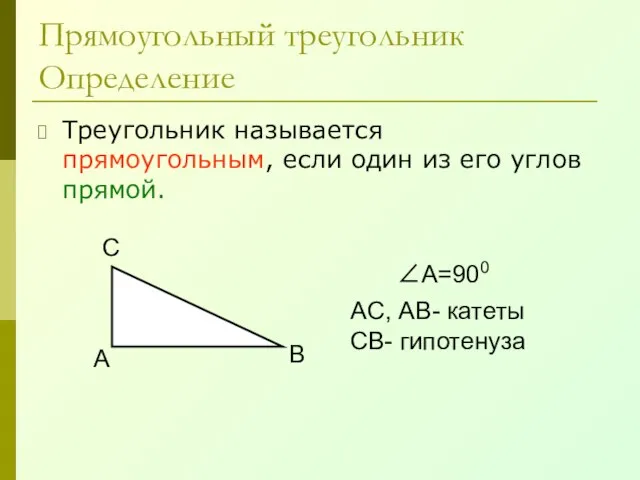
Прямоугольный треугольник
Определение
Треугольник называется прямоугольным, если один из его углов прямой.
А
В
С
∠А=900
АС, АВ- катеты
СВ- гипотенуза

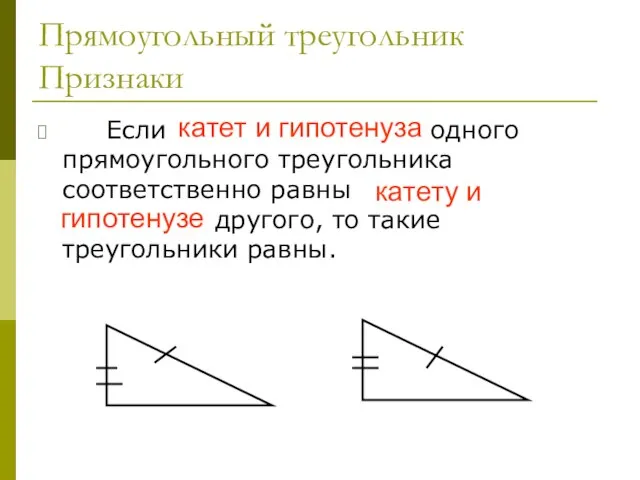
Прямоугольный треугольник
Признаки
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого, то такие треугольники равны.
катет и гипотенуза
катету и
гипотенузе

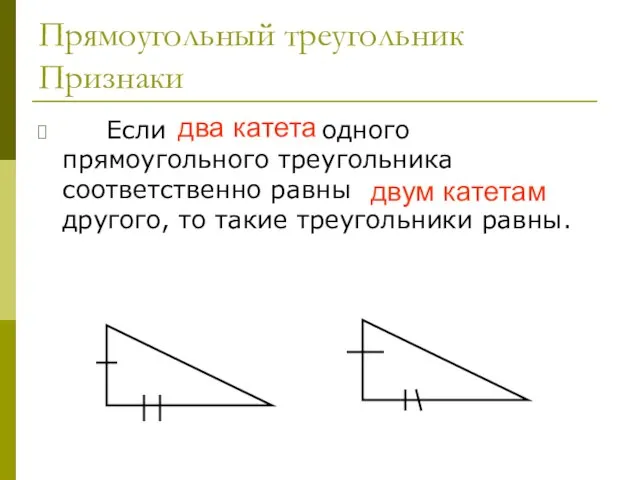
Прямоугольный треугольник
Признаки
Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого, то такие треугольники равны.
два катета
двум катетам

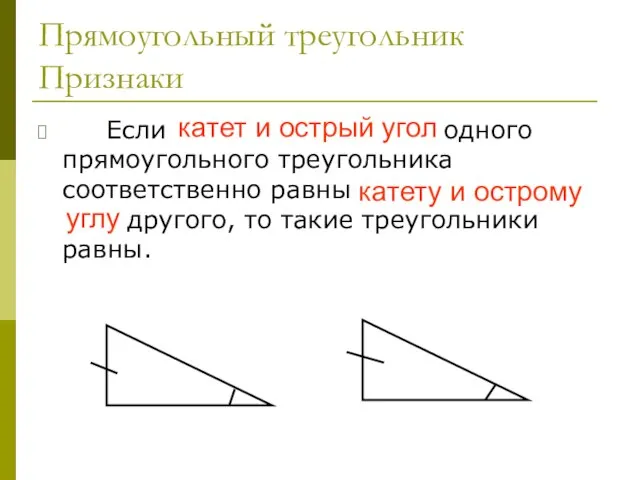
Прямоугольный треугольник
Признаки
Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого, то такие треугольники равны.
катет и острый угол
катету и острому
углу

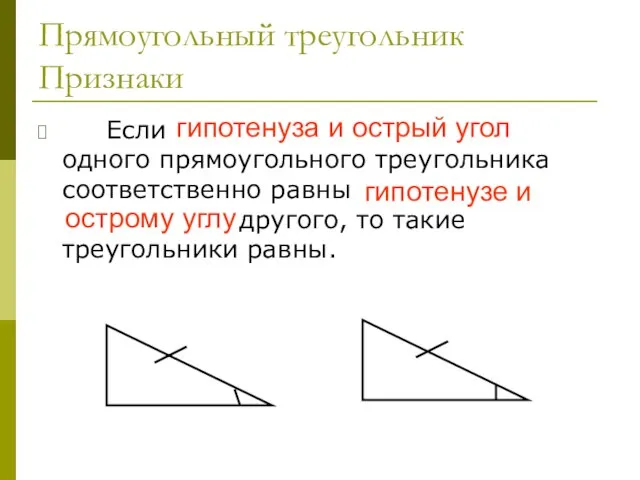
Прямоугольный треугольник
Признаки
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
гипотенуза и острый угол
гипотенузе и
острому углу

Прямоугольный треугольник
Свойства
Катет прямоугольного треугольника, лежащий против угла 300, равен половине гипотенузы.
А
С
В
∠А=900
∠В=300
АС=0,5ВС