Геометрия на вольном воздухе

Жители Древнего Египта задались вопросом: «Как найти высоту одной из громадных пирамид?» Фалес нашёл решение этой задачи. Он воткнул длинную палку вертикально в землю и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды.»

В нашем учебнике геометрии описан способ для нахождения высоты предмета.
Если нужно определить высоту какого-нибудь предмета, например высоту телеграфного столба А1С1, изображённого на рисунке, поставим на некотором
расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку А1 столба. Отметим на поверхности земли точку В, в которой прямая А1А пересекается с поверхностью земли. Прямоугольные треугольники А1С1В и АСВ подобны по первому признаку подобия треугольников.
Измерив расстояние ВС1 и ВС и зная длину АС шеста, определяем высоту А1С1 телеграфного столба.

При изучении научных материалов можно убедиться, что подобие треугольников можно применять не только на уроках геометрии, но и на практике при измерении расстояний и высоты предметов.
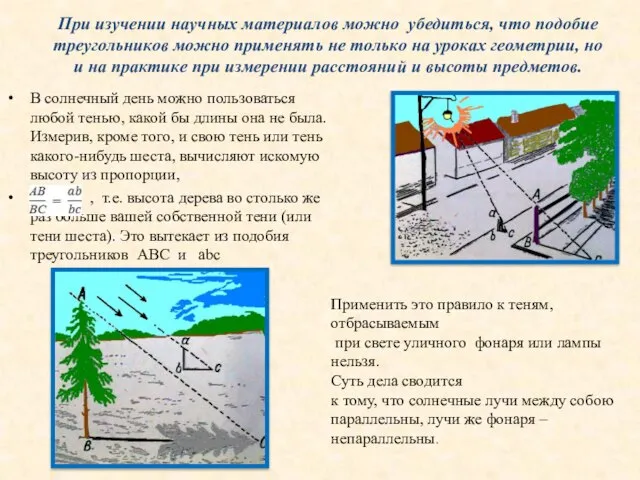
В солнечный день можно пользоваться любой тенью, какой бы длины она не была. Измерив, кроме того, и свою тень или тень какого-нибудь шеста, вычисляют искомую высоту из пропорции,
, т.е. высота дерева во столько же раз больше вашей собственной тени (или тени шеста). Это вытекает из подобия треугольников ABC и abc
Применить это правило к теням, отбрасываемым
при свете уличного фонаря или лампы нельзя.
Суть дела сводится
к тому, что солнечные лучи между собою
параллельны, лучи же фонаря – непараллельны.

По способу Жюля Верна.
- Да. И следовательно, если мы измерим два первых расстояния, то зная высоту шеста, сможем вычислить четвертый, неизвестный член пропорции, т. е. высоту стены. Мы обойдемся, таким образом, без непосредственного измерения этой высоты.
Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее – 500 футам. По окончании измерений инженер составил следующую запись:
15 : 500 = 10 : х,
500 х 10 = 5000
5000 : 15 = 333,3. Значит, высота гранитной стены равнялась 333 футам.
Взяв прямой шест, футов 12 длиною, инженер
измерил его возможно точнее, сравнивая со своим
ростом, который был хорошо ему известен. Герберт
же нес за ним отвес, врученный ему инженером:
просто камень, привязанный к концу веревки.
Не доходя футов 500 до гранитной стены,
поднимавшейся отвесно, инженер воткнул шест
фута на два в песок и, прочно укрепив его,
поставил вертикально с помощью отвеса.

Как поступил сержант.
Затем, не меняя положения головы, смотрите по направлению горизонтальной прямой аС, замечая точки с и С, в которых луч зрения встречает шест и ствол. Попросите помощника сделать в этих местах пометки, и наблюдение окончено. Остается только на основании подобия треугольников аbс и аВС вычислить ВС из пропорции ВС : вс = аС : ас, откуда
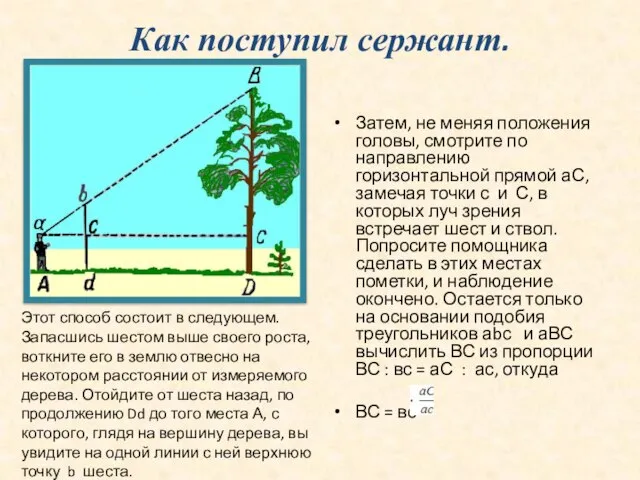
ВС = вс
Этот способ состоит в следующем.
Запасшись шестом выше своего роста, воткните его в землю отвесно на некотором расстоянии от измеряемого дерева. Отойдите от шеста назад, по продолжению Dd до того места А, с которого, глядя на вершину дерева, вы увидите на одной линии с ней верхнюю точку b шеста.

Не приближаясь к дереву.
Вот и весь прибор. Чтобы измерить им высоту, держат его в руках, направив планку cd вертикально (для чего при ней имеется отвес- шнурок с грузиком), и становятся последовательно в двух местах: сначала в точка А, где располагают прибор концом с вверх, а затем в точке А1, подальше, где прибор держат вверх концом d. Точка А избирается так, чтобы глядя из a на конец с, видеть его на одной прямой с верхушкой дерева. Точку А1 отыскивают так, чтобы, глядя из a1 на точку d1, видеть ее совпадающей с В. В отыскании этих двух точек А и А1 заключается все измерение, потому что искомая часть высоты дерева ВС равна расстоянию АА1. Равенство вытекает, как легко сообразить, из того, что a= ВС, а a1С = 2ВС; значит, a1С – aС = ВС.
Случается, что почему-либо неудобно
подойти вплотную к основанию измеряемого
дерева. Можно ли в таком случае определить высоту ?
Вполне возможно. Для этого придуман остроумный прибор, который легко изготовить самому. Две планки ab и cd скрепляются под прямым углом так, чтобы ab
равнялось bc, а bd составляло половину ab.

Высотомер лесорубов
Сущность прибора видна на рисунке. Картонный или деревянный прямоугольник abcd держат в руках так, чтобы, глядя вдоль края ab, видеть на одной линии с ним вершиеу В дерева. В точке b привешен на нити грузик q. Замечают точку n, в которой нить пересекает линию dc. Треугольники bBC и bnc подобны, так как оба прямоугольные и имеют равные острые углы bBC и bnc (с соответственно параллельными сторонами). Значит, мы в праве записать пропорцию ВС : nc = bC :bc;
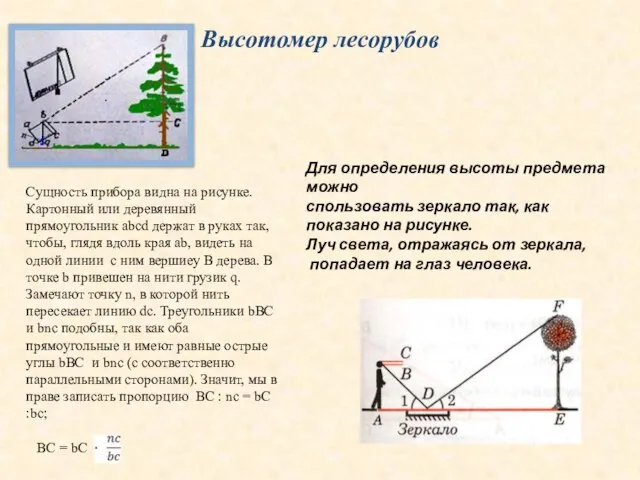
BC = bC
Для определения высоты предмета можно
спользовать зеркало так, как показано на рисунке.
Луч света, отражаясь от зеркала,
попадает на глаз человека.

При помощи зеркала
В точке С кладут горизонтально зеркальце
и отходят от него назад в такую точку D,
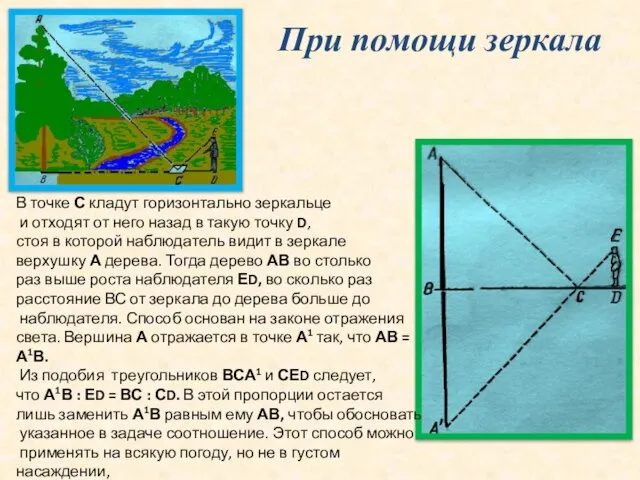
стоя в которой наблюдатель видит в зеркале
верхушку А дерева. Тогда дерево АВ во столько
раз выше роста наблюдателя ЕD, во сколько раз
расстояние ВС от зеркала до дерева больше до
наблюдателя. Способ основан на законе отражения
света. Вершина А отражается в точке А1 так, что АВ = А1В.
Из подобия треугольников ВСА1 и СЕD следует,
что А1В : ЕD = ВС : СD. В этой пропорции остается
лишь заменить А1В равным ему АВ, чтобы обосновать
указанное в задаче соотношение. Этот способ можно
применять на всякую погоду, но не в густом насаждении,
а к одиноко стоящему дереву.

Две сосны
В 40 м одна от другой растут две сосны. Вы измерили их высоту: одна 32м высоты, другая, молодая – всего 6 м.
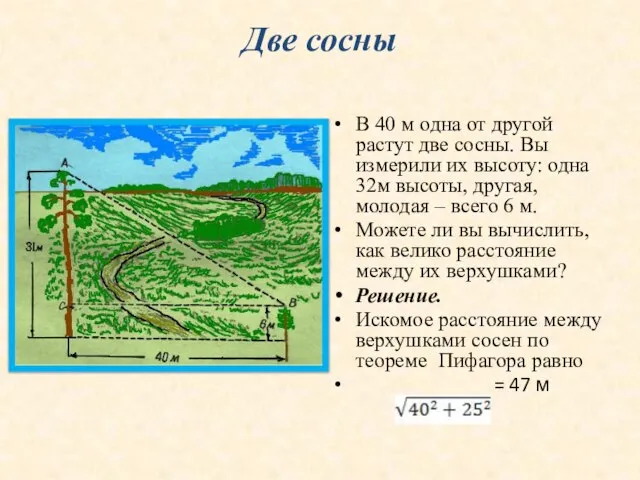
Можете ли вы вычислить, как велико расстояние между их верхушками?
Решение.
Искомое расстояние между верхушками сосен по теореме Пифагора равно
= 47 м

Объем и вес тела на корню.
Для этого понадобиться четыре измерения – длины ствола и трех поперечников: нижнего сруба, верхнего и посередине длины. Измерение нижнего и верхнего поперечников очень просто; непосредственное же определение среднего поперечника без специального приспособления довольно неудобно. Но трудность можно обойти, если измерить бечевкой окружность ствола и разделить на число , то модно получить диаметр.
Все это, однако, совершенно неприменимо к дереву на корню; если не взбираться на него, то измерению доступен только диаметр его нижней части. В этом случае придется для определения объема довольствоваться лишь весьма приближенной оценкой, утешаясь тем, что и профессиональные лесоводы поступают обычно сходным же образом. Они пользуются для этого таблицей так называемых «видовых чисел», т.е. чисел, которые показывают, какую долю объем измеряемого дерева составляет от объема цилиндра той же высоты и диаметра, измеренного на высоте груди взрослого человека, т.е. 130 см (на этой высоте его удобнее всего измерить). Конечно, «видовые числа» различны для деревьев разной породы и высоты, так как форма ствола изменчива.

Геометрия листьев.
Геометр может сказать здесь своё слово: он может определить, во сколько раз площадь листа поросли больше площади листа родительского дерева.
Можно определить разными способами, но короткий способ основан на том, что оба листа, различные по величине, имеют все же одинаковую или почти одинаковую форму: другими словами, - это фигуры, геометрически подобные. Площади таких фигур относятся, как квадраты их линейных размеров. Значит, определив, во сколько раз один лист длиннее или шире другого, мы простым возведением этого числа в квадрат узнаем отношение их площадей.

Шестиногие богатыри
«…Оказывается, мускульная сила, по мере того как животное разрастается до двойной длины и восьмерного веса, увеличивается лишь в четыре раза, т.е. животное сделается вдвое слабее. На этом основании животное, которое втрое длиннее (с поперечным сечением в 9 раз обширнейшим и с весом в 27 раз большим), оказывалась бы относительно втрое слабее, а то, которое вчетверо длиннее,- вчетверо слабее и т.д. Законом неодинакового нарастания объема и веса животного, а вместе с тем и мускульной силы объясняется, почему муравьи могут тащить тяжести, в 30, в 40 раз превосходящие вес собственного их тела».
Удивительные создания муравьи! Откуда у насекомого
берется сила, чтобы без видимого напряжения
втаскивать груз в десять раз тяжелее его самого?
Ведь человек не мог бы взбегать по лестнице, держа
на плечах, например, пианино, а отношение веса
груза к весу тела у муравья примерно такое же.
Выходит, что муравей относительно сильнее человека!

Геометрия у реки.
Не переплывая реки, измерить её ширину.
Найдем точку С на продолжении АВ и намечаем при помощи булавочного прибора прямую CD под прямым углом к СА. На прямой CD отмеряем равные расстояния СЕ и ЕF произвольной длины и втыкаем в точки Е и Fвехи. Став затем в точке F с булавочным прибором, намечаем направление FG, перпендикулярное к FC. Теперь, идя вдоль FG, отыскиваем на этой линии такую точку Н, из которой веха Е кажется покрывающей точку А. Это будет означать, что точки Н,Е и А лежат на одной прямой.
Задача решена: расстояние FH равно расстоянию АС, от которого достаточно лишь отнять ВС, чтобы получить искомую ширину реки.
Описанный выше способ можно видоизменить: отмерить на прямой CF не равные расстояния, а одно в несколько раз меньше другого. Например, отмерим FE в четыре раза меньше ЕС, а далее поступим попрежнему: по направлению FG, перпендикулярному к F, отыскиваем точку Н, из которой веха Е кажется покрывающей точку А. Но теперь уже ЕН не равно АС, а меньше этого расстояния в четыре раза: треугольники АСЕ и EFH здесь не равны, а подобны. Из подобия треугольников следует пропорция
АС:FH = СЕ:ЕF = 4:1. Значит, измерив расстояние FHи умножив результат на 4, получим расстояние АС, а отняв ВС, узнаем искомую ширину реки.

При помощи козырька
Способ этот состоит в следующем. Надо стать лицом к реке и надвинуть фуражку на глаз так, чтобы нижний обрез козырька точно совпал с линией противоположного берега. Козырек можно заменить ладонью руки или записной книжкой, плотно приложенной ребром ко лбу. Затем, не изменяя положения головы, надо повернуться направо или налево, или даже назад (в ту сторону, где поровней площадка, доступная для измерения расстояния) и заметить самую дальнюю точку, видимую из-под козырька (ладони, записной книжки).
Расстояние до этой точки и будет примерно равно ширине реки.

Глубина пруда.
Задача
Над озером тихим,
С полфута размером, высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой,
Нашел же рыбак его ранней весной
В двух путах от места, где рос.
Итак, предложу я вопрос: как озера вода
Здесь глубока?
(Перевод В.И.Лебедева)
Решение
Обозначим (рис.53) искомую глубину СD пруда через х. тогда, по теореме Пифагора, имеем:
ВD2 – х = ВС2,
т.е.
х2 = (х+1/2)2 – 22,
откуда
х2 = х + х + 1/4 – 4, х = 33/4.
Искомая глубина - 33/4 фута.
Близ берега реки или неглубокого пруда вы можете отыскать водяное растение, которое доставит вам реальный материал для подобной задачи: без всяких приспособлений, не замочив даже рук, определить глубину водоема в этом месте.

Скорость течения.
Меж селеньем и рощей нагорной
Вьется светлою лентой река
А.Фет.
На линиях, перпендикулярных к АВ, ставят еще две вехи С и D. Один из участников измерения с часами становится позади вехи D. Другой – с поплавком заходит несколько выше вехи А, поплавок бросает в воду, а сам становится позади вехи С. Оба смотрят вдоль направлений СА и DВ на поверхность воды. В тот момент, когда поплавок пересекает продолжение линии СА, первый наблюдатель взмахивает рукой. По этому сигналу второй наблюдатель засекает время первый раз и еще раз, когда поплавок пересечет направление DВ.
Предположим, что разность времени 20 секунд. Тогда скорость течения воды в реке:
= 0,5 м в секунду.

Пешеход на другом берегу.
Объясним, как ими воспользоваться. Пусть на рисунке 36 а и b - ваши глаза, точка М – конец пальца вытянутой руки, точка А – первое положение пешехода, В – второе. Треугольники аbМ и АВМ подобна ( вы должны повернуться к пешеходу так, чтобы аb было приблизительно параллельно направлению его движения). Значит, ВМ: bМ = АВ: аb – пропорция, в которой неизвестен только один член ВМ, все же остальные можно определить непосредственно. Действительно, bМ – длина вашей вытянутой руки; аb – расстояние между зрачками глаз, АВ измерено шагами пешехода (шаг можно принять в среднем равным ¾ м). следовательно, неизвестное расстояние от вас до пешехода на противоположном берегу реки
МВ = АВ * (bМ / аb).

Геометрия в открытом поле.
Посох Якова.
Он состоит из длинной линейки АВ в 70 – 100 см, по которой может скользить перпендикулярный к ней брусок СD и ОD скользящего бруска равны между собою. Если вы желаете при помощи этого бруска определить угловое расстояние между звездами S и S`, то приставляете к глазу конец А линейки (где для удобства наблюдения приделана просверленная пластинка) и направляете линейку так, чтобы звезда S` была видна у конца В линейки; затем двигаете поперечину СD вдоль линейки до тех пор, пока звезда S не будет видна как раз у конца С. Теперь остается лишь измерить расстояние АО, чтобы, зная длину СО, вычислить величину угла SАS`. Знакомые с тригонометрией сообразят, что тангенс искомого угла равен отношению СО/АО; вы вычисляете по теореме Пифагора длину АС, затем находите угол, синус которого равен СО/АС.
Наконец, вы можете узнать искомый угол и графическим путем: построив треугольник АСО на бумаге в произвольном масштабе, измеряете угол А транспортиром.
Для чего же нужна другая половина поперечины? На этот случай, когда измеряемый угол слишком велик, так что его не удается измерить сейчас указанным путем. Тогда на светило S` направляют на линейку АВ, а прямую АD, подвигая поперечину так, чтобы ее конец С пришелся в то же время у светила S. Найти величину угла SАS` вычислением или построением, конечно, не составит труда.

Искусство мерить шагами.
Отметим любопытное соотношение, обнаруженное многократными измерениями: средняя длина шага взрослого человека равна примерно половине его роста, считая до уровня глаз. Если, например, рост человека до глаз 1 м 40 см, то длина его шага – около 70 см. интересно при случае проверит это правило.