Сферическая поверхность. Шар 11 класс

Содержание
Сферическая поверхность
Уравнение сферы
Взаимное расположение сферы и плоскости
Касательная плоскость к сфере
Площадь сферы, объем шара
Вопросы

Сферическая поверхность
Сферической поверхностью называется геометрическое место точек пространства, равноудаленных от одной точки – центра.
Тело, ограниченное сферической поверхностью, называется шаром.

Сферическая поверхность
(продолжение)
O – центр сферы
R – радиус сферы
Ось – любая прямая, проходящая через центр сферы

Уравнение сферы
В прямоугольной системе координат уравнение сферы радиуса R
с центром C (xo;yo;zo) имеет вид:
(x-xo)²+(y-yo)²+(z-zo)²=R²

Взаимное расположение сферы и плоскости
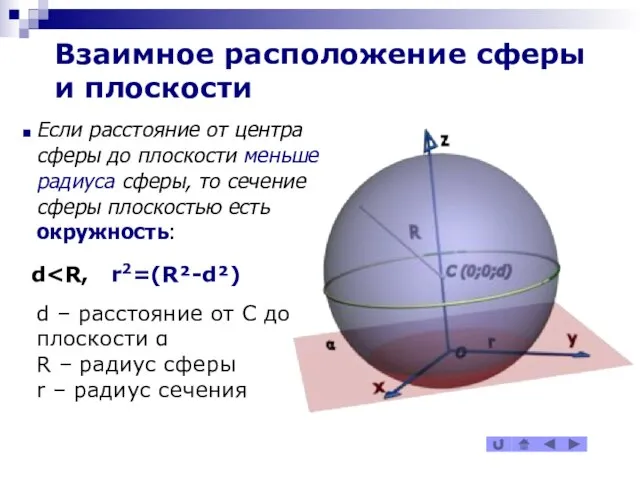
Если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность:
d

Взаимное расположение сферы и плоскости (продолжение)
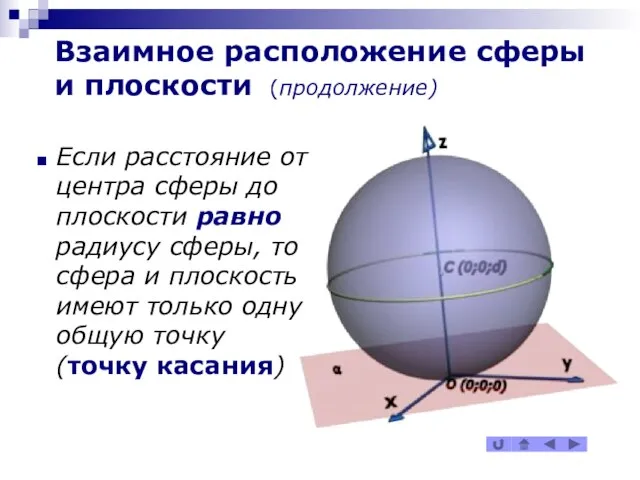
Если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку (точку касания)

Взаимное расположение сферы и плоскости (окончание)
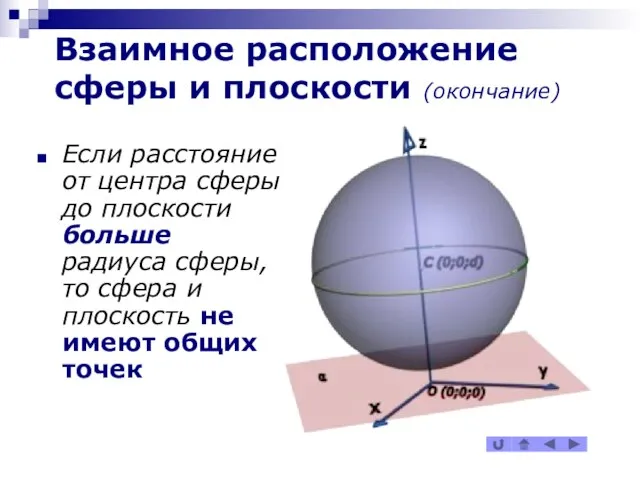
Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек

Касательная плоскость к сфере
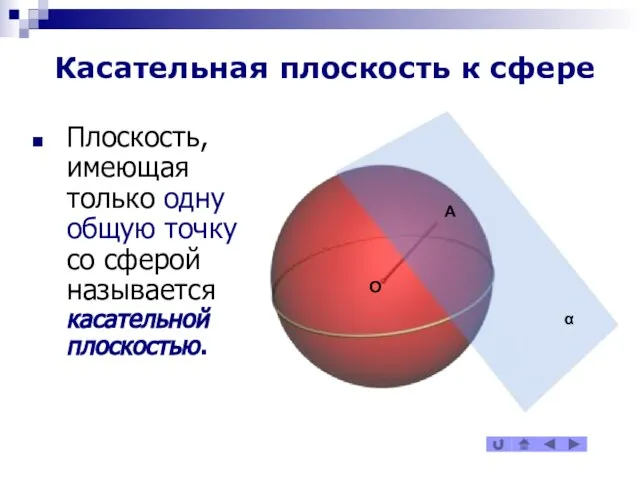
Плоскость, имеющая только одну общую точку со сферой называется касательной плоскостью.

Касательная плоскость к сфере (продолжение)
Теорема: Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Обратная теорема: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

Площадь сферы, объем шара
(продолжение)
Теорема Архимеда
Объем шара в полтора раза меньше объема описанного вокруг него цилиндра, а площадь поверхности шара в полтора раза меньше площади полной поверхности того же цилиндра:
V= (2/3)V1 S= (2/3)S1
где
V1 – объем описанного цилиндра,
S1 – площадь полной поверхности этого цилиндра

Площадь сферы, объем шара
Площадь поверхности шара радиуса R равна учетверенной площади большого круга:
S=4πR²
Объем шара радиуса R равен V = (4/3)πR³