Глава 2. Кратные криволинейные и поверхностные интегралы

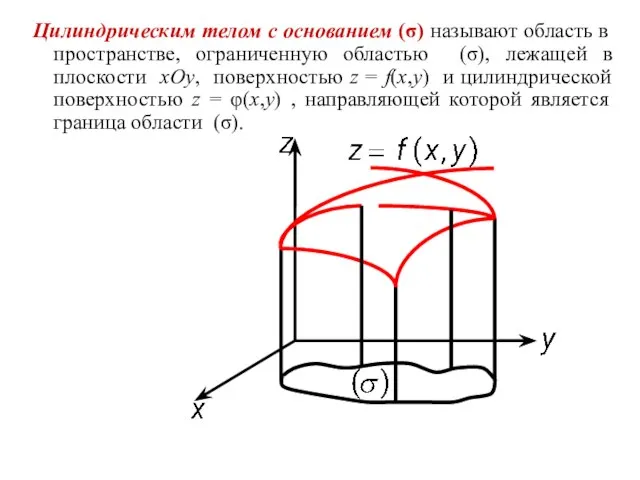
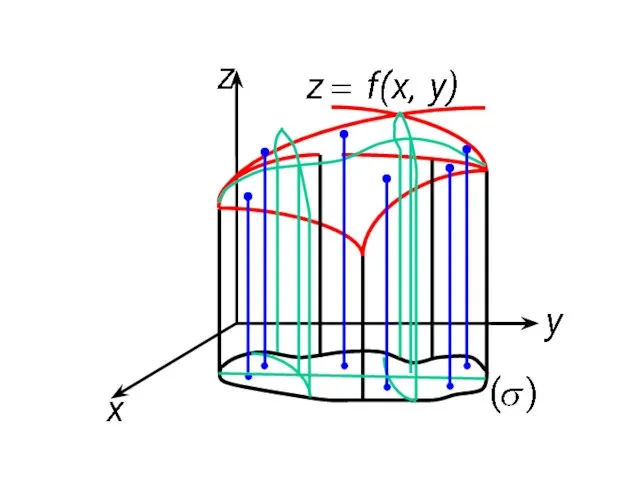
Цилиндрическим телом с основанием (σ) называют область в пространстве, ограниченную областью (σ), лежащей в плоскости xOy, поверхностью z = f(x,y) и цилиндрической поверхностью z = φ(x,y) , направляющей которой является граница области (σ).

2. Определение и свойства двойного интеграла
Пусть (σ) – квадрируемая (т.е. имеющая площадь) область в плоскости xOy, и в области (σ) задана функция z = f(x,y).
1. Разобьем область (σ) произвольным образом на n частей, не имеющих общих внутренних точек:
(Δσ1), (Δσ2), … , (Δσn).
2. В каждой области (Δσi) выберем произвольную точку Pi(ξi;ηi) и вычислим произведение f(Pi) · Δσi, где Δσi – площадь области (Δσi).
Сумму
назовем интегральной суммой для функции f(x,y) по области (σ) (соответствующей данному разбиению области (σ) и данному выбору точек Pi).

Диаметром множества G будем называть наибольшее расстояние между любыми двумя точками множества G .
Пусть di – диаметр (Δσi) ,

ТЕОРЕМА 1 (необходимое условие существования двойного интеграла). Если функция f(x,y) интегрируема в области (σ), то она ограничена в этой области.
ТЕОРЕМА 2 (достаточные условия существования двойного интеграла). Если
1) область (σ) – квадрируемая,
2) функция f(x,y) ограничена в области (σ) и непрерывна всюду за исключением некоторого множества точек площади нуль,
то f(x,y) интегрируема в области (σ) .

СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА
3. Постоянный множитель можно выносить за знак двойного интеграла, т.е.

4. Двойной интеграл от алгебраической суммы двух (конечного числа) функций равен алгебраической сумме двойных интегралов от этих функций, т.е.

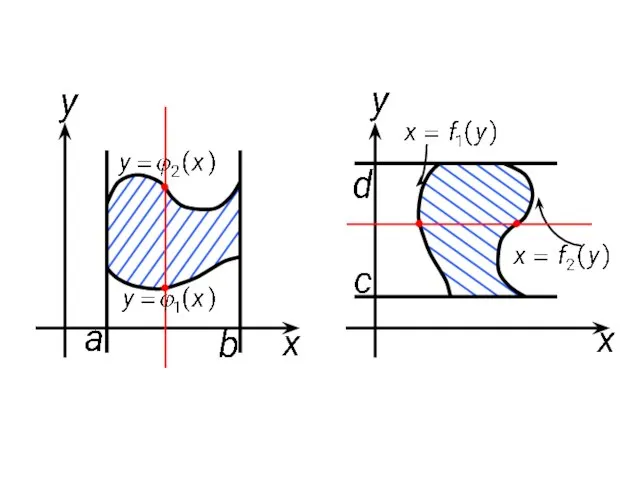
3. Вычисление двойного интеграла
Назовем область (σ) правильной в направлении оси Ox (Oy), если любая прямая, проходящая через внутреннюю точку области (σ) параллельно оси Ox (Oy) пересекает границу области в двух точках, причем, каждая из пересекаемых границ задается только одним уравнением.