Готовимся к ГИА

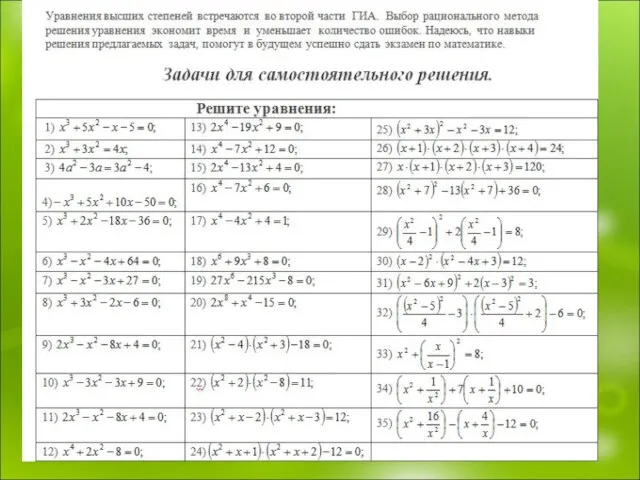
Уравнения, степень которых выше второй, решаются двумя основными методами: введением новой переменной и разложением на множители.
Метод введения новой переменной
Задание 1. Найти корни уравнения
Замечание: уравнения вида
где
Решение.
Данное уравнение можно свести к квадратному с помощью замены
получим
не удовлетворяет условию, т.к.
то
Ответ.
Не всегда замена переменных так очевидна, как при решении биквадратных уравнений.
называют биквадратными уравнениями.

Задание 2. Найти наименьший корень уравнения
Решение.
Рассмотрим первое слагаемое
Зная, что
.
Сгруппируем второе и третье слагаемое
Вынесем общий множитель 3 за скобки, тогда имеем
Введем новую переменную
тогда исходное уравнение будет иметь вид
, получили квадратное уравнение относительно переменной
. Решим его.
,
не удовлетворяет условию, т.к.
то вернемся к переменной
то
или
или
Прежде чем записать ответ, вспомним, на какой вопрос требуется ответить в задании.
- 5 – наименьший корень уравнения.
Ответ. -5.

Задание 3. Решите уравнение
Решение.
Вначале сгруппируем множители следующим образом:
раскрыв внутренние скобки, получим уравнение
Введем новую переменную
тогда исходное уравнение будет иметь вид
получили квадратное уравнение относительно переменной
. Решим его.
то вернемся к переменной
Если
то
Если
то
уравнение не имеет действительных корней.
Ответ. -2,5;2.

Задание 4. Решите уравнение
Решение.
Введем новую переменную
тогда исходное уравнение будет иметь
вид
не удовлетворяет условию, т.к.
Если
то
или
или
Ответ.

Задание 5. Решите уравнение
Введем новую переменную
Решение.
получили
Если
Если
Ответ.-5;1;

Задание 6. Решите уравнение
Решение.
В левой части уравнения выделим полный квадрат
Введем новую переменную
получили квадратное уравнение относительно переменной
. Решим его.
Если
то
уравнение не имеет действительных корней.
Если
то
Ответ. 2,-1

Возвратные уравнения
Уравнение вида
на симметричных позициях, равны, то есть если
при
Рассмотрим возвратное уравнение четвертой степени вида
где
некоторые числа, причём
Уравнение удобно решать с помощью следующего алгоритма:
- разделить левую и правую части уравнения на
При этом не происходит потери решения, так как
не является корнем исходного уравнения при
- группировкой привести уравнение к виду
- ввести новую переменную
тогда
то есть
в новых переменных рассматриваемое уравнение является квадратным
- решить его относительно
возвратиться к исходной переменной.
называется возвратным, если его коэффициенты, стоящие

Задание 7. Решите уравнение
Решение.
Разделим обе части уравнения на получим
После группировки получаем
Введём новую переменную тогда
то есть то
получили квадратное уравнение относительно переменной t
Решим его.
Если то
Если то, уравнение не имеет действительных корней.
Ответ.
Для возвратных уравнений более высоких степеней верны следующие утверждения
Возвратные уравнения чётной степени сводится к уравнению вдвое меньшей степени
подстановкой
Возвратные уравнения нечётной степени обязательно имеет корень и после деления многочлена, стоящего в левой части этого уравнения, на двучлен приводится к возвратному уравнению чётной степени.

Метод разложения на множители
Задание 8. Сколько корней имеет уравнение (ГИА-2010)
Решение.
В левой части уравнения четыре слагаемых, поэтому применим метод группировки, разложим на множители левую часть уравнения. Получим:
данное уравнение равносильно совокупности
1.
2.
Уравнение имеет три корня: 3; .
Ответ. 3.

Задание 9. Решите уравнение
Решение.
Решим данное уравнение способом разложения левой части на множители.
Получим
разложим левую часть уравнения на множители, используя формулу суммы кубов
данное уравнение равносильно совокупности
1.
2. уравнение не имеет действительных корней.
Ответ.

Задание 10. Решите уравнение
Решение.
Решим данное уравнение способом разложения левой части на множители. Получим
разложим левую часть уравнения на множители, используя формулу разности квадратов
данное уравнение равносильно совокупности
1.
2.
уравнение не имеет действительных корней.
Ответ.