Содержание
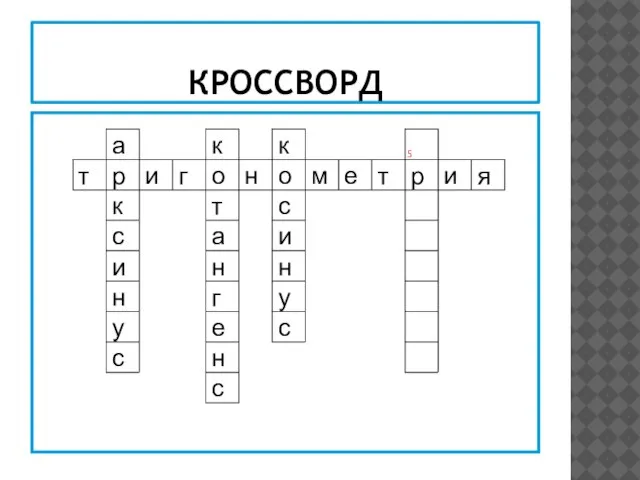
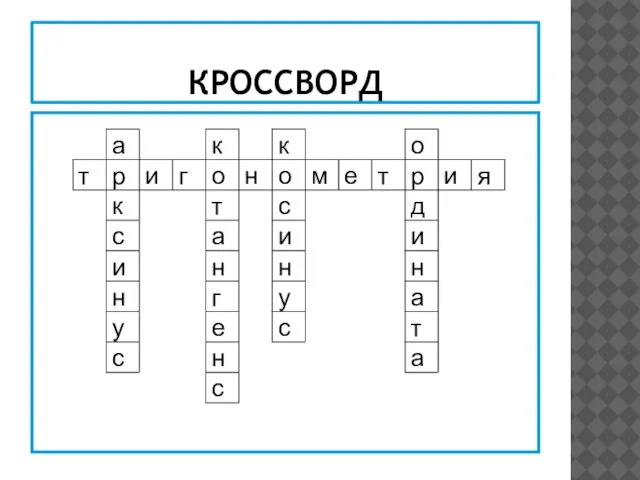
- 2. КРОССВОРД
- 3. КРОССВОРД
- 4. КРОССВОРД
- 5. КРОССВОРД
- 6. КРОССВОРД
- 7. КРОССВОРД
- 8. ЧТОБЫ ПРАВИЛЬНО РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ НАДО: 1) уметь отмечать точки на числовой окружности; 2) уметь определять
- 9. ВЫЧИСЛИ УСТНО:
- 10. ОТВЕТЫ:
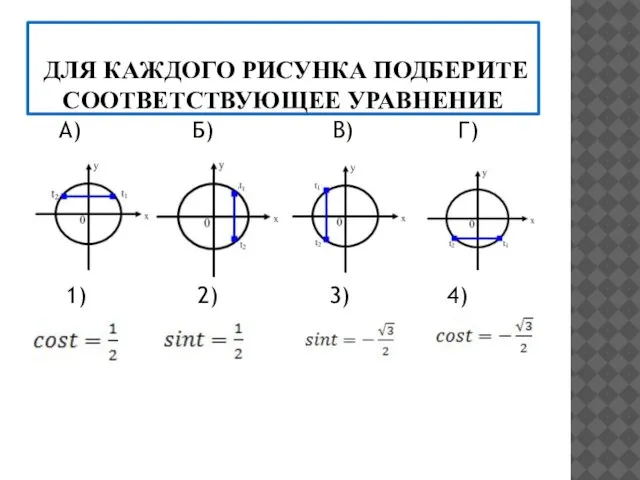
- 11. ДЛЯ КАЖДОГО РИСУНКА ПОДБЕРИТЕ СООТВЕТСТВУЮЩЕЕ УРАВНЕНИЕ А) Б) В) Г) 1) 2) 3) 4)
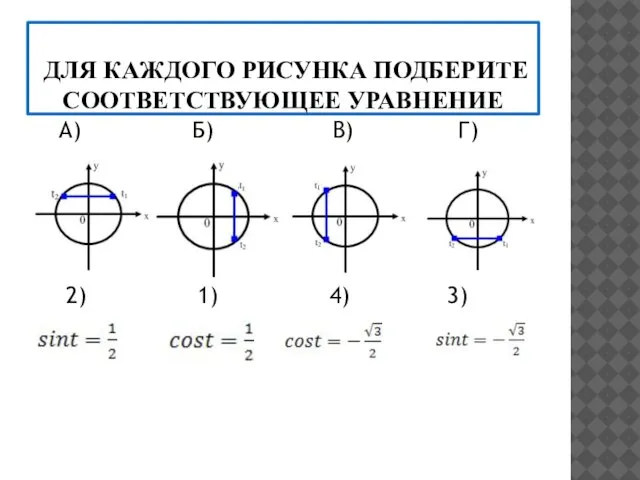
- 12. ДЛЯ КАЖДОГО РИСУНКА ПОДБЕРИТЕ СООТВЕТСТВУЮЩЕЕ УРАВНЕНИЕ А) Б) В) Г) 2) 1) 4) 3)
- 13. УСТАНОВИТЕ СООТВЕТСТВИЕ: 1) sin x = 0 а) 2) cos x = -1 б) 3) sin
- 14. УСТАНОВИТЕ СООТВЕТСТВИЕ: 1) sin x = 0 а) 2) cos x = -1 б) 3) sin
- 15. УСТАНОВИТЕ СООТВЕТСТВИЕ: 1) sin x = 0 а) 2) cos x = -1 б) 3) sin
- 16. УСТАНОВИТЕ СООТВЕТСТВИЕ: 1) sin x = 0 а) 2) cos x = -1 б) 3) sin
- 17. УСТАНОВИТЕ СООТВЕТСТВИЕ: 1) sin x = 0 а) 2) cos x = -1 б) 3) sin
- 18. УСТАНОВИТЕ СООТВЕТСТВИЕ: 1) sin x = 0 а) 2) cos x = -1 б) 3) sin
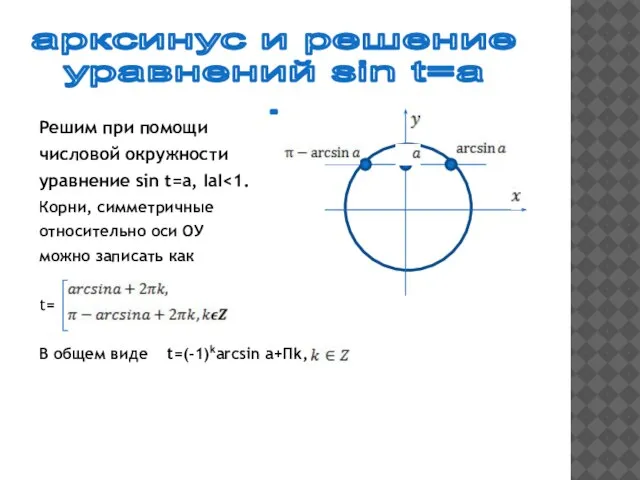
- 19. Решим при помощи числовой окружности уравнение sin t=a, IаI Корни, симметричные относительно оси ОУ можно записать
- 20. sin t = а ,|a| Частные случаи: а = 0 а = -1 а = 1
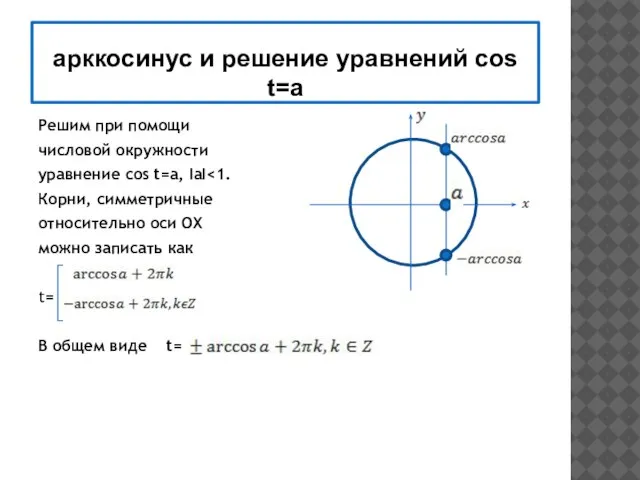
- 21. арккосинус и решение уравнений соs t=a Решим при помощи числовой окружности уравнение cos t=a, IаI Корни,
- 22. соs t =а , |a| Частные случаи: а = 0 а = -1 а = 1
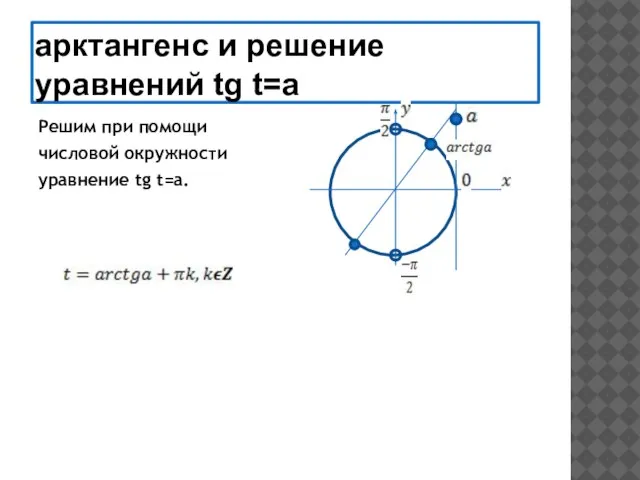
- 23. арктангенс и решение уравнений tg t=a Решим при помощи числовой окружности уравнение tg t=a.
- 24. tg t = а Частные случаи: а = 0 а = -1 а = 1 t
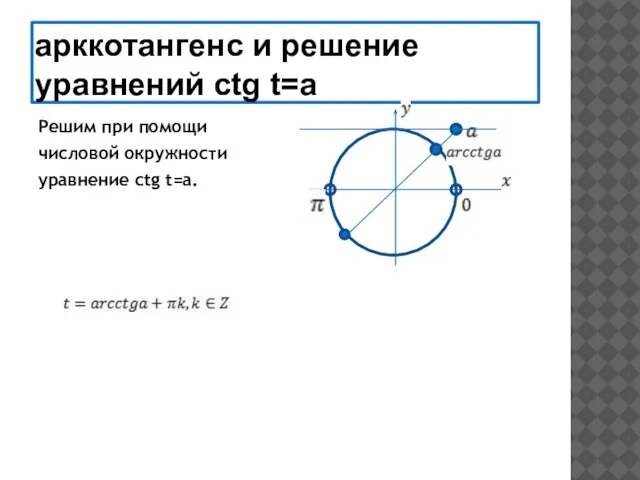
- 25. арккотангенс и решение уравнений ctg t=a Решим при помощи числовой окружности уравнение ctg t=a.
- 26. сtg t = а, Частные случаи: а = 0 а = -1 а = 1 t
- 27. ЗАПОМНИ а=0 а=1 а=-1 |a|
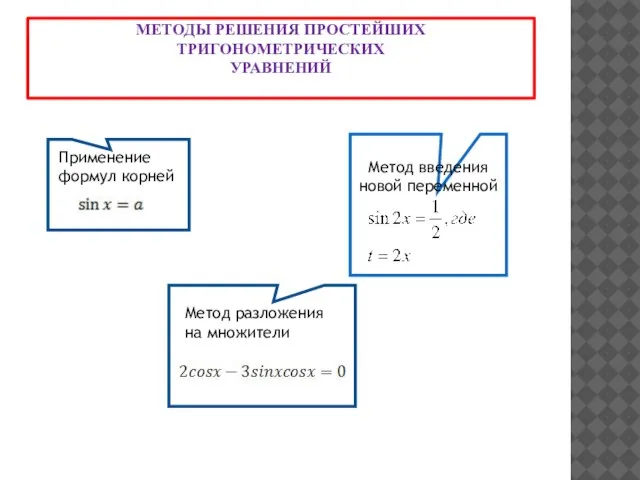
- 28. МЕТОДЫ РЕШЕНИЯ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ghb Применение формул корней Метод введения новой переменной V Метод разложения
- 29. НАША ЗАДАЧА: СВЕСТИ ЛЮБОЕ ТРИГОНОМЕТРИЧЕСКОЕ УРАВНЕНИЕ К ПРОСТЕЙШЕМУ ВИДУ.
- 30. ПРИМЕРЫ УРАВНЕНИЙ х= ±arccos а + 2 k, k є Z
- 31. ПРИМЕРЫ УРАВНЕНИЙ х = (-1)n arcsin a+πn,n є z 2х = (-1)n 2х = (-1)n х
- 32. ПРИМЕРЫ УРАВНЕНИЙ Это частный вид уравнения cos t=0, t=
- 33. ПРИМЕРЫ УРАВНЕНИЙ x = arctg a + πk,k є z
- 34. РЕШИ САМ Уровень А Уровень Б Решите уравнения: 1. 1. 2. 2. 3. 3.
- 35. РЕШИ САМ Уровень А Уровень Б УРА САМ МОЛОДЦЫ
- 37. Скачать презентацию





















 Практикалық психологтың міндеттері, құқықтары, этикалық кодесі
Практикалық психологтың міндеттері, құқықтары, этикалық кодесі Ковров фильм представляет. С днем рождения. Фотоальбом
Ковров фильм представляет. С днем рождения. Фотоальбом Партии прошедшие порог в государственную думу
Партии прошедшие порог в государственную думу Протяжные станки. Современные технологии в мире протягивания
Протяжные станки. Современные технологии в мире протягивания Вирусные гепатиты ВИЧ-инфекция
Вирусные гепатиты ВИЧ-инфекция  Презентация на тему Иван Андреевич Крылов Басни Квартет Волк на Псарне
Презентация на тему Иван Андреевич Крылов Басни Квартет Волк на Псарне Ручные работы
Ручные работы Принцип относительности Галилея
Принцип относительности Галилея Установление руководящего контроля методами прикладного анализа поведения
Установление руководящего контроля методами прикладного анализа поведения Эндокринная Артериальная гипертензия
Эндокринная Артериальная гипертензия Lecture 5
Lecture 5 Разнообразие растений на Земле
Разнообразие растений на Земле Оползни, сели, обвалы, лавины
Оползни, сели, обвалы, лавины Презентация на тему Многоугольники (1 класс)
Презентация на тему Многоугольники (1 класс) Экологические проблемы Байкала
Экологические проблемы Байкала 1426585
1426585 Презентация на тему Международная классификация внешнеторговых документов по группам
Презентация на тему Международная классификация внешнеторговых документов по группам  Оценка деятельности PR-департамента в Тройке Диалог Декабрь 2011 | Тройка Диалог. - презентация
Оценка деятельности PR-департамента в Тройке Диалог Декабрь 2011 | Тройка Диалог. - презентация Предмет, цель и задачи эстетики
Предмет, цель и задачи эстетики 20140123_raspredelenie_solnechnogo_tepla_i_sveta
20140123_raspredelenie_solnechnogo_tepla_i_sveta Использование языка Data Analysis Expressions в PowerPivot
Использование языка Data Analysis Expressions в PowerPivot Финансовое обеспечение выполнения государственного заданияР.С. Афанасьевк.э.н., ведущий консультант«ООО ЭКОРИС-НЭИ»
Финансовое обеспечение выполнения государственного заданияР.С. Афанасьевк.э.н., ведущий консультант«ООО ЭКОРИС-НЭИ» Адаптация первоклассников к школьному обучению
Адаптация первоклассников к школьному обучению Понимание красоты человека в европейском и русском искусстве
Понимание красоты человека в европейском и русском искусстве Классификация прокатных станов
Классификация прокатных станов Презентация по теме: «Сечения, разрезы, их виды и применение»
Презентация по теме: «Сечения, разрезы, их виды и применение» Радиационная защита. Дозиметрия
Радиационная защита. Дозиметрия Приемлемость рисков в трудовом процессе. Программа Near Miss
Приемлемость рисков в трудовом процессе. Программа Near Miss