Графа и его элементы

ГРАФОМ G = (V, X) НАЗЫВАЕТСЯ ПАРА ДВУХ КОНЕЧНЫХ МНОЖЕСТВ: МНОЖЕСТВО ТОЧЕК И МНОЖЕСТВО ЛИНИЙ, СОЕДИНЯЮЩИХ НЕКОТОРЫЕ ПАРЫ ТОЧЕК.
ВПЕРВЫЕ ПОНЯТИЕ «ГРАФ» ВВЕЛ В 1936 г. ВЕНГЕРСКИЙ МАТЕМАТИК ДЕННИ КЁНИГ. НО ПЕРВАЯ РАБОТА ПО ТЕОРИИ ГРАФОВ ПРИНАДЛЕЖАЛА ПЕРУ ВЕЛИКОГО ЛЕОНАРДА ЭЙЛЕРА И БЫЛА НАПИСАНА ЕЩЕ В 1736 г.

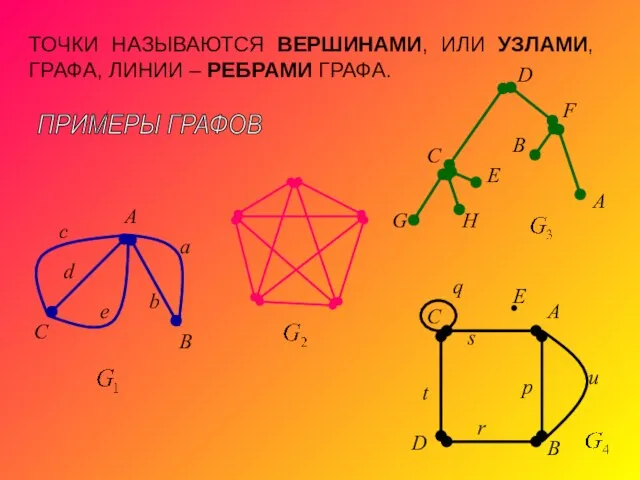
ТОЧКИ НАЗЫВАЮТСЯ ВЕРШИНАМИ, ИЛИ УЗЛАМИ, ГРАФА, ЛИНИИ – РЕБРАМИ ГРАФА.
ПРИМЕРЫ ГРАФОВ

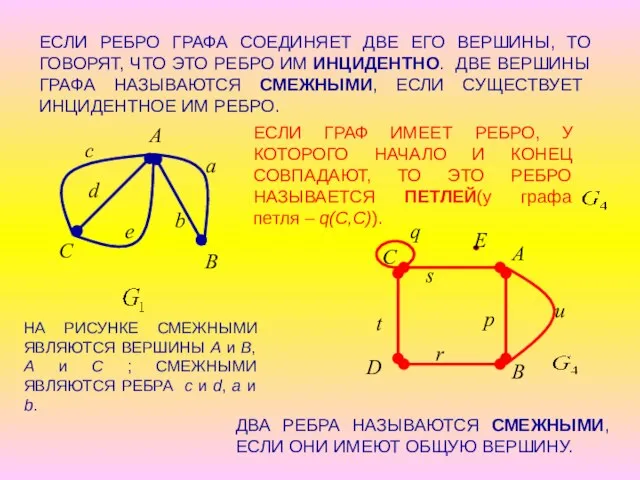
ЕСЛИ РЕБРО ГРАФА СОЕДИНЯЕТ ДВЕ ЕГО ВЕРШИНЫ, ТО ГОВОРЯТ, ЧТО ЭТО РЕБРО ИМ ИНЦИДЕНТНО. ДВЕ ВЕРШИНЫ ГРАФА НАЗЫВАЮТСЯ СМЕЖНЫМИ, ЕСЛИ СУЩЕСТВУЕТ ИНЦИДЕНТНОЕ ИМ РЕБРО.
НА РИСУНКЕ СМЕЖНЫМИ ЯВЛЯЮТСЯ ВЕРШИНЫ A и B, A и C ; СМЕЖНЫМИ ЯВЛЯЮТСЯ РЕБРА c и d, a и b.
ЕСЛИ ГРАФ ИМЕЕТ РЕБРО, У КОТОРОГО НАЧАЛО И КОНЕЦ СОВПАДАЮТ, ТО ЭТО РЕБРО НАЗЫВАЕТСЯ ПЕТЛЕЙ(у графа петля – q(C,C)).
A
B
C
D
E
u
p
s
t
r
q
ДВА РЕБРА НАЗЫВАЮТСЯ СМЕЖНЫМИ, ЕСЛИ ОНИ ИМЕЮТ ОБЩУЮ ВЕРШИНУ.

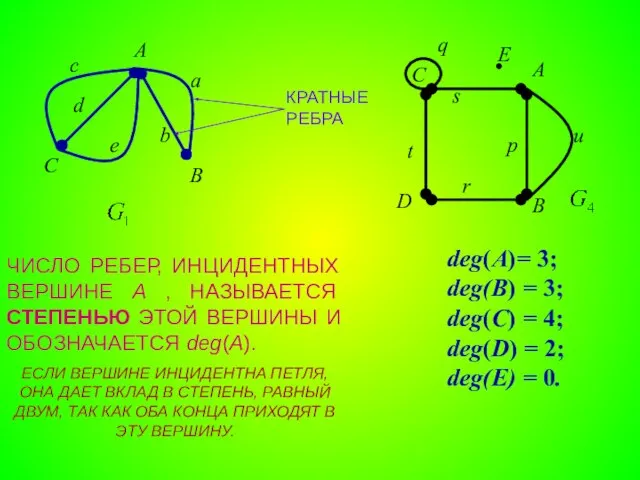
КРАТНЫЕ РЕБРА
ЧИСЛО РЕБЕР, ИНЦИДЕНТНЫХ ВЕРШИНЕ A , НАЗЫВАЕТСЯ СТЕПЕНЬЮ ЭТОЙ ВЕРШИНЫ И ОБОЗНАЧАЕТСЯ deg(A).
ЕСЛИ ВЕРШИНЕ ИНЦИДЕНТНА ПЕТЛЯ, ОНА ДАЕТ ВКЛАД В СТЕПЕНЬ, РАВНЫЙ ДВУМ, ТАК КАК ОБА КОНЦА ПРИХОДЯТ В ЭТУ ВЕРШИНУ.
deg(A)= 3; deg(B) = 3; deg(C) = 4; deg(D) = 2; deg(E) = 0.

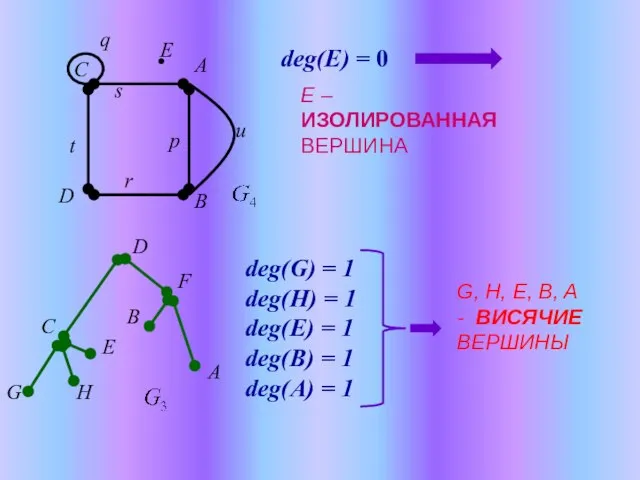
deg(E) = 0
E – ИЗОЛИРОВАННАЯ ВЕРШИНА
deg(G) = 1
deg(H) = 1
deg(E) = 1
deg(B) = 1
deg(A) = 1
G, H, E, B, A - ВИСЯЧИЕ ВЕРШИНЫ

ТЕОРЕМА
В ГРАФЕ G(V, X) СУММА СТЕПЕНЕЙ ВСЕХ ЕГО ВЕРШИН – ЧИСЛО ЧЕТНОЕ, РАВНОЕ УДВОЕННОМУ ЧИСЛУ РЕБЕР ГРАФА:
ВЕРШИНА НАЗЫВАЕТСЯ ЧЕТНОЙ (НЕЧЕТНОЙ), ЕСЛИ ЕЕ СТЕПЕНЬ – ЧЕТНОЕ(НЕЧЕТНОЕ) ЧИСЛО.
ТЕОРЕМА
ЧИСЛО НЕЧЕТНЫХ ВЕРШИН ЛЮБОГО ГРАФА – ЧЕТНО.
СЛЕДСТВИЕ
НЕВОЗМОЖНО НАЧЕРТИТЬ ГРАФ С НЕЧЕТНЫМ ЧИСЛОМ НЕЧЕТНЫХ ВЕРШИН.

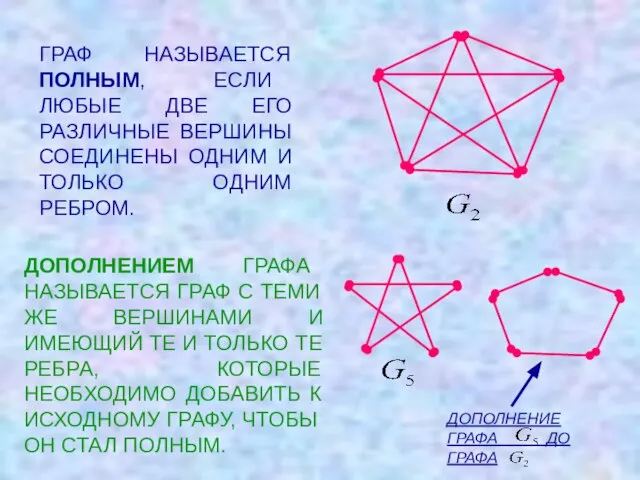
ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО РАЗЛИЧНЫЕ ВЕРШИНЫ СОЕДИНЕНЫ ОДНИМ И ТОЛЬКО ОДНИМ РЕБРОМ.
ДОПОЛНЕНИЕМ ГРАФА НАЗЫВАЕТСЯ ГРАФ С ТЕМИ ЖЕ ВЕРШИНАМИ И ИМЕЮЩИЙ ТЕ И ТОЛЬКО ТЕ РЕБРА, КОТОРЫЕ НЕОБХОДИМО ДОБАВИТЬ К ИСХОДНОМУ ГРАФУ, ЧТОБЫ ОН СТАЛ ПОЛНЫМ.
ДОПОЛНЕНИЕ ГРАФА ДО ГРАФА

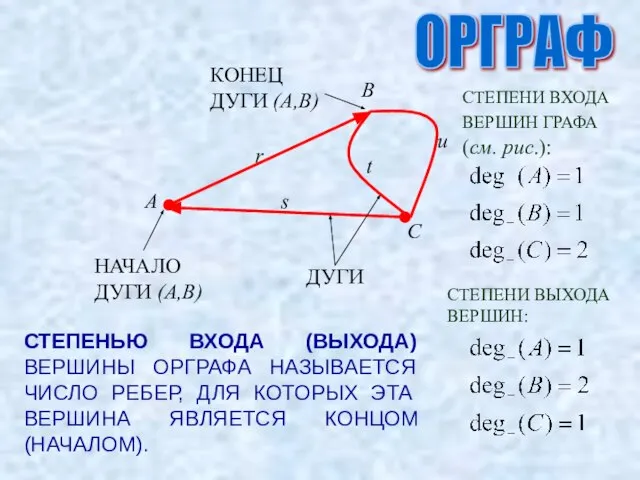
ОРГРАФ
ДУГИ
НАЧАЛО ДУГИ (A,B)
КОНЕЦ ДУГИ (A,B)
СТЕПЕНЬЮ ВХОДА (ВЫХОДА) ВЕРШИНЫ ОРГРАФА НАЗЫВАЕТСЯ ЧИСЛО РЕБЕР, ДЛЯ КОТОРЫХ ЭТА ВЕРШИНА ЯВЛЯЕТСЯ КОНЦОМ (НАЧАЛОМ).
СТЕПЕНИ ВХОДА ВЕРШИН ГРАФА (см. рис.):
СТЕПЕНИ ВЫХОДА ВЕРШИН:

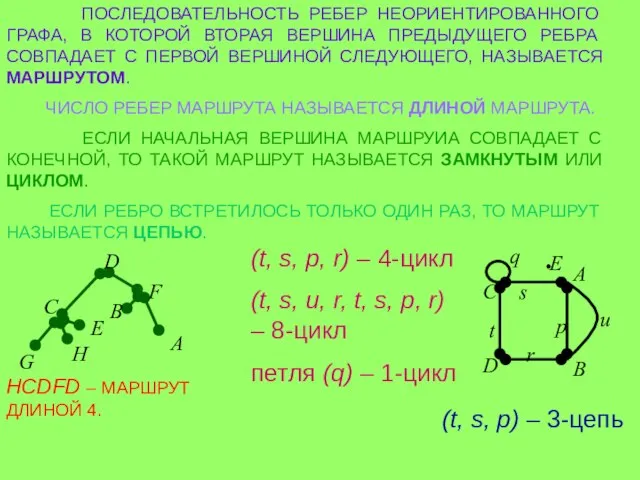
ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР НЕОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ ВТОРАЯ ВЕРШИНА ПРЕДЫДУЩЕГО РЕБРА СОВПАДАЕТ С ПЕРВОЙ ВЕРШИНОЙ СЛЕДУЮЩЕГО, НАЗЫВАЕТСЯ МАРШРУТОМ.
ЧИСЛО РЕБЕР МАРШРУТА НАЗЫВАЕТСЯ ДЛИНОЙ МАРШРУТА.
ЕСЛИ НАЧАЛЬНАЯ ВЕРШИНА МАРШРУИА СОВПАДАЕТ С КОНЕЧНОЙ, ТО ТАКОЙ МАРШРУТ НАЗЫВАЕТСЯ ЗАМКНУТЫМ ИЛИ ЦИКЛОМ.
ЕСЛИ РЕБРО ВСТРЕТИЛОСЬ ТОЛЬКО ОДИН РАЗ, ТО МАРШРУТ НАЗЫВАЕТСЯ ЦЕПЬЮ.
G
H
E
C
D
F
A
B
HCDFD – МАРШРУТ ДЛИНОЙ 4.
A
B
C
D
E
u
p
s
t
r
q
(t, s, p, r) – 4-цикл
(t, s, u, r, t, s, p, r) – 8-цикл
петля (q) – 1-цикл
(t, s, p) – 3-цепь

ПУТЬ – УПОРЯДОЧЕННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР ОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ КОНЕЦ ПРЕДЫДУЩЕГО РЕБРА СОВПАДАЕТ С НАЧАЛОМ СЛЕДУЮЩЕГО И ВСЕ РЕБРА ЕДИНСТВЕННЫ.
ЦИКЛ В ОРГРАФЕ – ПУТЬ, У КОТОРОГО СОВПАДАЮТ НАЧАЛО И КОНЕЦ.
(u, s, r, t) – 4-путь
(r, u) – 2-путь
(s, r, t) и (u, s, r) – 3-циклы

ЦЕПЬ, ПУТЬ И ЦИКЛ В ГРАФЕ НАЗЫВАЮТСЯ ПРОСТЫМИ, ЕСЛИ ОНИ ПРОХОДЯТ ЧЕРЕЗ ЛЮБУЮ ИЗ ВЕРШИН НЕ БОЛЕЕ ОДНОГО РАЗА.
НЕОРИЕНТИРОВАННЫЙ ГРАФ НАЗЫВАЕТСЯ СВЯЗНЫМ, ЕСЛИ МЕЖДУ ЛЮБЫМИ ДВУМЯ ЕГО ВЕРШИНАМИ ЕСТЬ МАРШРУТ.
ТЕОРЕМА
ДЛЯ ТОГО, ЧТОБЫ СВЯЗНЫЙ ГРАФ ЯВЛЯЛСЯ ПРОСТЫМ ЦИКЛОМ, НЕОБХОДИМО И ДОСТАТОЧНО, ЧТОБЫ КАЖДАЯ ЕГО ВЕРШИНА ИМЕЛА СТЕПЕНЬ, РАВНУЮ 2.

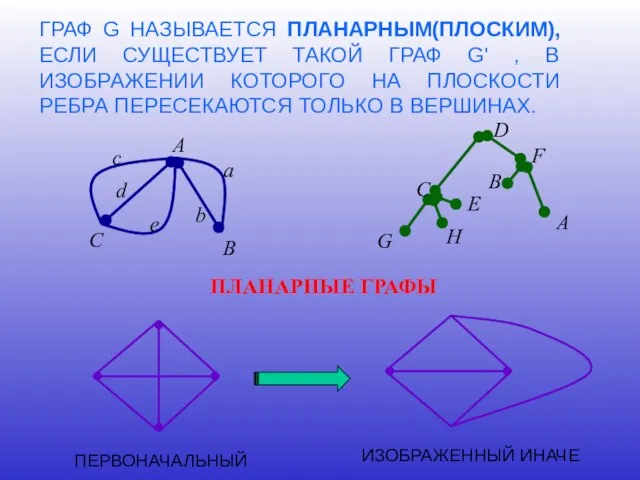
ГРАФ G НАЗЫВАЕТСЯ ПЛАНАРНЫМ(ПЛОСКИМ), ЕСЛИ СУЩЕСТВУЕТ ТАКОЙ ГРАФ G' , В ИЗОБРАЖЕНИИ КОТОРОГО НА ПЛОСКОСТИ РЕБРА ПЕРЕСЕКАЮТСЯ ТОЛЬКО В ВЕРШИНАХ.
C
A
B
a
b
c
d
e
G
H
E
C
D
F
A
B
ПЛАНАРНЫЕ ГРАФЫ
ПЕРВОНАЧАЛЬНЫЙ
ИЗОБРАЖЕННЫЙ ИНАЧЕ

ЭЙЛЕРОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), КОТОРЫЙ СОДЕРЖИТ ВСЕ РЕБРА ГРАФА ТОЛЬКО ОДИН РАЗ.
ГРАФ, ОБЛАДАЮЩИЙ ЭЙЛЕРОВЫМ ЦИКЛОМ, НАЗЫВАЕТСЯ ЭЙЛЕРОВЫМ.
ТЕОРЕМА
ГРАФ ЯВЛЯЕТСЯ ЭЙЛЕРОВЫМ ТОГДА И ТОЛЬКО ТОГДА, КОГДА ОН – СВЯЗНЫЙ ГРАФ, ИМЕЮЩИЙ ВСЕ ЧЕТНЫЕ ВЕРШИНЫ.

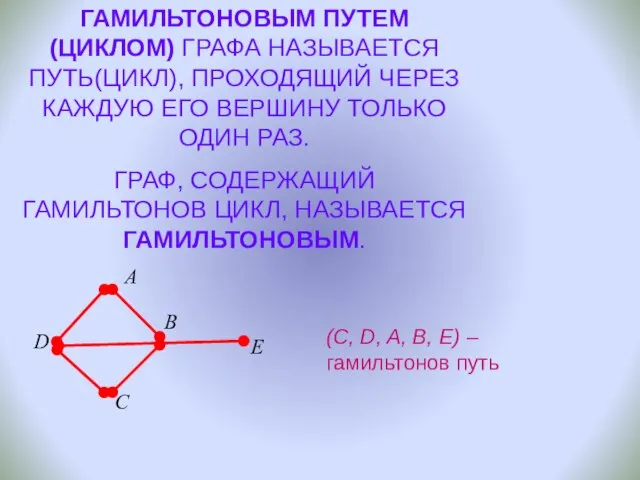
ГАМИЛЬТОНОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ КАЖДУЮ ЕГО ВЕРШИНУ ТОЛЬКО ОДИН РАЗ.
ГРАФ, СОДЕРЖАЩИЙ ГАМИЛЬТОНОВ ЦИКЛ, НАЗЫВАЕТСЯ ГАМИЛЬТОНОВЫМ.
A
B
C
D
E
(C, D, A, B, E) – гамильтонов путь

МАТРИЦЕЙ ИНЦИДЕНТНОСТИ ГРАФА G НАЗЫВАЮТ ТАБЛИЦУ B, СОСТОЯЩУЮ ИЗ n СТРОК(ВЕРШИНЫ) И m СТОЛБЦОВ(РЕБРА), В КОТОРОЙ:
ДЛЯ НЕОРИЕНТИРОВАННОГО ГРАФА:
, ЕСЛИ ВЕРШИНА
ИНЦИДЕНТНА РЕБРУ
, ЕСЛИ ВЕРШИНА
ИНЦИДЕНТНА РЕБРУ
ДЛЯ ОРИЕНТИРОВАННОГО ГРАФА:
, ЕСЛИ ВЕРШИНА
ЯВЛЯЕТСЯ НАЧАЛОМ ДУГИ
, ЕСЛИ ВЕРШИНА
НЕ ИНЦИДЕНТНА ДУГЕ
, ЕСЛИ ВЕРШИНА
ЯВЛЯЕТСЯ КОНЦОМ ДУГИ

МАТРИЦЕЙ СМЕЖНОСТИ ГРАФА G(V,X) БЕЗ КРАТНЫХ РЕБЕР НАЗЫВАЮТ КВАДРАТНУЮ МАТРИЦУ A ПОРЯДКА n, В КОТОРОЙ:
, ЕСЛИ
, ЕСЛИ

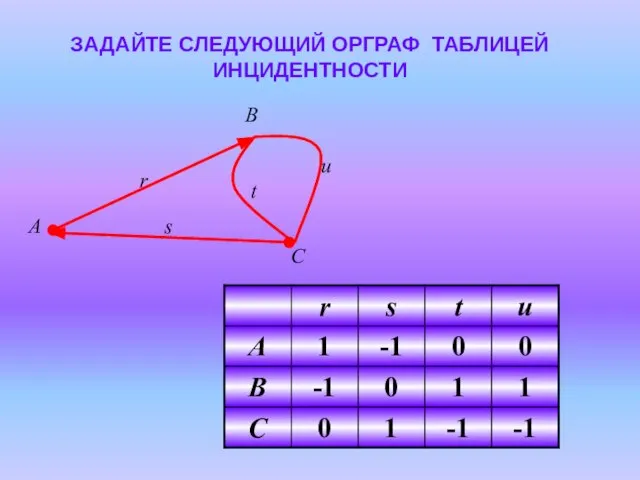
ЗАДАЙТЕ СЛЕДУЮЩИЙ ОРГРАФ ТАБЛИЦЕЙ ИНЦИДЕНТНОСТИ

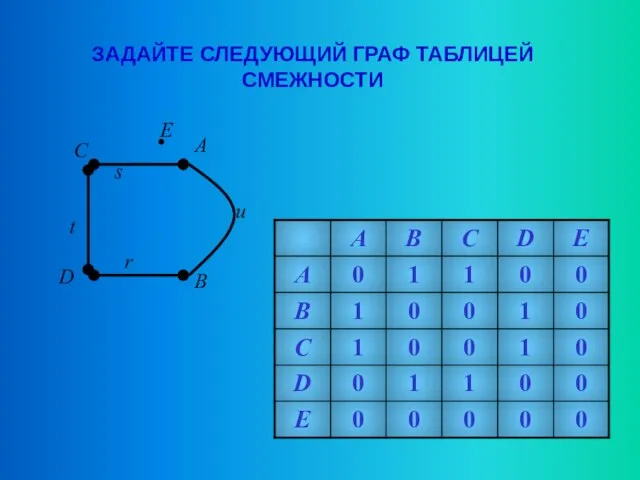
ЗАДАЙТЕ СЛЕДУЮЩИЙ ГРАФ ТАБЛИЦЕЙ СМЕЖНОСТИ
A
B
C
D
E
u
s
t
r