информатика 10 класс система счисления

Я бы хотела, чтобы моя презентация помогла ученикам 10-х классов повторить материал, изученный за учебный год. Посмотрев мою презентацию, они смогут освежить свои знания, поработать над темами, которые были им не очень понятны в процессе учебы и в конце подготовки проверить свои знания.
Презентация содержит теоретический материал для подготовки и тесты для проверки полученных знаний.
Цели:

Теоритический материал
Тест

МЕНЮ
Темы
Количество возможных событий и количество информации
Единицы измерения количества информации
Формула Шеннона
Системы счисления
Арифметические операции в разных системах счисления
Представление чисел в компьютере
Формы мышлния. Алгебра высказываний
Логические законы и правила преобразования логических выражений
Совершенная дизъюнктивная нормальная форма
Совершенная конъюнктивная нормальная форма

За единицу количества информации принимается такое количество информации, которое содержит сообщение, уменьшающее неопределенность в два раза. Такая единица названа «бит».
1 байт = 23 байт = 8 бит
1 Кбайт = 210 байт = 1024 байт
1 Мбайт = 210 Кбайт = 1024 Кбайт
1 Гбайт = 210 Мбайт = 1024 Мбайт
Единицы измерения количества информации

Существует формула, которая связывает между собой количество возможных событий N и количество информации I.
N = 2I
По этой формуле можно легко определить количество возможных событий, если известно количество информации
N = 24 = 16
или количество информации, если известно количество возможных событий
32 = 2I
I = 5
Количество возможных событий и количество информации

При равновероятных событиях используется формула N = 2I
При неравновероятных событиях используется формула Шеннона
1) I = Log2 1 / p
2) P= K / N
P – мощность алфавита
K – количество определенного события
N – количество всего события
Формула Шеннона
пример задачи
для равновероятного
события
пример задачи
для неравновероятного
события

пример задачи
для равновероятного
события
Какой объем имеет 2-х сторонняя дискета, если каждая сторона имеет 40 дорожек по 15 секторов на каждой, каждый сектор содержит 512 символов, 64-х символьного алфавита?
64 = 2I 64 = 26 I = 6 бит – один символ
512 * 6 = 3072 бит
3072 * 15 = 46080 бит – одна дорожка
40 * 46080 = 1843200 бит
1843200 : 8 = 230400 байт
230400 : 1024 = 225 Кбайт
225 * 2 = 450 Кбайт
Ответ: 450 Кбайт

пример задачи
для неравновероятного
события
В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш несет 4 бита информации. Сколько белых карандашей было в коробке?
I (бел) = Log2 1 / P(бел) 4 = Log2 1 / X
24 = 1 / P(бел) P(бел) = 1 / 16
16 = 1 / P(бел) P(бел) = K(бел) / N
K(бел) = P(бел) * N
K(бел) = 1/ 16 * 64 = 4
Ответ: 4 штуки

Системы счисления
Двоичная (2) – 0 , 1
Восьмеричная (8) – 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7
Десятичная (10) – 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9
Шестнадцатеричная (16) – 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , А(10), В(11), С(12), D(13), E (14), F (15)
Не существует прямого перевода из восьмеричной системы счисления в шестнадцатеричную и наоборот.
10
2

Десятичная
Чтобы число из десятичной системы перевести в любую другую, надо делить на ту систему, в которую переводим, нацело и записать с конца.
25 10 2, 8, 16
2 25 8 25 16
12 2 24 3 16 1
1 12 6 2 1 9
0 6 3 2
0 2 1
1
110012 138 1916

Десятичная
Для перевода числа в десятичную систему из любой другой, нужно записать число в развернутой форме и вычислить его значение.
4 3 2 1 0
110012 10 = 1*24 + 1*23 + 0*22 + 0*21 + 1*20 = 16 + 8 + 1 = 2510
1 0
31 8 10 = 3*81 + 1*80 = 24 + 1 = 2510
1 0
19 16 10 = 1*161 + 9*160 = 16 + 9 = 2510

Десятичная
перевод дробных чисел
Для перевода дробного числа, нужно сначала перевести целую часть, а потом дробную и записать число. Целую часть переводим как обычно, а дробную умножаем на ту систему, в которую переводим, и записываем столько знаков после запятой, сколько просят в задаче. Если в задачи не указано количество знаков, которые надо записать, то записываем три знака после запятой.
12,51 10 2 = 1100,1002
2
12 6 2
0 6 3 2
0 2 1
1
0,51 * 2 1
0,02 * 2 0
0,04 * 2 0
0,08 * 2 0

Десятичная
перевод дробных чисел
17,5110 8 = 21,40638
8
2
1
0,51 * 8 4
0,08 * 8 0
0,64 * 8 6
0,4 * 8 3
17,5110 16 = 11,82816
16
1
1
0,51 * 16 8
0,16 * 16 2
0,56 * 16 8

Десятичная
перевод дробных чисел
Для перевода дробного числа в десятичную систему из любой другой, нужно это число записать в развернутой форме и вычислить его значение.
3 2 1 0 -1 -2 -3
1100,1002 10 =1*23+1*22+0*21+0*20+1*2-1+0*2-2+0*2-3 =8 +4 +0,5 = 12,510
1 0 -1 -2 -3 -4
21,40638 10 =2*81+1*80+4*8-1+0*8-2+6*8-3+3*8-4 =16+1+0,5+0,01+0,0007=17,510710
1 0 -1 -2 -3
11,82816 10=1*161+1*160+8*16-1+2*16-2+8*16-3 =16+1+0,5+0,007+0,002=17,50910

Двоичная
Для того чтобы число перевести из двоичной системы счисления в восьмеричную, надо разбить число с права на лево на триады, выписать каждую триаду и развернуть. Если не хватает цифр до триады дописать 0.
10011112 8= 1178
2 1 0
0012=0*22 +0*21 +1*20 =18
2 1 0
0012=0*22 +0*21 +1*20 =18
2 1 0
1112=1*22 +1*21 +1*20 =78

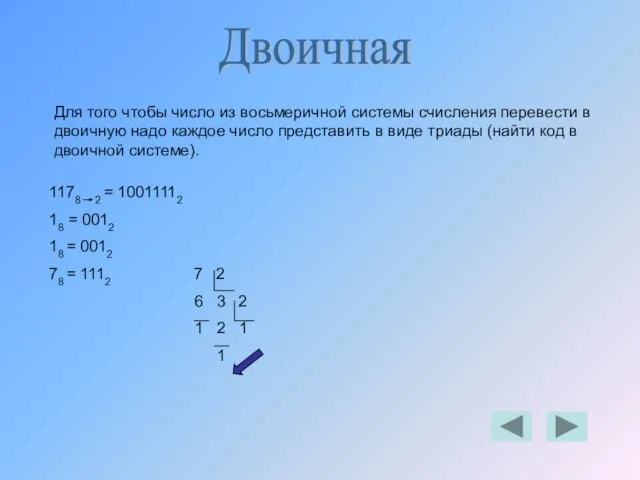
Двоичная
Для того чтобы число из восьмеричной системы счисления перевести в двоичную надо каждое число представить в виде триады (найти код в двоичной системе).
1178 2 = 10011112
18 = 0012
18 = 0012
78 = 1112 7 2
6 3 2
1 2 1
1

Двоичная
Для того чтобы число из двоичной системы счисления перевести в шестнадцатеричную, надо разбить с права на лево число на тетрады и развернуть каждую.
10011112 16= 4F16
3 2 1 0
01002= 0*23 +1*22 + 0*21 + 0*20 = 416
3 2 1 0
11112= 1*23 +1*22 +1*21 +1*20 =1516=F16

Двоичная
Для того чтобы число из шестнадцатеричной системы счисления перевести в двоичную, надо каждую цифру представить в виде тетрады (найти код в двоичной системе).
4F16 2=10011112
416= 01002 4 2
4 2 2
0 2 1
0
F16=1516 = 11112 15 2
14 7 2
1 6 3 2
1 2 1
1

Двоичная
перевод дробных чисел
Чтобы дробное число перевести из двоичной системы счисления в восьмеричную, надо целую часть разбить с права на лево, а дробную с лева на право на триады, выписать каждую триаду и развернуть.
110111,01101112 8= 67,3348
1102 = 68
1112 = 78
0112 = 38
0112 = 38
1002 = 48

Двоичная
перевод дробных чисел
Для того чтобы дробное число из двоичной системы счисления перевести в шестнадцатеричную, надо целую часть с права на лево, а дробную часть с лева на право разбить на тетрады, выписать каждое число и развернуть.
110111,01101112 16= 37,6E16
00112 =316
01112 =716
01102 =616
11102 =1416 =E16

Двоичная
перевод дробных чисел
Для того чтобы дробное число из восьмеричной системы счисления перевести в двоичную, нужно каждое число представить в виде триады (найти его код). Если получается число, где количество цифр меньше трех, впереди дописываем нули.
67,3348 2= 110111,01101112
68 =1102
78 =1112
38 =0112
38 =0112
48 =1002

Двоичная
перевод дробных чисел
Для того чтобы дробное число из шестнадцатеричной системы счисления перевести в двоичную, надо каждое число представить в виде тетрады (найти его код). Если количество цифр в числе получается меньше четырех, впереди дописываем нули.
37,6E16 2= 110111,01101112
316 = 00112
716 = 01112
616 = 01102
E16 =1416 =11102

Арифметические операции в разных системах счисления
Двоичная
Восьмеричная
Шестнадцатеричная

Двоичная
Примеры
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 =10
Таблица сложения одноразрядных двоичных чисел
1 1 1 1
1101001
1111
11110002
1 1 1 1 1 1
1110011
1111
100000102

Двоичная
Таблица вычитания одноразрядных двоичных чисел
0 – 0 = 0
0 – 1 = 11
1 – 0 = 1
1 – 1 = 0
Примеры
1 2 2
1110011 110111
1111 1101
11001002 1010102

Двоичная
Таблица умножения однорадрядных двоичных чисел
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1
Примеры
110111 1111011
1101 111
110111 1111011
110111 1111011
110111 1111011
10110010112 11010111012

Двоичная
Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.
Примеры
110111 1101 1101101 10101
100,00112 10101 101,0012
11000 11001
1101 10101
10110 100
1101
1001

Восьмеричная
Для выполнения арифметических действий в восьмеричной системе счисления нужно помнить, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.
Примеры
Сложение
157 37
67 25
2468 648

Восьмеричная
Вычитание
157 37
67 25
708 128
Умножение
157 37
67 25
1411 303
1232 76
137318 12638

Шестнадцатеричная
Для выполнения арифметических действий в шестнадцатеричной системе счисления нужно помнить, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.
Примеры
Сложение
9А5 FFFF
В9 1
А5Е16 1000016

Шестнадцатеричная
Вычитание
9A5 1996
B9 BABA
8EC16 BEDC16
Умножение
9A5 FFFF
B9 1
56CD FFFF16
6A17
6F83D16

Представление чисел в компьютере
Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм:
Модуль числа записать в прямом коде в n двоичных разрядах.
Получить обратный код числа, для этого значения всех битов инвертировать (все единицы заменить на нули и все нули заменить на единицы).
К полученному обратному коду прибавить единицу.
Рассмотрим Алгоритм на примере
Выполнить арифметическое действие 2010 – 6010 в 16-ти разрядном компьютерном представлении.
Представление чисел в формате с фиксированной запятой

Решение:
Переведем 20 из десятичной системы счисления в двоичную и запишем ее прямой код.
У положительного числа нет обратного и дополнительного кода.
2010 = 00000000000101002
2) Найдем прямой, обратный и дополнительный код 6010.
6010 = 00000000001111002 – прямой код
11111111110000112 – обратный код
11111111110001002 – дополнительный код
Просуммируем прямой код положительного с дополнительным кодом отрицательного.
00000000000101002
11111111110001002
11111111110110002

4) Инвертируем полученный дополнительный код.
00000000001001112
5) К полученному прибавили 1.
00000000001010002
6) Переведем в десятичную систему счисления и припишем знак
отрицательного числа.
1010002 = - 4010
Ответ: - 4010

Представление чисел в формате с плавающей запятой
Число с плавающей запятой может быть любым. Так число А может быть представлено в виде:
А = m * q n
m – мантисса числа
q – основание системы счисления
n – порядок числа
Мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля.
Например, число 555,55 будет иметь вид 0,55555 * 103

Пример задачи в формате с плавающей запятой
Представьте число 158,25010 в 4-х байтовой разрядной сетке.
Переведем число в двоичную систему счисления.
158,25010 = 10011110,012
Запишем число в виде нормальной мантиссы.
А = 10011110,01 * 10
А = 0,1001111001 * 108
А = 0,1001111001 * 101000
Представим число в 4-х байтовой разрядной сетке.
0 0 0 0 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0
Знак порядка
Порядок
Знак мантиссы
Мантисса

Арифметические операции с числами
в формате с плавающей запятой
При сложении чисел в формате с плавающей запятой, порядки выравниваются, а полученные мантиссы складываются.
0,1 * 23 + 0,1 * 25 = 0,001 * 25 + 0,1 * 25 = 0,101 * 25
При вычитании порядки выравниваются, а полученные мантиссы вычитаются.
0,1 * 26 - 0,1 * 23 = 0,1 * 26 – 0,001 * 26 = 0,099 * 26 = 0,99 * 25
При умножении чисел в формате с плавающей запятой порядки складываются, а мантиссы перемножаются.
(0,1 * 23) * (0,1 * 25) = 0,01 * 28 = 0,1 * 27
При делении из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя.
(0,1 * 26) / (0,1 * 23) = 1 * 22 = 0,1 * 23

Формы мышлния. Алгебра высказываний
В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «истина» (1) и «ложь» (0).
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквиволенция
Пример
решения
задачи
Важное

Инверсия
(логическое отрицание)
А , А
Инверсия логической переменой истина, когда само высказываний ложна и наоборот.
А А
1 0
0 1
Таблица истинности
1
0
Инвертор
Логическая схема

Конъюнкция
(логическое умножение)
& , ^ , и
Конъюнкция 2-х логических переменных истина тогда, когда оба высказывания истинны, в других случаях всегда ложна.
А В А ^ В
0 0 0
0 1 0
1 0 0
1 1 1
&
А
В
А^В
Конъюнктор
Таблица истинности
Логическая схема

Дизъюнкция
(логическое сложение)
V , или
Дизъюнкция 2-х логических переменных ложна тогда, когда оба высказывания ложны, в других случаях всегда истина.
А В А v В
0 0 0
0 1 1
1 0 1
1 1 1
1
А
В
А v В
Таблица истинности
Дизъюнктор
Логическая схема

Импликация
(логическое следование)
- > , =>
Импликация 2-х логических переменных ложна тогда, когда первое высказывание истина, а второе высказывание ложь, в других случаях высказывание истина.
А В А => В
0 0 1
0 1 1
1 0 0
1 1 1
А => В = А v В
А
В
А
А v В
v
Таблица истинности
Логическая схема импликатора

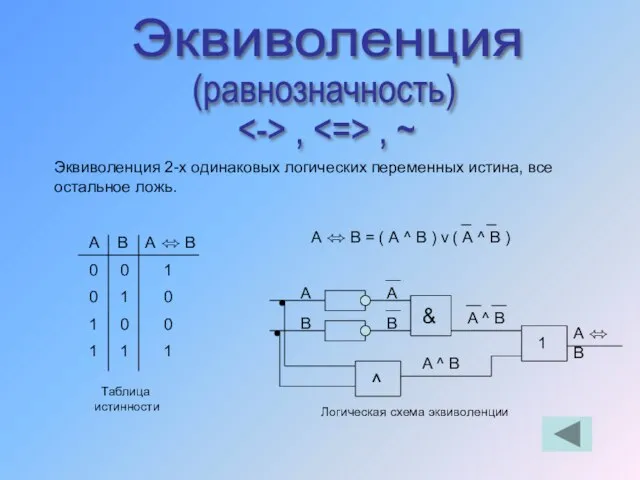
Эквиволенция
(равнозначность)
<-> , <=> , ~
Эквиволенция 2-х одинаковых логических переменных истина, все остальное ложь.
А В А ⬄ В
0 0 1
0 1 0
1 0 0
1 1 1
А ⬄ В = ( А ^ В ) v ( А ^ В )
А
В
А
В
^
&
1
А ^ В
А ^ В
А ⬄ В
Таблица истинности
Логическая схема эквиволенции

Важное
Высказывания выполняются только в такой последовательности и только в такой:
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквиволенция

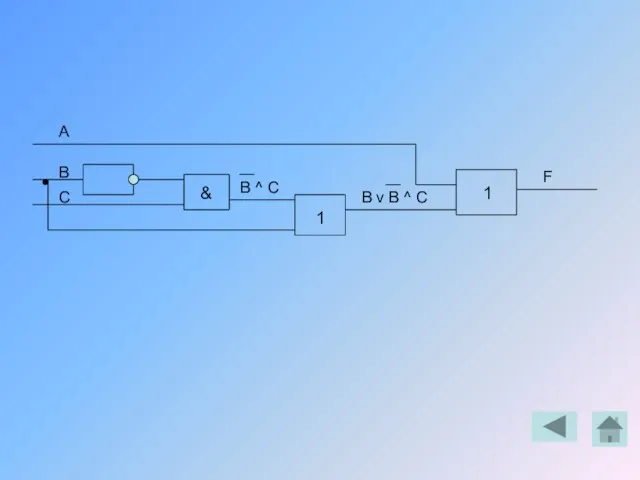
Пример решения задачи
Построить таблицу истинности и логическую схему для уравнения
F = A v (B v B ^ C).
А В С В В ^ C B v B ^ C F
0 0 0 1 0 0 0
0 0 1 1 1 1 1
0 1 0 0 0 1 1
0 1 1 0 0 1 1
1 0 0 1 0 0 1
1 0 1 1 1 1 1
1 1 0 0 0 1 1
1 1 1 0 0 1 1

А
В
С
&
1
1
В ^ C
B v B ^ C
F

Логические законы и правила
преобразования логических выражений
Закон тождества: А = А Закон непротиворечия: А & А = 0
Закон исключенного третьего: А v А = 1
Закон двойного отрицания: А = А
Законы де Моргана: А v В = А & В
А & В = А v В
Закон коммутативности: логическое умножение А & B = B & A
логическое сложение А v B = B v A
Закон ассоциативности: (А & B) & C = A & (B & C)

Логические законы и правила
преобразования логических выражений
Закон дистрибутивности: дистрибутивность умножения относительно
сложения (А & B) v (A & C) = A & (B v C)
дистрибутивность сложения относительно
умножения (A v B) & (A v C) = A v (B & C)
Правила замены операции импликации: А => В = А v B
A => B = B => A
Правила замены операции эквивалентности: А ⬄ B = (A & B) v (A & B)
A ⬄ B = (A v B) & (A v B)
A ⬄ B = (A => B) & ( B => A)

Совершенная дизъюнктивная нормальная форма
Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые.
Всякую дизъюнкцию элементарных конъюнкций назовем дизъюнктивной нормальной формой (ДНФ).
Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все конъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз, возможно с отрицанием.

Алгоритм получения СДНФ
по таблице истинности
Отметить те строки таблицы истинности, в последнем столбце которых стоят 1
X Y F ( x, y )
0 0 0
0 1 1 *
1 0 1 *
1 1 1
Выписать для каждой отмеченной строки конъюнкцию всех переменных следующим образом:
если значение некоторой переменной в данной строке равно 1, то в конъюнкцию включать саму эту переменную, если равна 0, то ее отрицание.
2: X ^ Y
3: X ^ Y

3) Все полученные конъюнкции связать в дизъюнкцию
F ( x, y ) = ( x ^ y ) v ( x ^ y )
X Y Y X ^ Y X X ^ Y ( X ^ Y ) v ( X ^ Y )
0 0 1 0 1 0 0
0 1 0 0 1 1 1
1 0 1 1 0 0 1
1 1 0 0 0 0 0
Ч. Т. Д.

Совершенная конъюнктивная нормальная форма
Элементарной конъюнкцией называется конъюнкция нескольких переменных взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые.
Всякую конъюнкцию элементарных дизъюнкций назовем конъюнктивной нормальной формой (КНФ).
Совершенной конъюнктивной нормальной формой (СКНФ) называется КНФ, в которой нет одинаковых элементарных дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз, возможно с отрицанием.

Алгоритм получения СКНФ
по таблице истинности
1) Отметить те строки таблицы истинности, в последнем столбце которых стоит 0.
X Y F ( x, y )
0 0 0 *
0 1 1
1 0 1
1 1 0 *
Выписать для каждой отмеченной строки дизъюнкцию всех переменных следующим образом:
если значение некоторой переменной в данной строке равно 0, то в дизъюнкцию включать саму эту переменную, если 1, то ее отрицание.
1: X v Y
4: X v Y

3) Все полученные дизъюнкции связать в конъюнкцию.
F ( x, y ) = ( x v y ) ^ ( x v y )
( x v y ) ^ ( x v y ) = x x + x y + x y + y y = x y + x y
( x ^ y ) v ( x ^ y )
X Y Y X ^ Y X X ^ Y ( X ^ Y ) v ( X ^ Y )
0 0 1 0 1 0 0
0 1 0 0 1 1 1
1 0 1 1 0 0 1
1 1 0 0 0 0 0
Ч. Т. Д.

Тест
проверим ваши знания
Приступить
МЕНЮ

Вопрос №1
Переведите 3 Мбайт в биты. В ответ запишите сумму цифр получившегося числа.

Вопрос №2
У племени в алфавите 24 буквы и 8 цифр. Сколько разрядов минимум им понадобится чтобы закодировать каждый символ?

Вопрос №3
Текст записанный с помощью 32-символьного алфавита занимает 10 секторов на односторонней дискете и весит 300 Кбайт. Дискета содержит 40 дорожек и 15 секторов. Сколько символов содержит этот текст?

Вопрос №4
В корзине лежат 32 клубка шерсти, среди них 4 красных. Сколько информации несет сообщение о том, что достали красный клубок шерсти?

Вопрос №5
Переведите число 11111011 из двоичной системы счисления в восьмеричную.

Вопрос №6
Переведите число 197,51 из десятичной системы счисления в двоичную.

Вопрос №7
Переведите число 110011,1101 из двоичной системы счисления в шестнадцатеричную.

Вопрос №8
Переведите число 10100010,01001 из двоичной системы счисления в десятичную.

Вопрос №9
Произведите умножения чисел 101 и 11 в двоичной системе счисления.

Вопрос №10
Найдите разность чисел 1996 и ВАВА в шестнадцатеричной системе счисления.

Вопрос №11
Выполните арифметическое действие 300010 – 500010 в 16-ти разрядном компьютерном представлении. Ответ запишите в двоичной системе счисления.

Вопрос №12
Представьте число 250,187510 в формате с плавающей запятой в 4-х байтовой разрядной сетке. Запишите в ответ количество единиц в полученном числе.

Вопрос №13
Постройте таблицу истинности для уравнения F =(x & y) v z. В ответ запишите последовательность полученную для переменной F.

Вопрос №14
Получите СДНФ по таблице истинности. В ответ запишите получившуюся последовательность цифр. X Y Z F
1 1 0 1
1 0 1 0
1 1 1 1

Вопрос №15
Получите СКНФ по таблице истинности. В ответ запишите получившуюся последовательность цифр.
X Y Z F
1 0 0 1
0 1 0 1
0 1 1 0