Information

By the end of this lecture you should:
Understand the notions of natural frequency of an oscillating system and the driving frequency of a system
Be able to define resonance
Give some real examples of resonance
Understand what is meant by damping and be able to give examples in which damping occurs
Have clear, useful notes from the material presented
Energy in SHM

Energy in SHM
Kinetic energy :
Potential energy:
The energy required to extend the mass on a spring by a displacement x is stored in the spring and is called the potential energy
Hence the total energy is given by:

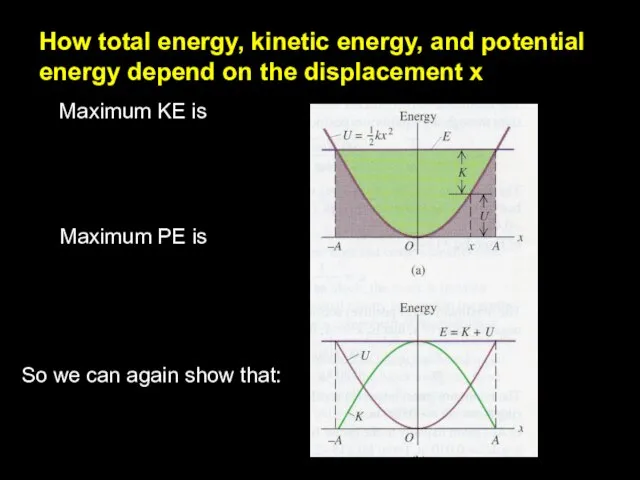
How total energy, kinetic energy, and potential energy depend on the displacement x
Maximum KE is
Maximum PE is
So we can again show that:

Example 1
A mass of 500 g is in equilibrium on the end of a vertical spring of force constant k = 200 N m-1 .
It is then pulled downwards a distance x = 2.00 cm and released so that it oscillates with SHM.
Find the following at the point when the mass has travelled half-way towards the equilibrium position
a) the velocity
b) the acceleration
c) the total energy
d) the kinetic energy
e) the potential energy

SHM and circular motion
P moves in circular motion about O. If we illuminate this motion, P makes a shadow on the screen. As P rotates, the shadow of P on the screen moves with simple harmonic motion (SHM). We call this the projection of P on the y axis

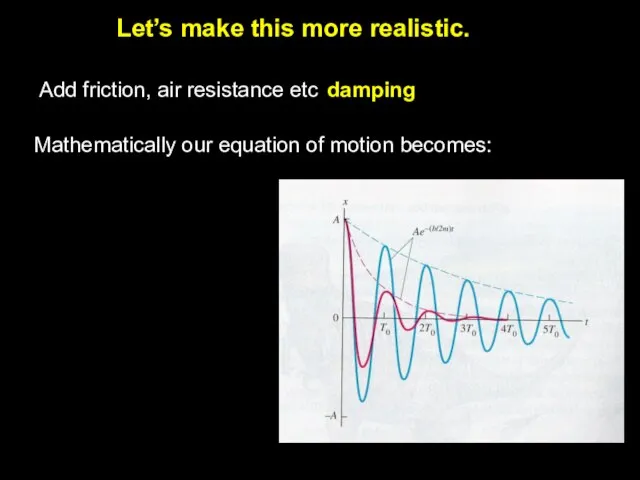
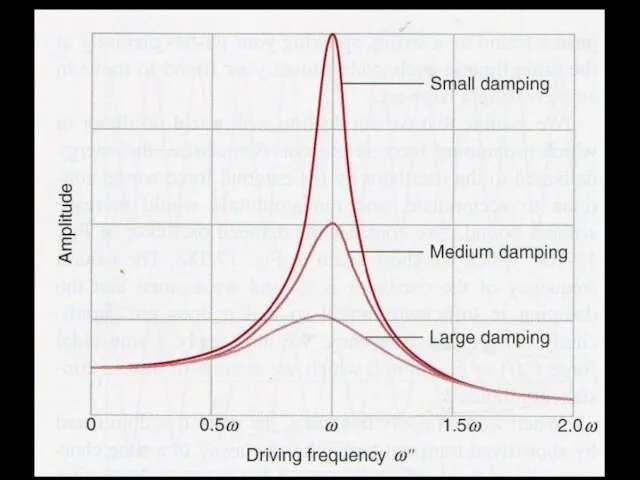
Let’s make this more realistic.
Add friction, air resistance etc damping
Mathematically our equation of motion becomes:

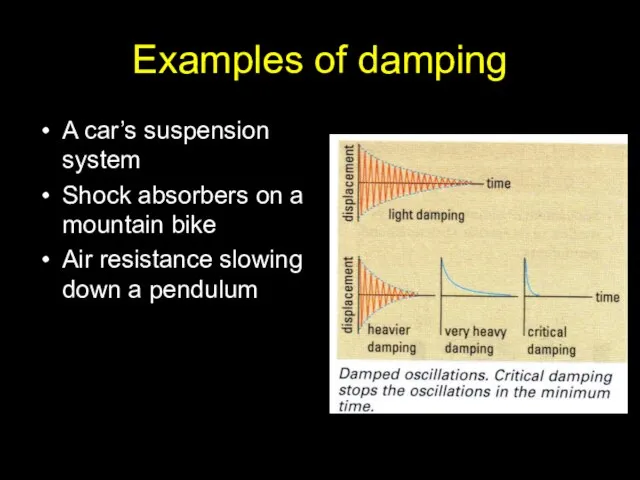
Examples of damping
A car’s suspension system
Shock absorbers on a mountain bike
Air resistance slowing down a pendulum

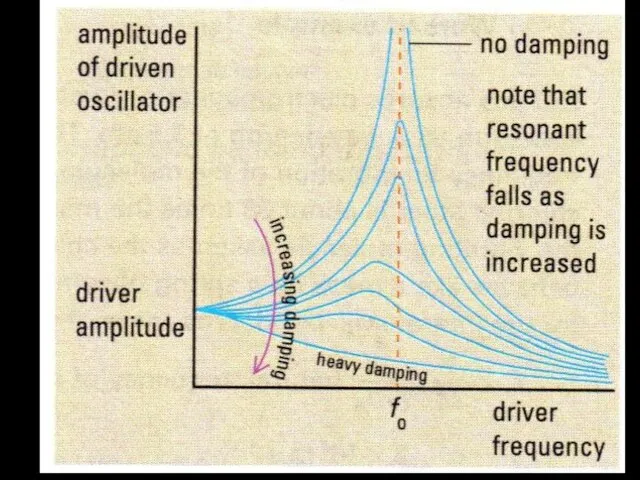
Spring system with ‘driving force’
Apply a periodic force to a damped system that can oscillate with SHM of “natural” frequency.
The periodic force is given by
And the equation of motion becomes:

Example 2
A free swing is a lightly damped system.
If a girl starts swinging from a amplitude of x= 50 cm with a frequency of 0.5Hz, calculate the maximum damping force if the damping coefficient is 58.3 Nsm-1

Examples of resonance
Pushing a child on a swing
Singing or playing a musical instrument
Nuclear Magnetic Resonance
Bridge subject to wind or earthquake

LECTURE CHECK LIST
Simple Harmonic Motion (SHM)
READING Adams and Allday: 3.32, 3.33, 3.34.
Understand PE and KE and total energy for SHM
Be able to perform calculations to find the amplitude, period, frequency and angular frequency of objects performing SHM in a variety of situations
Be able to perform calculations involving PE KE acceleration velocity
displacement and energy.
Understand the links between SHM and circular motion