Содержание
- 2. Пусть рекурсивный предикат D(z: u) принадлежит кольцу (3.36), т.е. D = Aj для некоторого j. Логическая
- 3. Рекурсивное кольцо предикатов представим в виде: A ≡ K(A1, A2,…, An, E1, E2,…, Es) (3.42) E1,
- 4. 3. Язык исчисления вычислимых предикатов (продолжение 3)
- 5. Однозначность предикатов Лемма 3.17. Оператор суперпозиции (3.16), параллельный оператор (3.19) или условный оператор (3.20) является однозначным,
- 6. Пусть D(u: v) ⎯ рекурсивный предикат кольца, т.е. D = Aj для некоторого j. Допустим, истинны
- 7. Лемма 3.19. Вызов C(…), где C ⎯ переменная предикатного типа, является однозначным, если для каждого вызова
- 8. Имеется рекурсивных дерево колец (теорема 3.1). Для колец, являющихся листьями, однозначность следует из леммы 3.18. Применяется
- 9. 4. Система правил доказательства корректности операторов 4.1. Правила для однозначной спецификации
- 10. Предикат B(x, y) корректен относительно [PB(x), QB(x, y)], если: P(x) ⇒ [Lk(x, y) ⇒ Q(x, y)]
- 11. Теорема 2.1 тождества спецификации и программы P(x) { S (x, y) ♦k } Q(x, y) (2.1)
- 12. Правила для параллельного оператора {P(x)} A || B {Q(x, y, z)} (4.17) {PA(x)} A {QA(x, y)},
- 13. Правила для оператора суперпозиции {P(x)} A; B {Q(x, y)} (4.18) {PA(x)} A {QA(x, z)}, {PB(z)} B
- 14. Пусть истинны P(x) и Q(x, y). Докажем истинность ∃z.(LS(A)(x, z) & LS(B)(z, y)). Из истинности предусловия
- 15. Правила для условного оператора {P(x)} if (C) A else B {Q(x, y)} (4.19) {PA(x)} A {QA(x,
- 16. Пусть истинны P(x) и Q(x, y). Докажем истинность формулы C ⇒ LS(A)(x, y). Пусть истинно C.
- 17. 4. Система правил доказательства корректности программы 4.2. Правила для общего случая
- 18. Правила для параллельного оператора {P(x)} A || B {Q(x, y, z)} (4.11) {PA(x)} A {QA(x, y)},
- 19. Из истинности предусловия P(x) по правилу RP1 следует истинность PA(x) и PB(x). Далее, по правилу E2
- 20. Правила для оператора суперпозиции {P(x)} A; B {Q(x, y)} (4.12) {PA(x)} A {QA(x, z)}, {PB(z)} B
- 21. Из истинности предусловия P(x) по правилу RS1 следует истинность формул PA(x) и ∀z (QA(x, z) ⇒
- 22. Докажем выводимость постусловия Q(x, y) из LS(A; B)(x, y). Пусть LS(A; B)(x, y) истинно, т.е. истинна
- 23. Правила для условного оператора {P(x)} if (C) A else B {Q(x, y)} (4.13) {PA(x)} A {QA(x,
- 24. Допустим, что условие C истинно. Из истинности предусловия P(x) по правилу RC1 следует истинность PA(x). По
- 25. 4. Система правил декомпозиции доказательства корректности операторов 4.3. Правила для однозначной спецификации
- 26. Правила для параллельного оператора Для параллельного оператора A(x: y) || B(x: z) определим правила: Правило FP1.
- 27. Правила для условного оператора Для условного оператора if (C) A(x: y) else B(x: y) определим правила:
- 28. Правила для оператора суперпозиции Для оператора суперпозиции A(x: z); B(x, z: y) определим правила: более общего
- 29. Правила для нерекурсивного вызова Пусть имеется нерекурсивный вызов предиката A(x: y) со спецификацией: {P(x)} A(x: y)
- 30. 4. Система правил декомпозиции доказательства корректности операторов 4.4. Правила для общего случая
- 31. Декомпозиция для параллельного оператора {P(x)} B(x: y) {Q(x, y)} Corr(B, P, Q) ≅ P(x) ⇒ [LS(B(x,
- 32. Декомпозиция для условного оператора {P(x)} B(x: y) {Q(x, y)} Corr(B, P, Q) ≅ P(x) ⇒ [LS(B(x,
- 33. Декомпозиция для оператора суперпозиции Рассмотрим спецификацию оператора суперпозиции в виде тройки Хоара: {P(x)} A; B {Q(x,
- 34. Задачи верификации и синтеза на примере оператора суперпозиции A(x: y) ≡ pre P(x) { B(x: z);
- 35. 5. Построение языка предикатного программирования. Методы доказательства корректности предикатных программ
- 36. P(x) ⇒ [ LS(S)(x, y) ⇒ Q(x, y) ] & ∃y. LS(S)(x, y) (4.1) P(x) &
- 37. Язык P1: подстановка определения предиката на место вызова Подстановка определения предиката A(x: y) ≡ K(x: y)
- 38. Язык P2: оператор суперпозиции и параллельный оператор общего вида Операторы { A(…); B(…) }; C(…) и
- 39. LS(B1(x: z1); B2(z1: z2);...; Bj(zj-1: zj);...; Bn(zn-1: y)) ≡ ∃ z1, z2, …, zn-1.LS(B1(x: z1)) &
- 40. Параллельный оператор общего вида P(x){B1(x: y1) || B2(x: y2)||...||Bj(x: yj)||...||Bn(x: yn)}Q(x, y) (5.7) x, y =
- 41. Правило опускания скобок: {A(…); B(…)} || C(…) → A(…); B(…) || C(…). A(x: y); {B(z: t)
- 42. Язык P2: другое обобщение оператора суперпозиции B(x: z); C(x, z: y) ⎯ обобщение оператора суперпозиции. P(x)
- 43. B1(x: x1, z, t1) ≡ PB(x) {B(x: z, t1) || x1 = x} QB(x, z, t1)
- 44. Правило RS5. P(x) ├ PB(x) & ∀z, t (QB(x, z, t) ⇒ PC(x, z)) Правило RS6.
- 45. Язык P3: выражения Функциональная форма. Предикат A(t: z). z = A(t) ≅ A(t: z) |z| =
- 46. D(x, z: u) ≡ P(x, z) {C(A(x), B(z): u)} Q(x, z, u) (5.15) E(x, z: y,
- 47. Правило RS7. P(x, z) ├ PA(x) & PB(z) & PC(A(x), B(z)) Правило RS8. P(x, z) &
- 48. Правило LS8. P(x, z) ├ PA(x) & PB(z). Правило LS9. P(x, z) & Q(x, z, u)├
- 50. Скачать презентацию
Слайд 2Пусть рекурсивный предикат D(z: u) принадлежит кольцу (3.36), т.е. D = Aj для некоторого j.
Пусть рекурсивный предикат D(z: u) принадлежит кольцу (3.36), т.е. D = Aj для некоторого j.

LS(D(z: u)) ≅ (z, u)∈pr(j, ∪m≥0Gm) (3.40)
Систему (3.36) определений кольца предикатов запишем в векторном виде: A ≡ K(A), где A = (A1, A2,…, An), K = (K1, K2,…, Kn). Определим цепь векторов предикатов {Am}m≥0:
A0 ≡ Ф, Am+1 ≡ K(Am), m ≥ 0, (3.41)
где Ф ≅ (F, F, …, F) ⎯ вектор тотально ложных предикатов. Цепь {Am}m≥0 соответствует цепи (3.39) вектор-графиков {Gm}m≥0, поскольку Gm = (Gr(Am1), Gr(Am2),…, Gr(Amn)).
G0 = ∅, Gm+1 = V(Gm), m ≥ 0 (3.39)
Ai(xi: yi) ≡ Ki(xi: yi); i = 1…n; n > 0, (3.36)
Слайд 3Рекурсивное кольцо предикатов представим в виде:
A ≡ K(A1, A2,…, An, E1, E2,…, Es) (3.42)
E1, E2,…, Es, s > 0, ⎯ предикаты, используемые в
Рекурсивное кольцо предикатов представим в виде:
A ≡ K(A1, A2,…, An, E1, E2,…, Es) (3.42)
E1, E2,…, Es, s > 0, ⎯ предикаты, используемые в

Лемма 3.16. Пусть предикаты E1, E2,…, Es, используемые в системе (3.42), обладают свойством согласованности. Тогда рекурсивные предикаты A1, A2,…, An кольца (3.42) обладают свойством согласованности.
Слайд 43. Язык исчисления вычислимых предикатов
(продолжение 3)
3. Язык исчисления вычислимых предикатов
(продолжение 3)

Слайд 5 Однозначность предикатов
Лемма 3.17. Оператор суперпозиции (3.16), параллельный оператор (3.19) или условный оператор
Однозначность предикатов
Лемма 3.17. Оператор суперпозиции (3.16), параллельный оператор (3.19) или условный оператор

Лемма 3.18. Пусть имеется рекурсивное кольцо предикатов (3.42). Кроме рекурсивных предикатов A1, A2,…,An в правых частях определений кольца предикатов используются предикаты E1, E2,…, Es. Предположим, что предикаты E1, E2,…, Es являются однозначными. Если аргумент определения кольца имеет предикатный тип, то предикат, являющийся значением аргумента, считается однозначным. Тогда рекурсивные предикаты A1, A2,…,An кольца (3.42) являются однозначными.
Доказательство. Из-за ограничений на сложные формы рекурсии предикат, являющийся значением аргумента, не может входить в кольцо предикатов. Поэтому можно считать, что такой предикат находится среди E1, E2,…, Es.
A ≡ K(A1, A2,…, An, E1, E2,…, Es) (3.42)
Слайд 6 Пусть D(u: v) ⎯ рекурсивный предикат кольца, т.е. D = Aj для некоторого j.
Пусть D(u: v) ⎯ рекурсивный предикат кольца, т.е. D = Aj для некоторого j.

Элемент A0 является вектором однозначных предикатов, поскольку тотально ложный предикат F является однозначным. Допустим, по индуктивному предположению, Am-1 является вектором однозначных предикатов. Докажем это свойство для Am. В правой части каждого определения из Am используется оператор суперпозиции, параллельный оператор или условный оператор. Вызываемые предикаты в правой части: Am-11, Am-12,…, Am-1n и E1, E2,…, Es ⎯ однозначны. Однозначность компонент Am следует из леммы 3.17. □
Базисные предикаты ConsPred и ConsArray не являются однозначными. В двух разных исполнениях вызова ConsPred(x, B: A) (при совпадающих x и B) в качестве значения переменной A будут получены разные имена.
Слайд 7 Лемма 3.19. Вызов C(…), где C ⎯ переменная предикатного типа, является однозначным,
Лемма 3.19. Вызов C(…), где C ⎯ переменная предикатного типа, является однозначным,

Теорема 3.2. Допустим, всякий базисный предикат языка CCP, кроме ConsPred и ConsArray, является однозначным. Пусть имеется программа на языке CCP, и ее исполнение реализуется вызовом предиката D(u: v), причем в наборе v нет переменных предикатного типа. Тогда предикат D является однозначным.
Доказательство. Сначала доказательство проводится для программы, в которой нет переменных предикатного типа.
Рассмотрим случай, когда программа не содержит рекурсивно определяемых предикатов. Если предикат D ⎯ базисный, то его однозначность гарантируется условием теоремы. Пусть предикат D имеет определение в виде оператора суперпозиции, параллельного оператора или условного оператора. В соответствии с леммой 3.17 достаточно установить однозначность предикатов B и C, вызываемых в правой части определения. Если эти предикаты ⎯ базисные, то их однозначность является условием теоремы. Если один из них ⎯ определяемый, то его полное замкнутое определение ⎯ программа меньшего размера. Далее по индукции.
Слайд 8Имеется рекурсивных дерево колец (теорема 3.1). Для колец, являющихся листьями, однозначность следует
Имеется рекурсивных дерево колец (теорема 3.1). Для колец, являющихся листьями, однозначность следует

Допустим, в программе П имеются переменные предикатного типа. Обозначим через SUBS(П) набор предикатов, являющийся объединением множеств заместителей для всех переменных предикатного типа в программе П. Для набора предикатов M из П обозначим через П[M] минимальную программу, являющуюся частью П и содержащую определения предикатов набора M. Пусть П0 = П, Пj+1 = Пj[SUBS(Пj)], j=0, 1, 2, … . В теореме 3.1 доказано, что для некоторого k программа Пk ≠ ∅, а Пk+1 = ∅. Программа Пk не содержит переменных предикатного типа. Однозначность предикатов программы Пk доказана выше. Тогда предикаты B1, B2,…, Bn, входящие в SUBS(Пk-1), являются однозначными. В соответствии с леммой 3.19 любой вызов вида C(…) в программе Пk-1, где C ⎯ переменная предикатного типа, является однозначным. Доказательство теоремы, представленное выше, обобщается для программы Пk-1, поскольку согласно принятым ограничениям вызов вида C(…) не может участвовать в рекурсии. Доказательство теоремы для произвольной программы Пi, i = k-1, …, 0, проводится по индукции. □
Слайд 94. Система правил доказательства корректности операторов 4.1. Правила для однозначной спецификации
4. Система правил доказательства корректности операторов 4.1. Правила для однозначной спецификации

Слайд 10Предикат B(x, y) корректен относительно [PB(x), QB(x, y)], если:
P(x) ⇒ [Lk(x, y) ⇒ Q(x, y)] &
Предикат B(x, y) корректен относительно [PB(x), QB(x, y)], если:
P(x) ⇒ [Lk(x, y) ⇒ Q(x, y)] &
![Предикат B(x, y) корректен относительно [PB(x), QB(x, y)], если: P(x) ⇒ [Lk(x,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/432424/slide-9.jpg)
P(x) ⇒ [LS(B(x, y)) ⇒ Q(x, y)] & ∃y. LS(B(x, y) (4.1)
Corr(B, P, Q) ≅ (4.1)
Правила для корректного оператора
Лемма 4.3. Пусть имеется оператор B со спецификацией в виде тройки Хоара {PB(x)} B {QB(x, y)}. Предполагается, что оператор B является корректным Тогда истинны следующие правила вывода:
Правило E1. PB(x) ├ ∃y. QB(x, y)
Правило E2. PB(x) ├ ∃y. LS(B(x, y))
Правило E3. PB(x) ├ LS(B(x, y)) ⇒ QB(x, y)
Слайд 11Теорема 2.1 тождества спецификации и программы P(x) { S (x, y) ♦k } Q(x, y) (2.1)
Оператор
Теорема 2.1 тождества спецификации и программы P(x) { S (x, y) ♦k } Q(x, y) (2.1)
Оператор

P(x) & Q(x, y) ⇒ LS(S(x, y)) (4.6)
Тогда программа (2.1) является корректной.
Лемма 2.8. В условиях теоремы 2.1 истинна ф-ла:
P(x) ⇒ (LS(S(x, y)) ≡ Q(x, y))
Лемма 2.9. Допустим, программа (2.1) является корректной, а ее спецификация ⎯ однозначной. Тогда истинна формула (4.6), т.е. LS(S(x, y)) выводима из спецификации.
Слайд 12Правила для параллельного оператора
{P(x)} A || B {Q(x, y, z)} (4.17)
{PA(x)} A
Правила для параллельного оператора
{P(x)} A || B {Q(x, y, z)} (4.17)
{PA(x)} A

Правило LP1. P(x) ├ PB(x) & PC(x)
Правило LP2. P(x) & Q(x, y, z) ├ QA(x, y).
Правило LP3. P(x) & Q(x, y, z) ├ QB(x, z).
Лемма 4.10. Пусть спецификация параллельного оператора (4.17) реализуема, операторы A и B однозначны в области предусловий и корректны, а их спецификации ⎯ однозначны. Если правила LP1, LP2 и LP3 истинны, то параллельный оператор (4.17) является корректным.
Доказательство. Операторы A и B ⎯ однозначны ⇒ оператор (4.17) однозначный. Поскольку спецификация оператора (4.17) реализуема, в соответствии с теоремой 2.1 достаточно доказать:
P(x) & Q(x, y, z) ⇒ LS(A || B)(x, y, z)
LS(A || B)(x, y, z) ≅ LS(A)(x, y) & LS(B)(x, z) (4.2)
Пусть истинны P(x) и Q(x, y, z). Докажем истинность LS(A)(x, y) и LS(B)(x, z). Из истинности предусловия P(x) по правилу LP1 следует истинность PA(x) и PB(x). По правилам LP2 и LP3 становятся истинными QA(x, y) и QB(x, z). Для предикатов A и B выполняются условия леммы 2.9. Поэтому истинны формулы:
PA(x) & QA(x, y) ⇒ LS(A)(x, y) PB(x) & QB(x, z) ⇒ LS(B)(x, z)
Посылки этих формул истинны ⇒ истинны LS(A)(x, y) и LS(B)(x, z). □
Слайд 13Правила для оператора суперпозиции
{P(x)} A; B {Q(x, y)} (4.18)
{PA(x)} A {QA(x, z)}, {PB(z)}
Правила для оператора суперпозиции
{P(x)} A; B {Q(x, y)} (4.18)
{PA(x)} A {QA(x, z)}, {PB(z)}

Правило LS1. P(x) ├ PA(x)
Правило LS2. P(x) & Q(x, y) & QA(x, z) ├ PB(z) & QB(z, y)
Лемма 4.11. Пусть спецификация оператора суперпозиции (4.18) реализуема, операторы A и B однозначны в области предусловий и корректны, а их спецификации ⎯ однозначны. Если правила LS1 и LS2 истинны, то оператор суперпозиции (4.18) является корректным.
Доказательство. Поскольку операторы A и B ⎯ однозначны, то и оператор суперпозиции (4.18) является однозначным. В соответствии с теоремой 2.1 для доказательства леммы достаточно доказать истинность формулы:
P(x) & Q(x, y) ⇒ LS(A; B)(x, y)
LS(A; B)(x, y) ≅ ∃z.(LS(A)(x, z) & LS(B)(z, y)) (4.1)
Слайд 14Пусть истинны P(x) и Q(x, y). Докажем истинность ∃z.(LS(A)(x, z) & LS(B)(z, y)). Из истинности предусловия P(x)
Пусть истинны P(x) и Q(x, y). Докажем истинность ∃z.(LS(A)(x, z) & LS(B)(z, y)). Из истинности предусловия P(x)

PB(z) & QB(z, y) ⇒ LS(B)(z, y)
Тогда истинна LS(B)(z0, y). В итоге, будет истинна формула ∃z.(LS(A)(x, z) & LS(B)(z, y)). □
Слайд 15Правила для условного оператора
{P(x)} if (C) A else B {Q(x, y)} (4.19)
{PA(x)} A {QA(x, y)},
Правила для условного оператора
{P(x)} if (C) A else B {Q(x, y)} (4.19)
{PA(x)} A {QA(x, y)},

Правило LC1. P(x) & Q(x, y) & C ├ PA(x) & QA(x, y)
Правило LC2. P(x) & Q(x, y) & ¬C ├ PB(x) & QB(x, y)
Лемма 2.12. Пусть спецификация условного оператора (4.19) реализуема, операторы A и B однозначны в области предусловий и корректны, а их спецификации ⎯ однозначны. Если правила LC1 и LC2 истинны, то условный оператор (4.19) является корректным.
Доказательство. Поскольку операторы A и B ⎯ однозначны, то и условный оператор (4.19) является однозначным. В соответствии с теоремой 2.1 для доказательства леммы достаточно доказать:
P(x) & Q(x, y) ⇒ LS( if (C) A else B ) (x, y)
LS(if (C) A else B)(x, y) ≅ (C ⇒ LS(A)(x, y)) & (¬C ⇒ LS(B)(x, y)) (4.3)
Слайд 16Пусть истинны P(x) и Q(x, y). Докажем истинность формулы C ⇒ LS(A)(x, y). Пусть истинно C.
Пусть истинны P(x) и Q(x, y). Докажем истинность формулы C ⇒ LS(A)(x, y). Пусть истинно C.

PA(x) & QA(x, y) ⇒ LS(A)(x, y)
Поскольку истинна посылка, то истинно LS(A)(x, y). Следовательно, доказана истинность формулы C ⇒ LS(A)(x, y). Истинность формулы ¬C ⇒ LS(B)(x, y) доказывается аналогично. □
Слайд 174. Система правил доказательства корректности программы 4.2. Правила для общего случая
4. Система правил доказательства корректности программы 4.2. Правила для общего случая

Слайд 18Правила для параллельного оператора
{P(x)} A || B {Q(x, y, z)}
Правила для параллельного оператора
{P(x)} A || B {Q(x, y, z)}

{PA(x)} A {QA(x, y)}, {PB(x)} B {QB(x, z)}
Правило RP1. P(x) ├ PA(x) & PB(x)
Правило RP2. QA(x, y), QB(x, z) ├ Q (x, y, z)
Лемма 4.4. Пусть предусловие P(x) истинно. Допустим, операторы A и B корректны. Если правила RP1 и RP2 истинны (т.е. правая часть доказуема из левой части для каждого правила), то параллельный оператор (4.11) является корректным.
Доказательство. В соответствии с формулой (4.1) достаточно доказать реализуемость LS(A || B) и выводимость постусловия Q(x, y, z) из LS(A || B).
LS(A || B) (x, y, z) ≅ LS(A)(x, y) & LS(B)(x, z).
Слайд 19Из истинности предусловия P(x) по правилу RP1 следует истинность PA(x) и PB(x).
Из истинности предусловия P(x) по правилу RP1 следует истинность PA(x) и PB(x).

Докажем выводимость постусловия Q(x, y, z) из LS(A)(x, y) & LS(B)(x, z). Допустим, истинна LS(A)(x, y) & LS(B)(x, z). Применим правило E3 для PA(x) и PB(x), истинность которых определена выше. Получаем истинность формул LS(A)(x, y) ⇒ QA(x, y) и LS(B)(x, z) ⇒ QB(x, z). Как следствие, будут истинны QA(x, y) и QB(x, z). Применяя правило RP2, получаем истинность постусловия Q(x, y, z). □
Слайд 20Правила для оператора суперпозиции
{P(x)} A; B {Q(x, y)} (4.12)
{PA(x)} A {QA(x, z)}, {PB(z)}
Правила для оператора суперпозиции
{P(x)} A; B {Q(x, y)} (4.12)
{PA(x)} A {QA(x, z)}, {PB(z)}

Правило RS1. P(x) ├ PA(x) & ∀z (QA(x, z) ⇒ PB(z))
Правило RS2. P(x) & ∃z (QA(x, z) & QB(z, y))├ Q(x, y)
Лемма 4.5. Пусть предусловие P(x) истинно. Допустим, операторы A и B корректны. Если правила RS1 и RS2 истинны, то оператор суперпозиции (4.12) является корректным.
Доказательство. В соответствии с формулой (4.1) достаточно доказать реализуемость LS(A; B)(x, y) и выводимость постусловия Q(x, y) из LS(A; B)(x, y).
LS(A; B)(x, y) ≅ ∃z.(LS(A)(x, z) & LS(B)(z, y)) .
Слайд 21Из истинности предусловия P(x) по правилу RS1 следует истинность формул PA(x) и
Из истинности предусловия P(x) по правилу RS1 следует истинность формул PA(x) и

Слайд 22Докажем выводимость постусловия Q(x, y) из LS(A; B)(x, y). Пусть LS(A; B)(x, y) истинно, т.е. истинна формула
Докажем выводимость постусловия Q(x, y) из LS(A; B)(x, y). Пусть LS(A; B)(x, y) истинно, т.е. истинна формула

Слайд 23Правила для условного оператора
{P(x)} if (C) A else B {Q(x, y)} (4.13)
{PA(x)} A {QA(x, y)}, {PB(x)}
Правила для условного оператора
{P(x)} if (C) A else B {Q(x, y)} (4.13)
{PA(x)} A {QA(x, y)}, {PB(x)}

Правило RC1. P(x) & C ├ PA(x)
Правило RC2. P(x) & ¬C ├ PB(x)
Правило RC3. P(x) & C & QA(x, y) ├ Q(x, y)
Правило RC4. P(x) & ¬C & QB(x, y) ├ Q(x, y)
Лемма 4.6. Пусть предусловие P(x) истинно. Допустим, операторы A и B корректны. Если правила RC1, RC2, RC3 и RC4 истинны, то условный оператор (4.13) является корректным.
Доказательство. Для оператора (4.13) необходимо доказать формулу (2.10). В ней дважды встречается подформула LS(if (C) A else B)(x, y), определяемая в виде: (C ⇒ LS(A)(x, y)) & (¬C ⇒ LS(B)(x, y)) (4.14)
Достаточно доказать реализуемость формулы (4.14) и выводимость постусловия Q(x, y) из (4.14).
Слайд 24Допустим, что условие C истинно. Из истинности предусловия P(x) по правилу RC1
Допустим, что условие C истинно. Из истинности предусловия P(x) по правилу RC1

Докажем выводимость постусловия Q(x, y) из формулы (2.14). Допустим, истинна формула (4.14). Пусть C истинно. Тогда истинно LS(A)(x, y). По правилу RC1 истинно PA(x). По правилу E3 истинна формула LS(A)(x, y) ⇒ QA(x, y), а значит и QA(x, y). Таким образом, истинна правая часть правила RC3. Тогда истинна левая часть правила, т.е. истинно постусловие Q(x, y). Доказательство истинности постусловия Q(x, y) для случая, когда C ложно, проводится аналогично с использованием правила RC4. □
Слайд 254. Система правил декомпозиции доказательства корректности операторов 4.3. Правила для однозначной спецификации
4. Система правил декомпозиции доказательства корректности операторов 4.3. Правила для однозначной спецификации

Слайд 26Правила для параллельного оператора
Для параллельного оператора A(x: y) || B(x: z) определим правила:
Правило FP1. R(x, y,
Правила для параллельного оператора
Для параллельного оператора A(x: y) || B(x: z) определим правила:
Правило FP1. R(x, y,

Правило FP2. R(x, y, z) ├ LS(B(x, z))
Лемма 7. Если истинны правила FP1 и FP2, то истинна формула:
R(x, y, z) ⇒ LS(A(x: y) || B(x: z))
Доказательство. Формула LS(A(x: y) || B(x: z)) эквивалентна LS(A(x: y)) & LS(B(x: z)). Поэтому достаточно доказать истинность двух формул:
R(x, y, z) ⇒ LS(A(x: y))
R(x, y, z) ⇒ LS(B(x: z))
Эти формулы эквивалентны правилам FP1 и FP2. □
P(x) & Q(x, y) ⇒ LS(S(x, y)) (4.6)
Слайд 27Правила для условного оператора
Для условного оператора if (C) A(x: y) else B(x: y) определим правила:
Правило FC1. R(x, y)
Правила для условного оператора
Для условного оператора if (C) A(x: y) else B(x: y) определим правила:
Правило FC1. R(x, y)

Правило FC2. R(x, y) & ¬C ├ LS(B(x: y))
Лемма 9. Если истинны правила FC1 и FC2, то истинна следующая формула:
R(x, y) ⇒ LS(if (C) A(x: y) else B(x: y))
Доказательство. Формула LS(if (C) A(x: y) else B(x: y)) эквивалентна
(C ⇒ LS(A(x: y))) & (¬C ⇒ LS(B(x: y)))
Таким образом, требуется доказать истинность:
R(x, y) ⇒ (C ⇒ LS(A(x: y))) & (¬C ⇒ LS(B(x: y)))
Последняя формула эквивалентна конъюнкции формул:
R(x, y) ⇒ (C ⇒ LS(A(x: y)))
R(x, y) ⇒ (¬C ⇒ LS(B(x: y)))
А эти формулы эвивалентны правилам FC1 и FC2. □
Слайд 28Правила для оператора суперпозиции
Для оператора суперпозиции A(x: z); B(x, z: y) определим правила: более общего
Правила для оператора суперпозиции
Для оператора суперпозиции A(x: z); B(x, z: y) определим правила: более общего

Правило FS1. R(x, y) ├ ∃z. LS(A(x: z))
Правило FS2. R(x, y) & LS(A(x: z)) ├ LS(B(x, z: y))
Лемма 3. Если истинны правила FS1 и FS2, то истинна следующая формула:
R(x, y) ⇒ LS(A(x: z); B(x, z: y))
Доказательство. Формула LS(A(x: z); B(x, z: y)) эквивалентна ∃z.(LS(A(x: z)) & LS(B(x, z: y))). Пусть истинно R(x, y). Докажем истинность ∃z.(LS(A(x: z)) & LS(B(x, z: y))). По правилу FS1 истинна формула ∃z. LS(A(x: z)). Допустим для некоторого z0 истинно LS(A(x: z0)). По правилу FS2 истинна формула LS(B(x, z0: y)). В итоге, будет истинна формула ∃z.(LS(A(x: z)) & LS(B(x, z: y))). □
• позиция квантора существования
• вхождение LS(…) в левой части
Слайд 29Правила для нерекурсивного вызова
Пусть имеется нерекурсивный вызов предиката A(x: y) со спецификацией:
{P(x)} A(x: y) {Q(x, y)} (3)
Для
Правила для нерекурсивного вызова
Пусть имеется нерекурсивный вызов предиката A(x: y) со спецификацией:
{P(x)} A(x: y) {Q(x, y)} (3)
Для

Правило FB1. R(x, y) ├ P(x) & Q(x, y)
Лемма 15. Допустим, нерекурсивный вызов предиката A(x: y) является корректным, а его спецификация (3) ⎯ однозначна. Если истинно правило FB1, то истинна следующая формула:
R(x, y) ⇒ LS(A(x: y))
Доказательство. Пусть истинно R(x, y). Докажем истинность LS(A(x: y)). Поскольку истинна правая часть правила FB1, то истинна формула P(x) & Q(x, y) в правой части. В соответствии с леммой 2.9 истинна формула P(x) & Q(x, y) ⇒ LS(A(x: y)) и, следовательно, LS(A(x: y)). □
Слайд 304. Система правил декомпозиции доказательства корректности операторов 4.4. Правила для общего случая
4. Система правил декомпозиции доказательства корректности операторов 4.4. Правила для общего случая

Слайд 31Декомпозиция для параллельного оператора
{P(x)} B(x: y) {Q(x, y)}
Corr(B, P, Q) ≅ P(x) ⇒ [LS(B(x, y))
Декомпозиция для параллельного оператора
{P(x)} B(x: y) {Q(x, y)}
Corr(B, P, Q) ≅ P(x) ⇒ [LS(B(x, y))

{P(x)} A(x: y) || B(x: z) {Q(x, y, z)}
Q(x, y, z) ≅ Q1(x, y) & Q2(x, z)
Лемма.
Corr(A(x: y) || B(x: z), P, Q) =
Corr(A(x: y), P, Q1) & Corr(B(x: z), P, Q2)
Слайд 32Декомпозиция для условного оператора
{P(x)} B(x: y) {Q(x, y)}
Corr(B, P, Q) ≅ P(x) ⇒ [LS(B(x, y))
Декомпозиция для условного оператора
{P(x)} B(x: y) {Q(x, y)}
Corr(B, P, Q) ≅ P(x) ⇒ [LS(B(x, y))

{P(x)} if (C) A(x: y) else B(x: y) {Q(x, y)}
Лемма.
Corr(if (C) A(x: y) else B(x: y), P, Q) =
Corr(A(x: y), P & C, Q) & Corr(B(x: y), P & ¬C, Q)
Слайд 33Декомпозиция для оператора суперпозиции
Рассмотрим спецификацию оператора суперпозиции в виде тройки Хоара:
{P(x)}
Декомпозиция для оператора суперпозиции
Рассмотрим спецификацию оператора суперпозиции в виде тройки Хоара:
{P(x)}

Предположим, что оператор A коррекетн. Спецификация представлены тройками:
{PA(x)} A {QA(x, z)},
Определим правила, гарантирующие корректность оператора суперпозиции (2.12).
Правило RS17. P(x) ├ PA(x) & ∀z (QA(x, z) ⇒ ∃y LS(B)(z, y)).
Правило RS18. P(x) & ∃z (QA(x, z) & LS(B)(z, y)) ├ Q(x, y).
Лемма 2.5. Пусть предусловие P(x) истинно. Допустим, оператор A корректен. Если правила RS1 и RS2 истинны, то оператор суперпозиции (2.12) является корректным.
Слайд 34Задачи верификации и синтеза
на примере оператора суперпозиции
A(x: y) ≡
Задачи верификации и синтеза
на примере оператора суперпозиции
A(x: y) ≡

Операторы B(x: z) и C(z: y) корректны относительно своих спецификаций [PB(x), QB(x, z)] и [PC(z), QC(z, y)].
Спецификация [P(x), Q(x, y)] тотальна. Корректность предиката A гарантируется в случае истинности правил:
Правило LS1. P(x) ├ PB(x)
Правило LS2. P(x) & Q(x, y) & QB(x, z) ├ PC(z) & QC(z, y)
Задача дедуктивной верификации
Задача программного синтеза: требуется построить программу предиката A, представленного тотальной спецификацией [P(x), Q(x, y)].
Пусть для некоторых предикатов PB(x), QB(x, z), PC(z) и QC(z, y) доказана истинность правил LS1 и LS2. Тогда синтезируем программу (3).
Корректность оператора S(x: y) относительно однозначной и тотальной спецификации [P(x), Q(x, y)]:
P(x) & Q(x, y) ⇒ LS(S(x: y)) (2)
Слайд 355. Построение языка предикатного программирования.
Методы доказательства корректности предикатных программ
5. Построение языка предикатного программирования.
Методы доказательства корректности предикатных программ

Слайд 36P(x) ⇒ [ LS(S)(x, y) ⇒ Q(x, y) ] & ∃y. LS(S)(x, y) (4.1)
P(x)
P(x) ⇒ [ LS(S)(x, y) ⇒ Q(x, y) ] & ∃y. LS(S)(x, y) (4.1)
P(x)
![P(x) ⇒ [ LS(S)(x, y) ⇒ Q(x, y) ] & ∃y. LS(S)(x,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/432424/slide-35.jpg)
Система правил доказательства корректности оператора суперпозиции, параллельного оператора и условного оператора
Исчисление вычислимых предикатов ― множество вычислимых формул языка исчисления предикатов ― язык CCP (Calculus of Computable Predicates)
минимальный полный базис языка предикатного программирования
Язык предикатного программирования P (Predicate programming language).
Расширяющаяся последовательность языков:
CCP = P0, P1, P2, P3, P4 = P.
Слайд 37 Язык P1: подстановка определения предиката на место вызова
Подстановка определения предиката
Язык P1: подстановка определения предиката на место вызова
Подстановка определения предиката

LS({ K(t: z) }) ≅ LS(K(t: z)) (5.1)
runBlock(s, { K(t: z) }):
runStat(s, K(t: z)) (5.2)
Программа П’, получаемая из программы П подстановкой определения предиката на место вызова, эквивалентна программе П’: исполнение любого предиката программы П’ на фиксированном наборе аргументов дает тот же результат, что и в программе П.
Язык P1: многократное произвольное применение подстановок определений предикатов на место вызовов.
Конструкция: вызов или блок как подоператор в трех базисных операторах
Слайд 38Язык P2: оператор суперпозиции и параллельный оператор общего вида
Операторы { A(…); B(…) }; C(…) и
Язык P2: оператор суперпозиции и параллельный оператор общего вида
Операторы { A(…); B(…) }; C(…) и

Эквивалентны { A(…) || B(…) } || C(…) и A(…) || { B(…) || C(…) }
Язык P2: оператор суперпозиции и параллельный оператор общего вида: A1(…); A2(…); … ; An(…) и A1(…) || A2(…) || … || An(…) для n > 1.
P(x){B1(x: z1); B2(z1: z2);...; Bj(zj-1: zj);...; Bn(zn-1: y)}Q(x, y) (5.3)
x, z1, z2, …, zn-1, y ⎯ различные непересекающиеся наборы переменных, B1, B2, …, Bn обозначают предикаты или блоки языка P1 со спецификациями (предусловиями и постусловиями) PB1(x), QB1(x, z1), PB2(z1), QB2(z1, z2), …, PBn(zn-1), QBn(zn-1, y).
Слайд 39LS(B1(x: z1); B2(z1: z2);...; Bj(zj-1: zj);...; Bn(zn-1: y)) ≡
∃ z1, z2, …, zn-1.LS(B1(x: z1)) & LS(B2(z1: z2)) &...&
& LS(Bj(zj-1: zj)) &...& LS(Bn(zn-1: y)) (5.4)
runStat(s, B1(x: z1); …; Bn(zn-1: y))
runCallBlock(s, B1(x: z1));
LS(B1(x: z1); B2(z1: z2);...; Bj(zj-1: zj);...; Bn(zn-1: y)) ≡
∃ z1, z2, …, zn-1.LS(B1(x: z1)) & LS(B2(z1: z2)) &...&
& LS(Bj(zj-1: zj)) &...& LS(Bn(zn-1: y)) (5.4)
runStat(s, B1(x: z1); …; Bn(zn-1: y))
runCallBlock(s, B1(x: z1));

runCallBlock(s, B2(z1: z2)); .....;
runCallBlock(s, Bj(zj-1: zj)); .....;
runCallBlock(s, Bn(zn-1: y))
Слайд 40Параллельный оператор общего вида
P(x){B1(x: y1) || B2(x: y2)||...||Bj(x: yj)||...||Bn(x: yn)}Q(x, y) (5.7)
x, y = y1,…,yn ⎯ различные
Параллельный оператор общего вида
P(x){B1(x: y1) || B2(x: y2)||...||Bj(x: yj)||...||Bn(x: yn)}Q(x, y) (5.7)
x, y = y1,…,yn ⎯ различные

LS(B1(x: y1) || B2(x: y2) ||...|| Bj(x: yj) ||...|| Bn(x: yn)) ≡
LS(B1(x: y1)) & LS(B2(x: y2)) & ... &
& LS(Bj(x: yj)) & ... & LS(Bn(x: yn)) (5.8)
runStat(s, B1(…) || B2(…) || … || Bn(…))
runCallBlock(s, B1(x: y1)) || (5.9)
runCallBlock(s, B2(x: y2)) || ... ||
runCallBlock(s, Bj(x: yj)) || ... ||
runCallBlock(s, Bn(x: yn))
Слайд 41Правило опускания скобок:
{A(…); B(…)} || C(…) → A(…); B(…) || C(…).
A(x: y); {B(z: t) || C(u: v)}
Набор y пересекается с набором z
Правило опускания скобок:
{A(…); B(…)} || C(…) → A(…); B(…) || C(…).
A(x: y); {B(z: t) || C(u: v)}
Набор y пересекается с набором z

A(x: y); {B(z: t) || C(u: v)} ≡ {A(x: y); B(z: t)} || C(u: v) ≡
≡ A(x: y); B(z: t) || C(u: v).
{A(x: y) || B(z: t)}; C(u: v) ≡ A(x: y) || B(z: t); C(u: v),
если наборы y и u не пересекаются.
Слайд 42Язык P2: другое обобщение оператора суперпозиции
B(x: z); C(x, z: y) ⎯ обобщение оператора суперпозиции.
P(x) {B1(x: z1); B2(x, z1: z2);...;
Язык P2: другое обобщение оператора суперпозиции
B(x: z); C(x, z: y) ⎯ обобщение оператора суперпозиции.
P(x) {B1(x: z1); B2(x, z1: z2);...;

(5.10)
Частный случай: B(x: z); C(u, z: y), набор u ⎯ часть набора x
Наиболее общая форма суперпозиции:
A(x: t, y) ≡ P(x) {B(x: z, t); C(x, z: y)} Q(x, t, y) (5.11)
наборы x и t могут быть пустыми
Спецификации: PB(x), QB(x, z, t), PC(x, z), QC(x, z, y).
Слайд 43B1(x: x1, z, t1) ≡ PB(x) {B(x: z, t1) || x1 = x} QB(x, z, t1)
B1(x: x1, z, t1) ≡ PB(x) {B(x: z, t1) || x1 = x} QB(x, z, t1)

C1(x1,z,t1: y, t) ≡ PC(x1, z) {C(x1, z: y) || t = t1} QC(x1,z,y) & t = t1
Поскольку B1(x: x1, z, t1); C1(x1, z, t1: t, y) ≡ B(x: z, t); C(x, z: y), то справедливо другое определение предиката A:
A(x: t, y) ≡ P(x) {B1(x: x1, z, t1); C1(x1, z, t1: t, y)} Q(x, t, y) (5.12)
LS(B(x: z, t); C(x, z: y)) ≡ ∃z. (LS(B(x: z, t)) & LS(C(z, y))) (5.13)
runCallBlock(s, B(x: z, t)); (5.14)
runCallBlock (s, C(x, z: y))
Правило RS1’. P(x) ├
PB(x) & ∀x1, z, t1 ((QB(x, z, t1) & x1 = x) ⇒ PC(x1, z))
Правило RS2’. P(x) &
∃x1,z,t1 (QB(x1, z, t1) & x1 = x & QC(x1, z, y) & t = t1) ├
Q(x, t, y)
A(x: t, y) ≡ P(x) {B(x: z, t); C(x, z: y)} Q(x, t, y) (5.11)
Слайд 44Правило RS5. P(x) ├ PB(x) & ∀z, t (QB(x, z, t) ⇒ PC(x, z))
Правило
Правило RS5. P(x) ├ PB(x) & ∀z, t (QB(x, z, t) ⇒ PC(x, z))
Правило

Лемма 5.5. Пусть предусловие P(x) истинно. Допустим, операторы B и C корректны. Если правила RS5 и RS6 истинны, то оператор суперпозиции (5.11) является корректным.
Правило LS1’. P(x) ├ PB(x)
Правило LS2’. P(x) & Q(x, t, y) & QB(x, z, t1) & x1=x ├
PC(x1, z) & QC(x1, z, y) & t = t1
Правило LS6. P(x) ├ PB(x)
Правило LS7. P(x) & Q(x, t, y) & QB(x, z, t1) ├
PC(x, z) & QC(x, z, y) & t = t1
Лемма 5.6. Допустим, спецификация оператора суперпозиции (5.11) реализуема, операторы B и C однозначны в области предусловий и корректны, а их спецификации ⎯ однозначны. Если правила LS6 и LS7 истинны, то оператор суперпозиции (5.11) является корректным.
Слайд 45Язык P3: выражения
Функциональная форма. Предикат A(t: z).
z = A(t) ≅ A(t: z)
|z| = A(t), если
Язык P3: выражения
Функциональная форма. Предикат A(t: z).
z = A(t) ≅ A(t: z)
|z| = A(t), если

Инфиксная и постфиксная нотация как разновидность функциональной формы
+(x, y: z), -(x, y: z), -(x: y), <(x, y: b)
z = x + y, z = x - y, y = -x , b = x < y.
Изображения констант:
ConsIntZero( : x) ConsIntOne( : x) valInt(“2089” : x)
x = 0 x = 1 x = 2089
B(x: z); C(x, z: y) ≡ z =B(x); C(x, z: y) ≡ C(x, B(x): y)
{ A(x: y) || B(z: t) }; C(y, t: u) ≡
≡ { y = A(x) || t = B(z) }; C(y, t: u) ≡ C(A(x), B(z): u)
Слайд 46D(x, z: u) ≡ P(x, z) {C(A(x), B(z): u)} Q(x, z, u) (5.15)
E(x, z: y,
D(x, z: u) ≡ P(x, z) {C(A(x), B(z): u)} Q(x, z, u) (5.15)
E(x, z: y,

D(x, z: u) ≡ P(x, z) { E(x, z: y, t); C(y, t: u)} Q(x, z, u) (5.16)
Правило RS1’.
P(x, z) ├ PA(x) & PB(z) & ∀y,t (QA(x, y)& QB(z, t) ⇒ PC(y, t))
Правило RS2’.
P(x, z) & ∃y,t. (QA(x, y) & QB(z, t) & QC(y, t, u)) ├ Q(x, z, u)
Слайд 47Правило RS7. P(x, z) ├ PA(x) & PB(z) & PC(A(x), B(z))
Правило RS8.
Правило RS7. P(x, z) ├ PA(x) & PB(z) & PC(A(x), B(z))
Правило RS8.

Лемма 5.7. Пусть предусловие P(x, z) истинно. Допустим, операторы A, B и C корректны, операторы A и B, а также их спецификации PA(x), QA(x, y), PB(z), QB(z, t) ⎯ однозначны.. Если правила RS7 и RS8 истинны, то оператор (5.15) со спецификацией P(x, z) и Q(x, z, u) является корректным.
Для получения правил серии L применим правила LS1 и LS2 для оператора в правой части (5.16).
Правило LS1’. P(x, z) ├ PA(x) & PB(z).
Правило LS2’.
P(x, z) & Q(x, z, u) & QA(x, y) & QB(z, t)├ PC(y, t) & QC(y, t, u).
Слайд 48Правило LS8. P(x, z) ├ PA(x) & PB(z).
Правило LS9.
P(x, z)
Правило LS8. P(x, z) ├ PA(x) & PB(z).
Правило LS9.
P(x, z)

Лемма 5.8. Допустим, спецификация P(x, z) и Q(x, z, u) оператора (5.15) реализуема, операторы A, B и C однозначны в области предусловий и корректны, а их спецификации ⎯ однозначны. Если правила LS8 и LS9 истинны, то оператор (5.15) является корректным.
Понятие выражения.
z = a * b; y = z + c ≡ y = (a * b) + c ≡ y = a * b + c
Правила приоритетов операций
Переменные, изображения констант, вызовы функций и их представление в виде операций являются частными случаями понятия выражения.
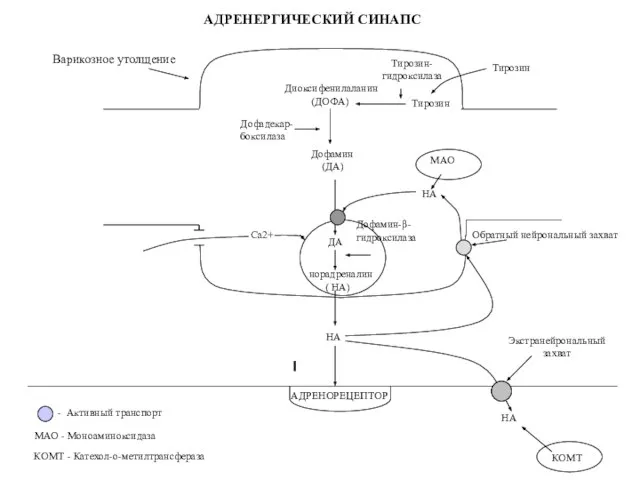 Адреномиметики
Адреномиметики Sport in Canada
Sport in Canada АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов
АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов Презентация на тему Русский герой сказок: Иван-дурак
Презентация на тему Русский герой сказок: Иван-дурак  Путешествие на водопад Атыш
Путешествие на водопад Атыш Помада Creamy Glam
Помада Creamy Glam Презентация по английскому Королевская семья Великобритании
Презентация по английскому Королевская семья Великобритании tema-gribi-rodnaya-tropinka_ru
tema-gribi-rodnaya-tropinka_ru Работа социального педагога с детьми имеющих отклоняющее поведение.
Работа социального педагога с детьми имеющих отклоняющее поведение. Комплекс упражнений утренней гимнастики
Комплекс упражнений утренней гимнастики Службы для электронного общения
Службы для электронного общения Характер и темперамент
Характер и темперамент Обществознание
Обществознание Материально-техническая база одно из условий эффективной реализации профильного обучения.
Материально-техническая база одно из условий эффективной реализации профильного обучения. Способ тепловой обработки сыпучих материалов и устройства для его осуществления
Способ тепловой обработки сыпучих материалов и устройства для его осуществления Архитектура Санкт-Петербурга
Архитектура Санкт-Петербурга project
project Greenway. Жизнь без химии с заботой о семье и природе
Greenway. Жизнь без химии с заботой о семье и природе Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16
Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16 Сказочные птицы
Сказочные птицы Леонардо Да Винчи
Леонардо Да Винчи Как преодолеть стресс перед экзаменом
Как преодолеть стресс перед экзаменом Признаки нарушения адаптации в почерке
Признаки нарушения адаптации в почерке Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017
Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017 Доходы предприятия и финансовые результаты его деятельности
Доходы предприятия и финансовые результаты его деятельности Алтайский государственный университет
Алтайский государственный университет Методика оформление. Пушкинская карта
Методика оформление. Пушкинская карта Презентация на тему Социальная информатика
Презентация на тему Социальная информатика