Содержание
- 2. Краткая аннотация курса лекций Электронный курс лекций (ЭКЛ) по разделу «Инженерная графика» является комплектом лекций по
- 3. Содержание 1. Конструктивное отображение пространства. 1.1 Комплексный чертеж (эпюр Монжа), как система плоских эквивалентов пространства. 1.2
- 4. Инженерная графика Лекция №1 «Конструктивное отображение пространства» Автор: Посягина Т.А.
- 5. Теоретические основания начертательной геометрии связаны с именем Г. Монжа (1746-1818) 1.1 Комплексный чертеж (эпюр Монжа), как
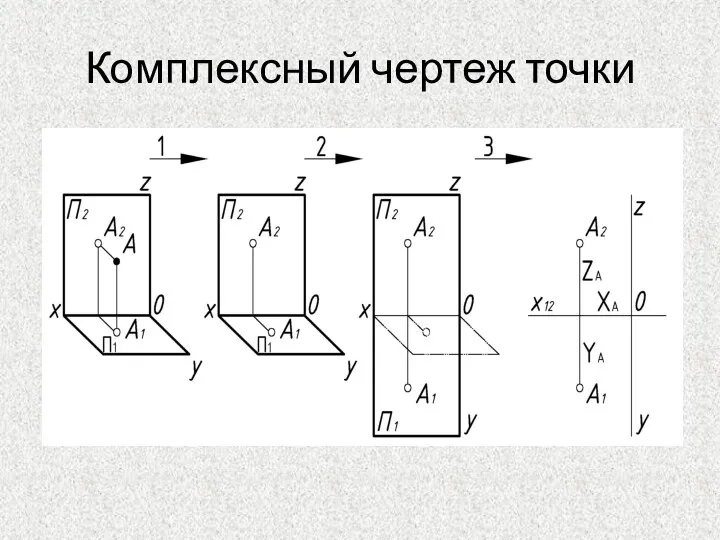
- 7. Комплексный чертеж точки
- 8. Комплексный чертеж фронтально проецирующей прямой
- 9. Комплексный чертеж горизонтально проецирующей прямой
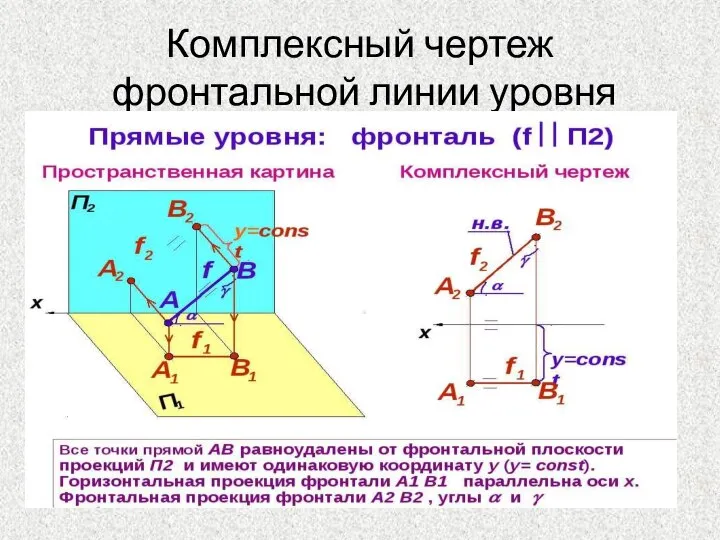
- 10. Комплексный чертеж фронтальной линии уровня
- 11. Комплексный чертеж прямой общего положения
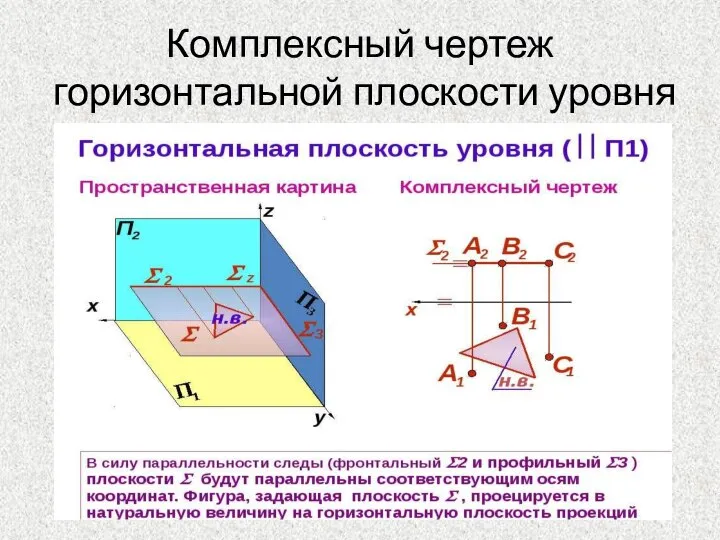
- 12. Комплексный чертеж горизонтальной плоскости уровня
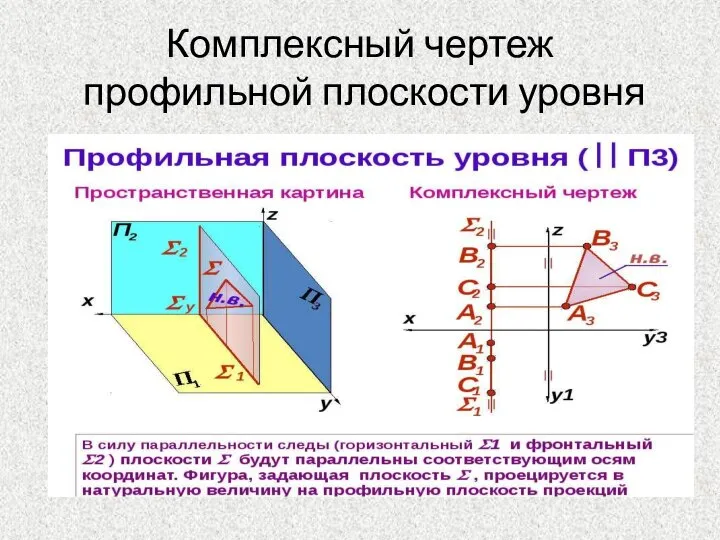
- 13. Комплексный чертеж профильной плоскости уровня
- 14. Комплексный чертеж фронтально проецирующей прямой
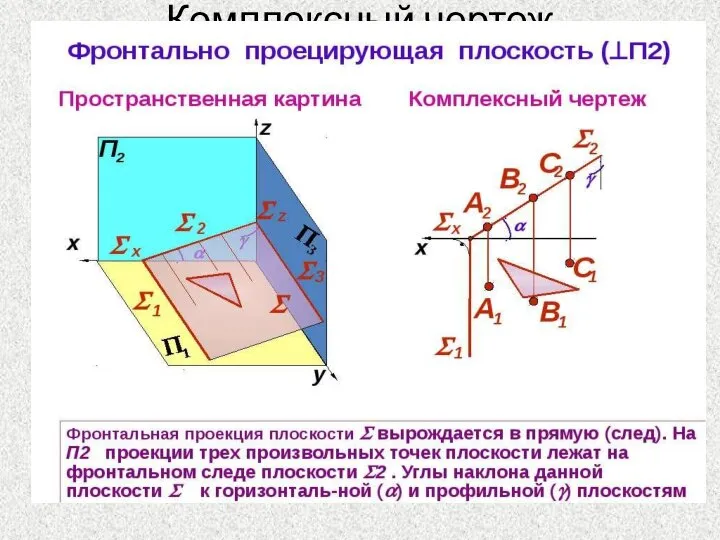
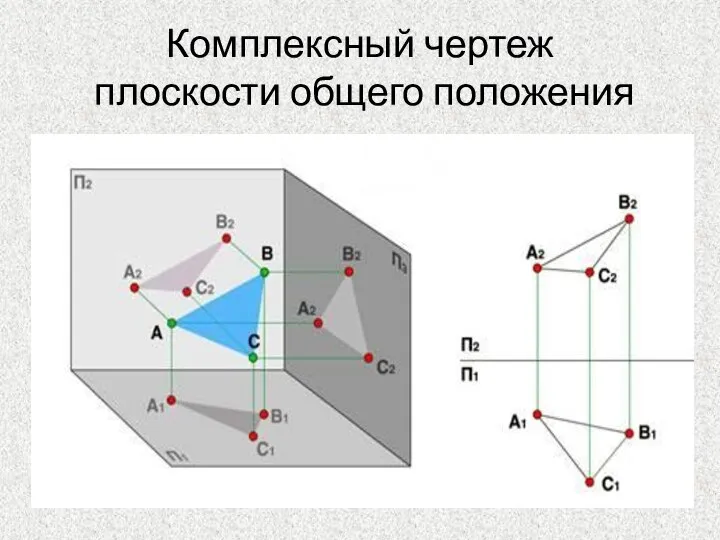
- 15. Комплексный чертеж плоскости общего положения
- 16. 1.2 . Взаимное расположение прямых. Моделирование плоскости на комплексном чертеже. Взаимное расположение плоскостей в пространстве.
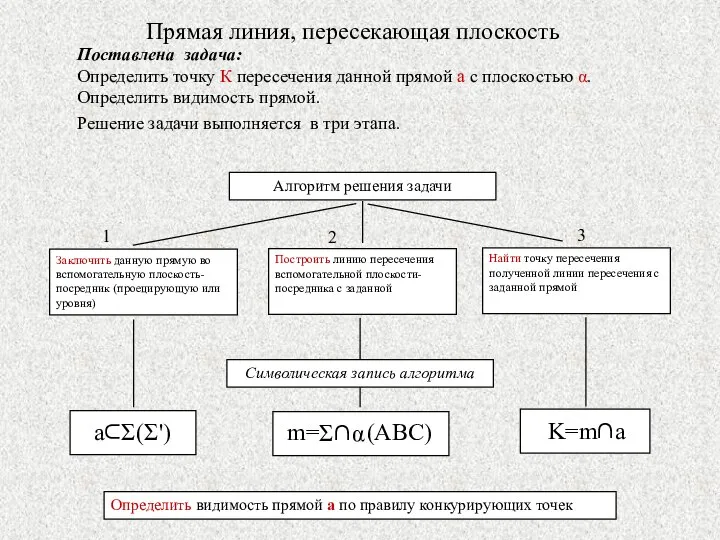
- 17. Прямая линия, пересекающая плоскость Поставлена задача: Определить точку К пересечения данной прямой а с плоскостью α.
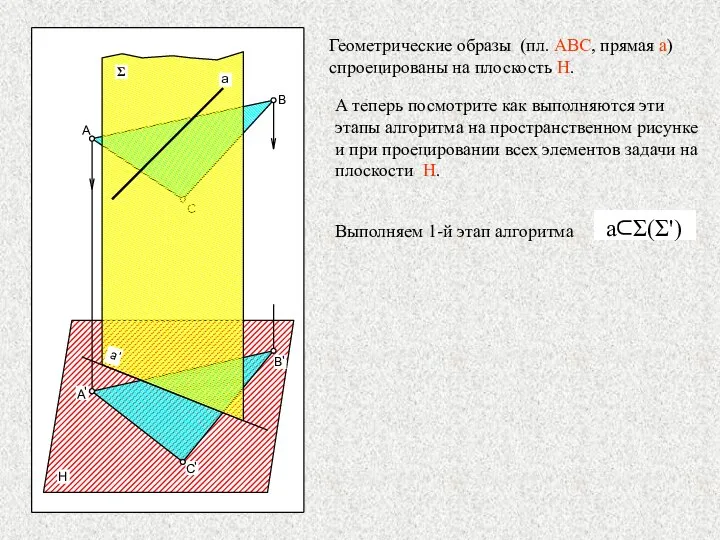
- 18. А теперь посмотрите как выполняются эти этапы алгоритма на пространственном рисунке и при проецировании всех элементов
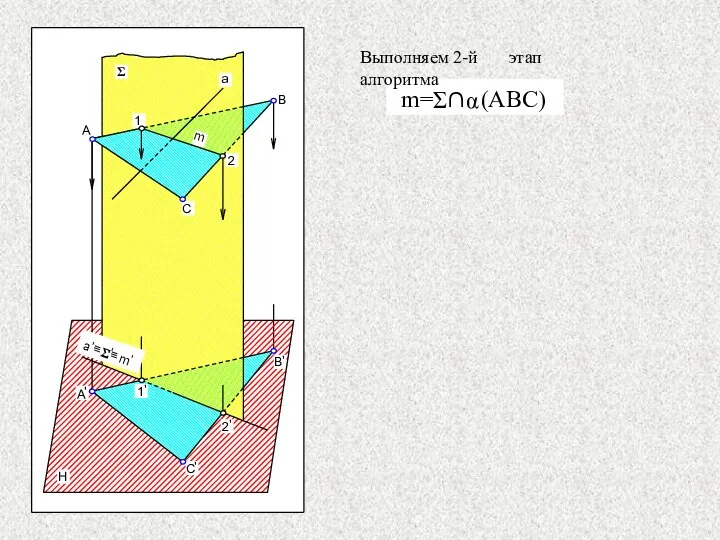
- 19. Выполняем 2-й этап алгоритма
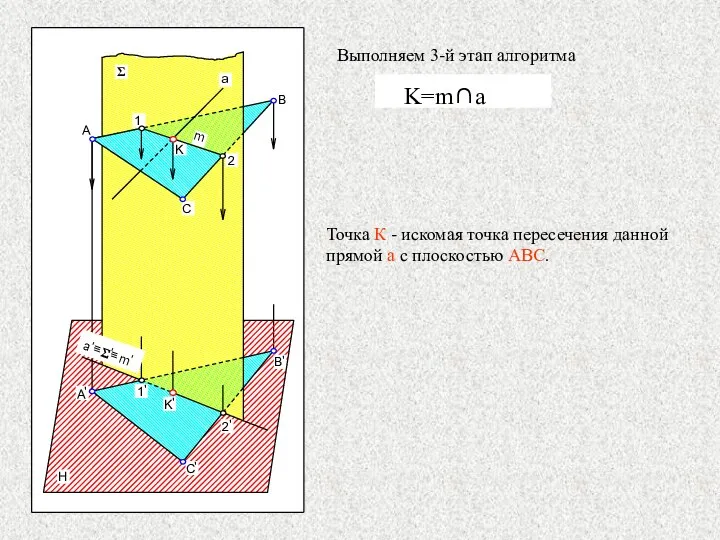
- 20. Точка К - искомая точка пересечения данной прямой а с плоскостью АВС. Выполняем 3-й этап алгоритма
- 21. Рассмотрим применение данного алгоритма при решении задачи на построение точки К пересечения прямой а с плоскостью
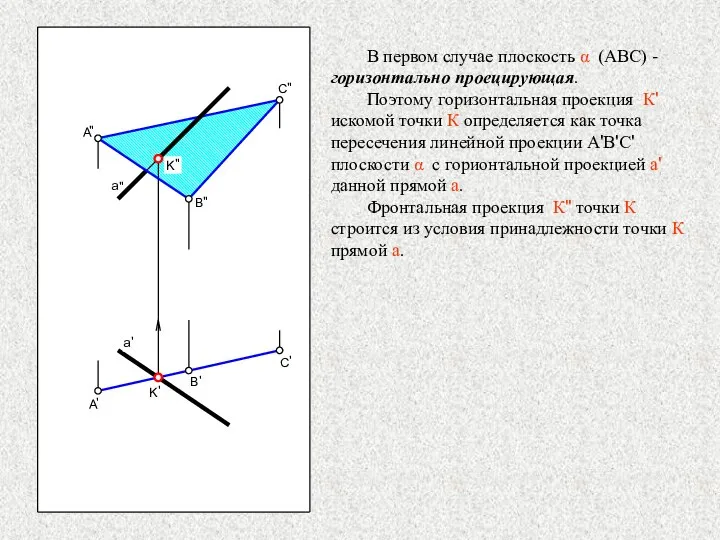
- 22. В первом случае плоскость α (АВС) - горизонтально проецирующая. Поэтому горизонтальная проекция К' искомой точки К
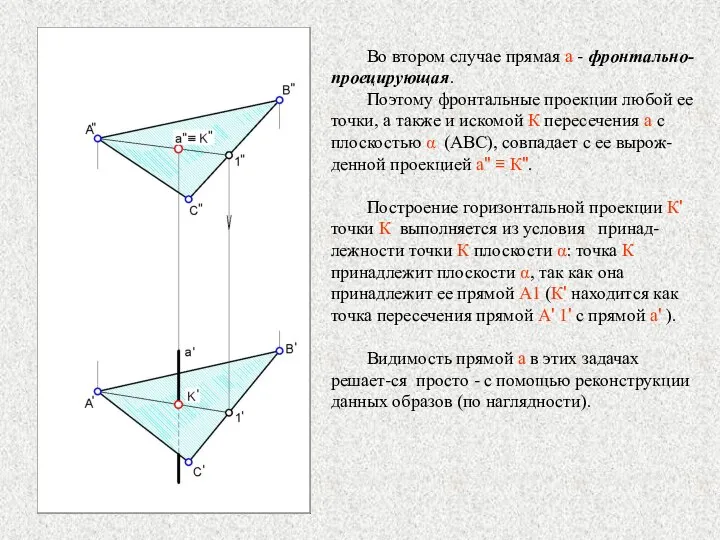
- 23. Во втором случае прямая а - фронтально-проецирующая. Поэтому фронтальные проекции любой ее точки, а также и
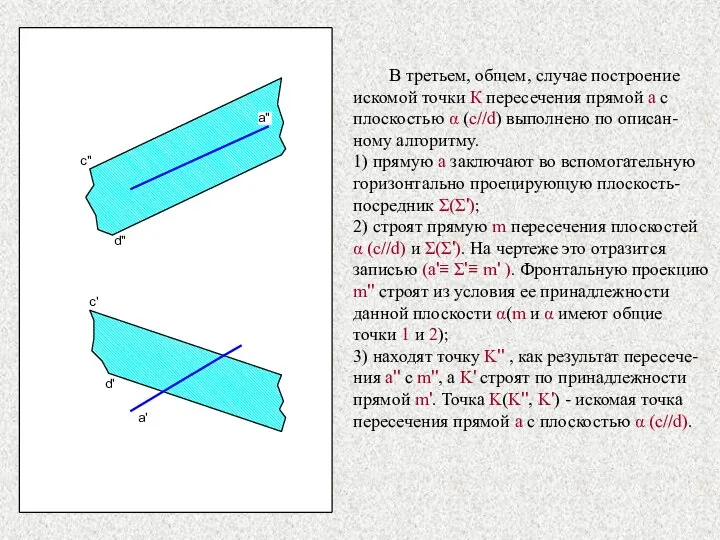
- 24. c" c' d" d' a' В третьем, общем, случае построение искомой точки К пересечения прямой а
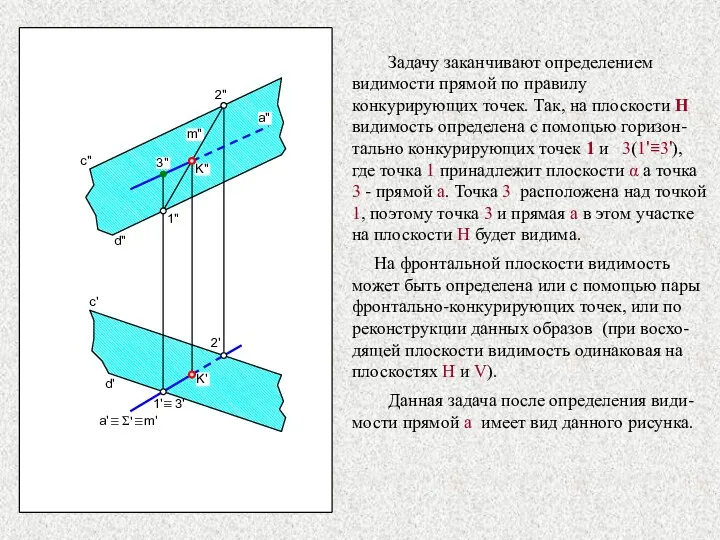
- 25. c" c' d" d' 1" 2" 2' Задачу заканчивают определением видимости прямой по правилу конкурирующих точек.
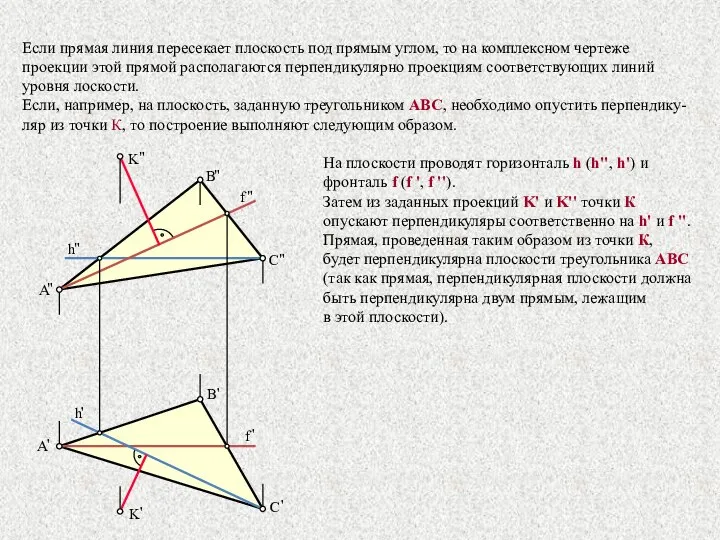
- 26. Если прямая линия пересекает плоскость под прямым углом, то на комплексном чертеже проекции этой прямой располагаются
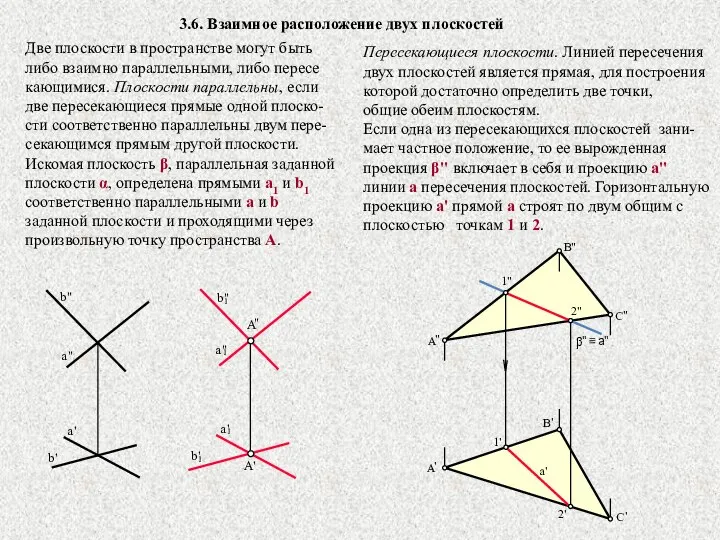
- 27. 3.6. Взаимное расположение двух плоскостей Две плоскости в пространстве могут быть либо взаимно параллельными, либо пересе
- 28. Определение линии пересечения двух плоскостей общего положения Для определения точек линии пересечения обе заданные плоскости α
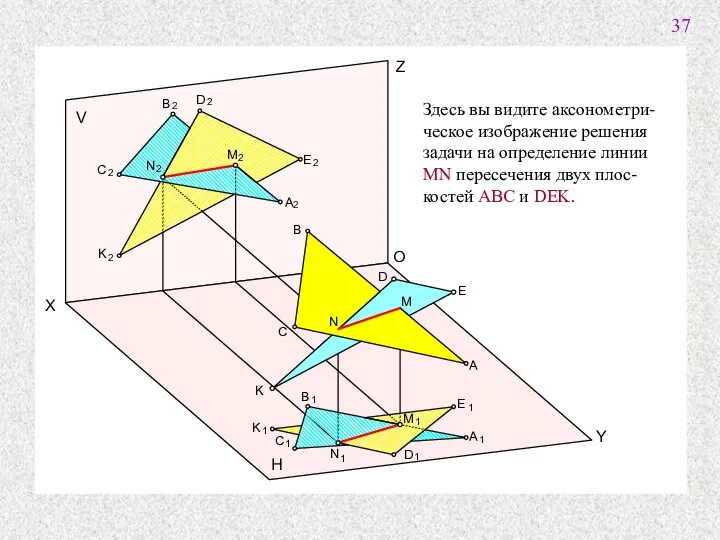
- 29. Y X Z V H A B C D E K M N O Здесь вы
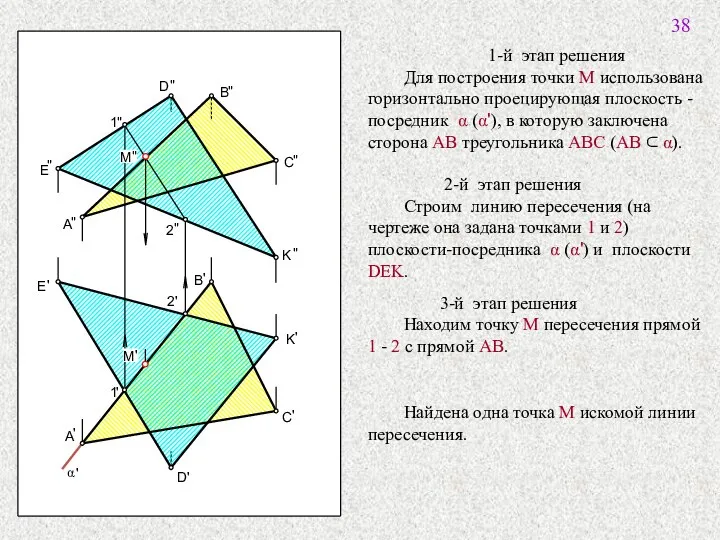
- 30. D " " E A " 1-й этап решения Для построения точки M использована горизонтально проецирующая
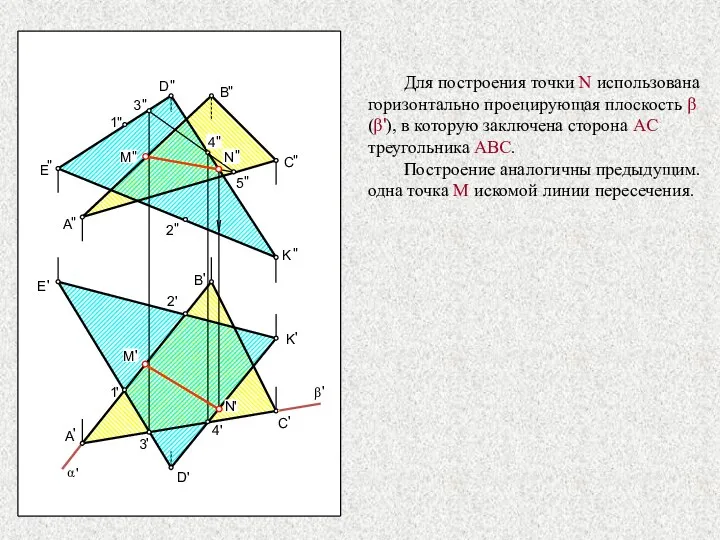
- 31. D " " E A " Для построения точки N использована горизонтально проецирующая плоскость β (β'),
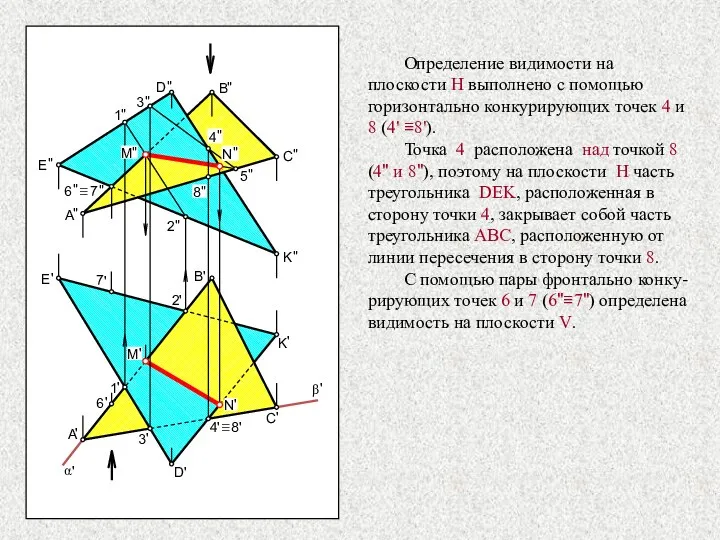
- 32. Определение видимости на плоскости H выполнено с помощью горизонтально конкурирующих точек 4 и 8 (4' ≡8').
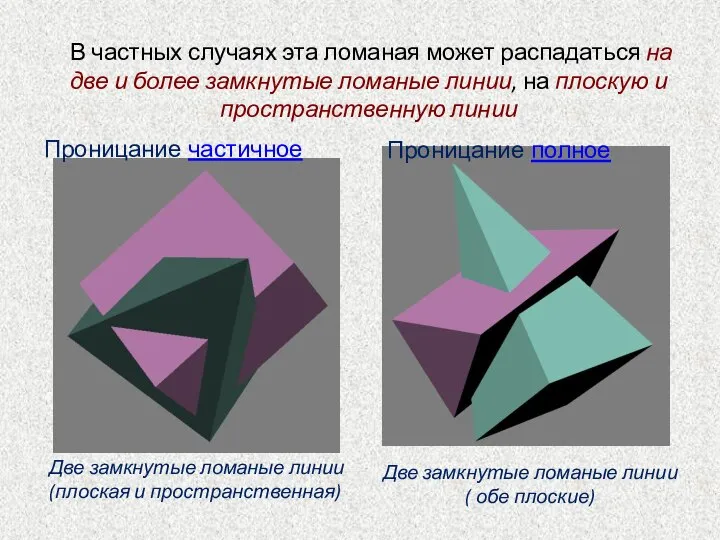
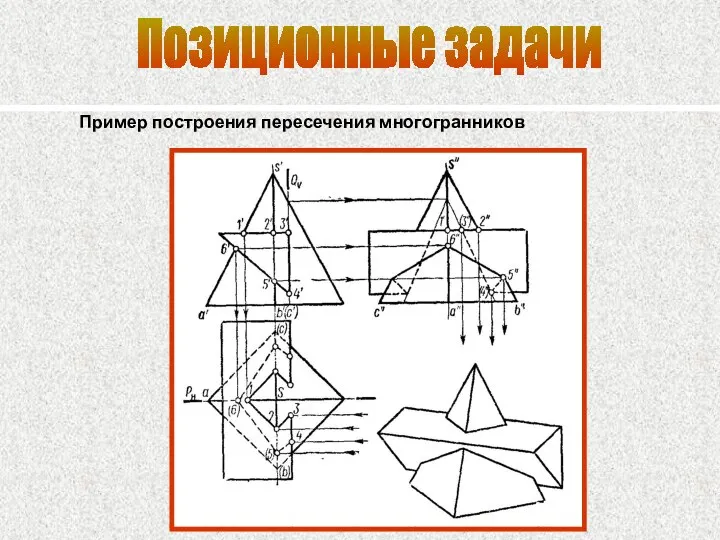
- 33. Две многогранные поверхности в общем случае пересекаются по пространственной замкнутой ломаной линии Проницание частичное
- 34. В частных случаях эта ломаная может распадаться на две и более замкнутые ломаные линии, на плоскую
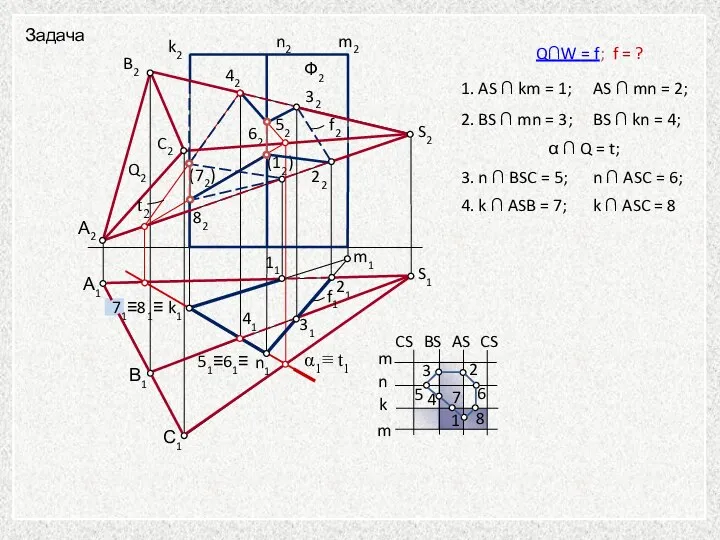
- 35. Способ ребер − построение вершин ломаной как точек пересечения ребер первого многогранника с гранями второго и
- 36. А1 В1 С1 S1 k1 m1 m2 n2 k2 S2 А2 B2 C2 41 31 21
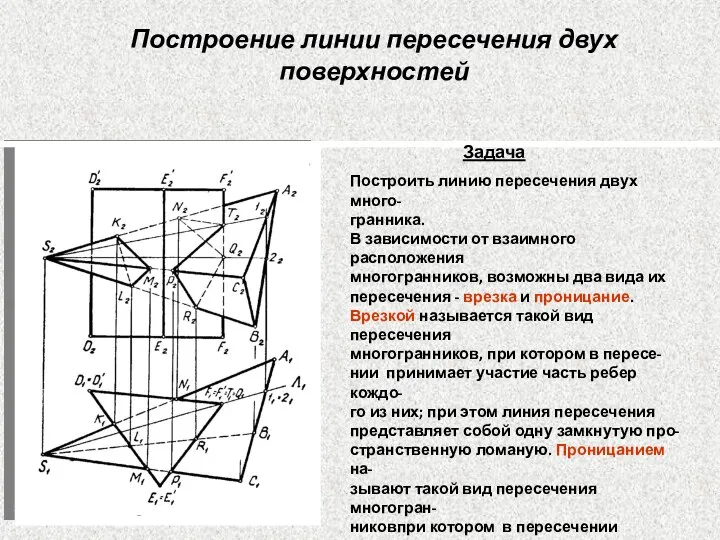
- 37. Построение линии пересечения двух поверхностей Задача Построить линию пересечения двух много- гранника. В зависимости от взаимного
- 38. Инженерная графика Лекция №2 «Преобразование ортогональных проекций. 2.1 Введение новых плоскостей проекций. 2.2 Применение способов преобразования
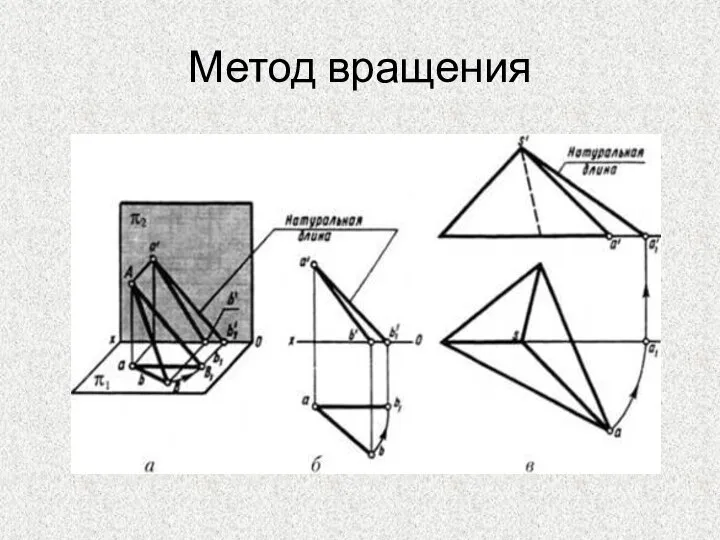
- 39. Метод вращения
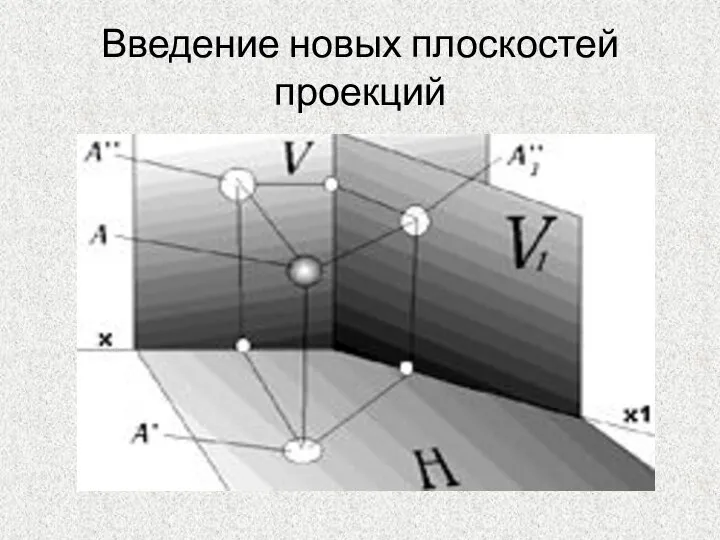
- 41. Введение новых плоскостей проекций
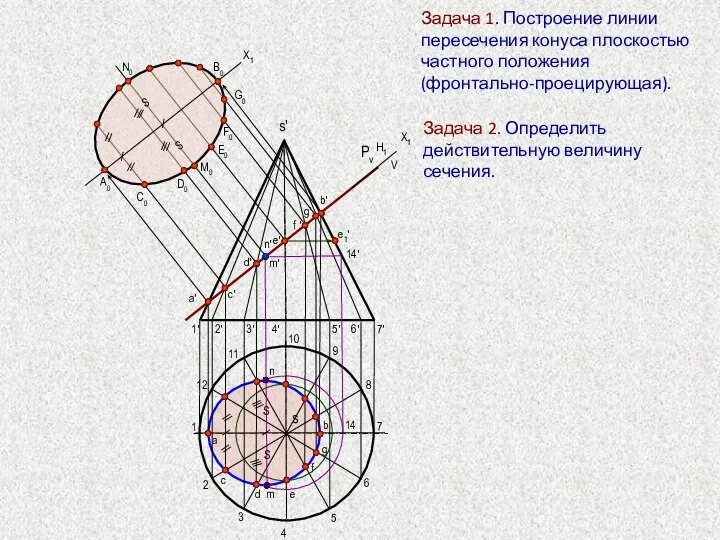
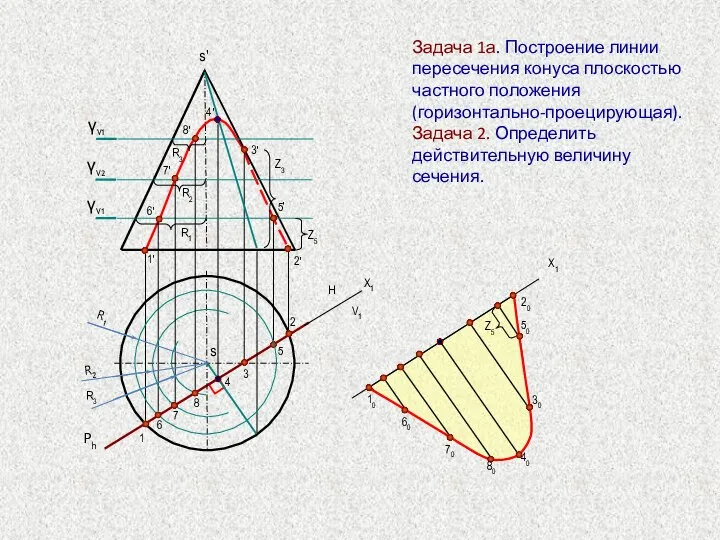
- 43. a' Задача 1. Построение линии пересечения конуса плоскостью частного положения (фронтально-проецирующая). 1 2 3 4 5
- 44. 1 1' s Ph 2 2' 3 3' 4 4' 5 5' γV1 R1 6 6'
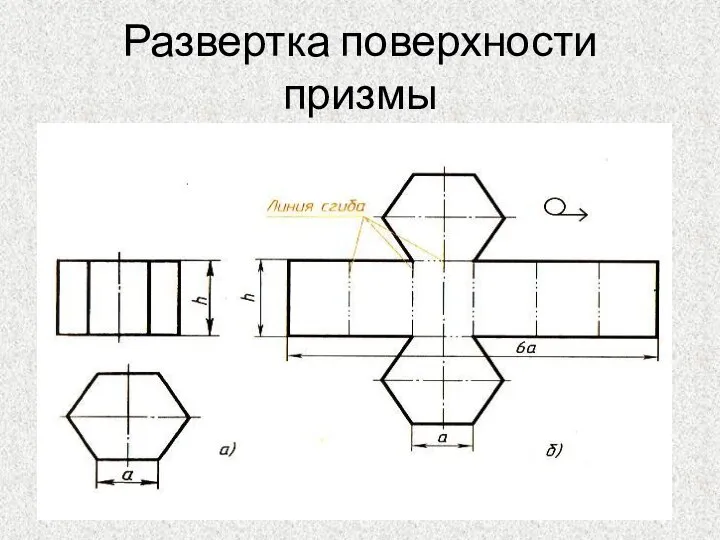
- 45. Развертка поверхности призмы
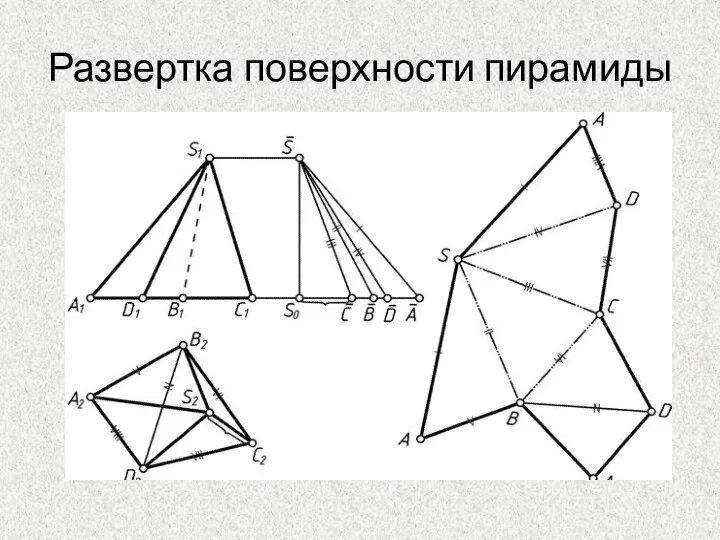
- 46. Развертка поверхности пирамиды
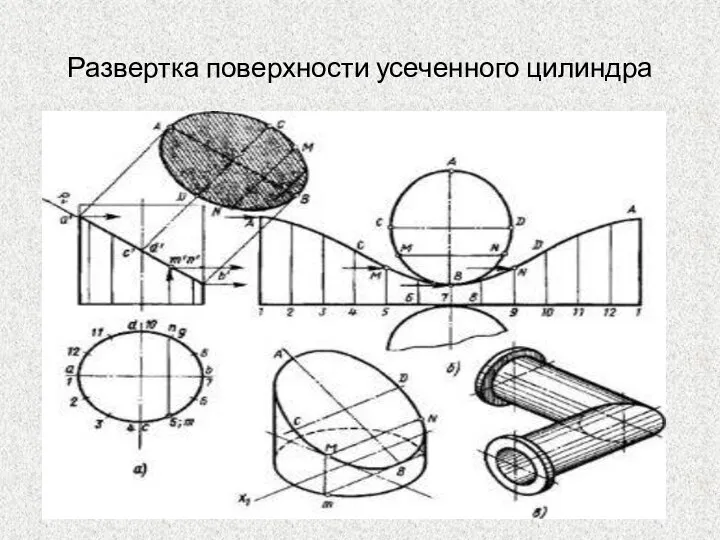
- 47. Развертка поверхности усеченного цилиндра
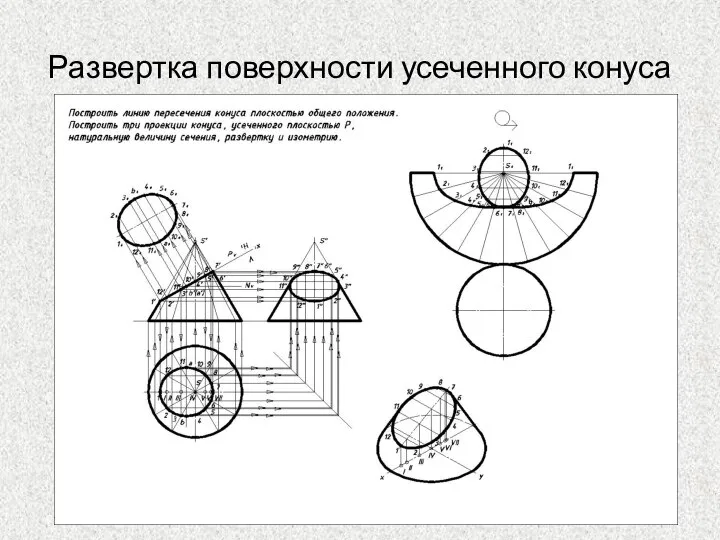
- 48. Развертка поверхности усеченного конуса
- 49. Инженерная графика Лекция №3 « Поверхности. Способ вспомогательных секущих плоскостей 1.1 Многогранники. Пересечение многогранников плоскостью и
- 50. Пересечение поверхностей. Способ вспомогательных секущих плоскостей.
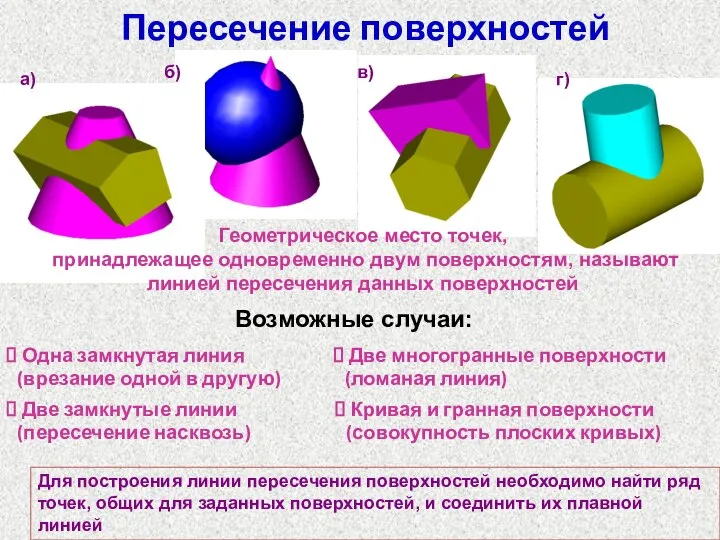
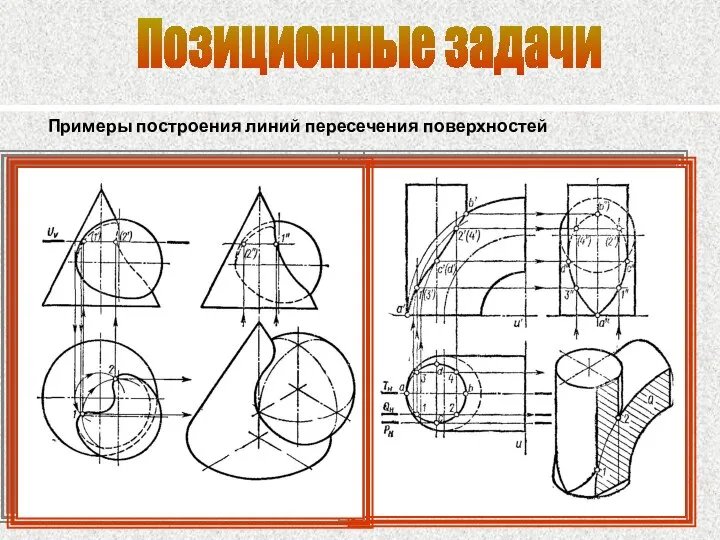
- 51. Пересечение поверхностей Для построения линии пересечения поверхностей необходимо найти ряд точек, общих для заданных поверхностей, и
- 52. Анализ заданных поверхностей Линия пересечения 2-х поверхностей в общем случае представляет собой пространственную кривую Если заданы
- 53. Анализ заданных поверхностей 4. Если одна из заданных поверхностей является проецирующей (цилиндр, призма),то одна из проекций
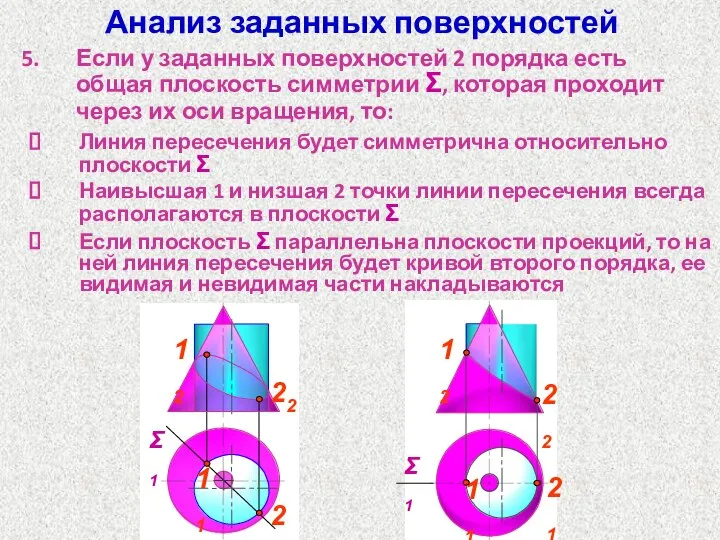
- 54. Анализ заданных поверхностей Если у заданных поверхностей 2 порядка есть общая плоскость симметрии Σ, которая проходит
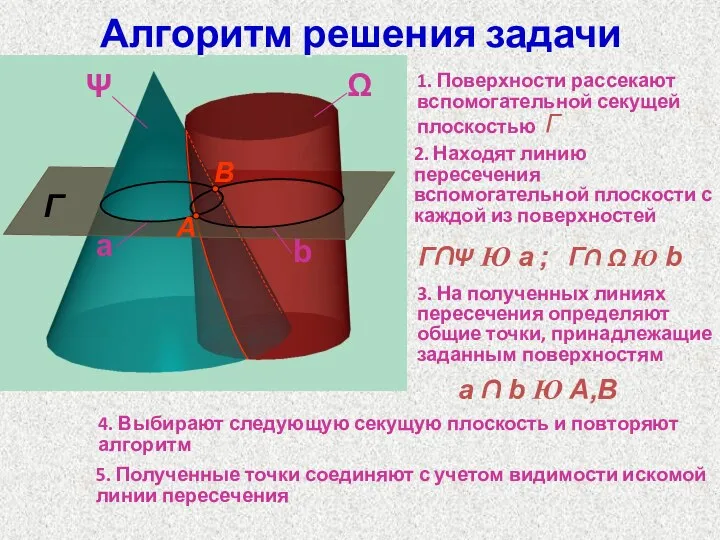
- 55. Алгоритм решения задачи Г 1. Поверхности рассекают вспомогательной секущей плоскостью Г 2. Находят линию пересечения вспомогательной
- 56. Методические указания Вспомогательные плоскости следует выбирать так, чтобы в сечении получались простые линии Сначала определяют опорные
- 57. Пересекающиеся поверхности (сфера и конус) имеют общую плоскость симметрии Ф(Ф1), являющейся фронтальной плоскостью уровня. Следовательно, фронтальные
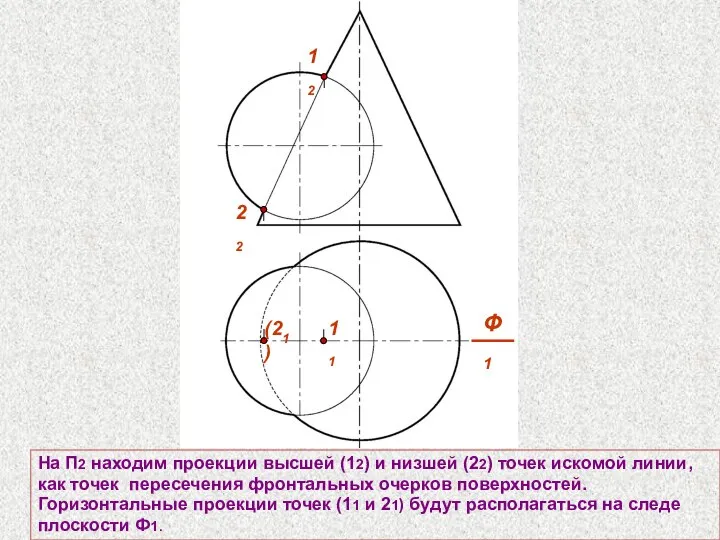
- 58. На П2 находим проекции высшей (12) и низшей (22) точек искомой линии, как точек пересечения фронтальных
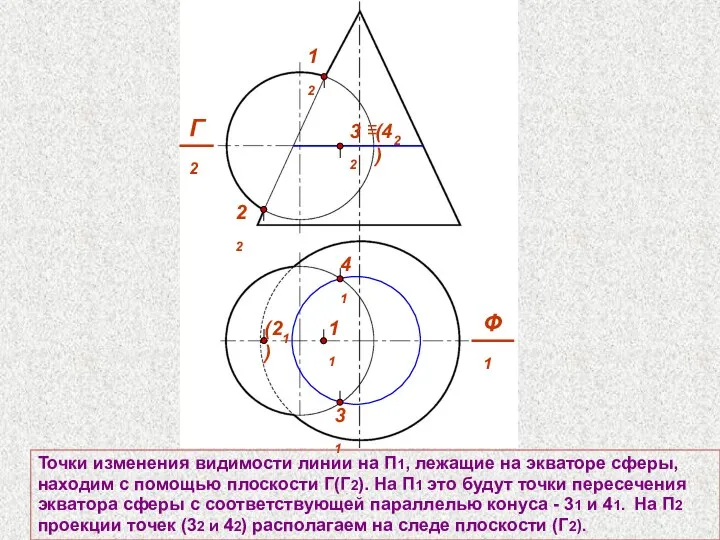
- 59. Точки изменения видимости линии на П1, лежащие на экваторе сферы, находим с помощью плоскости Г(Г2). На
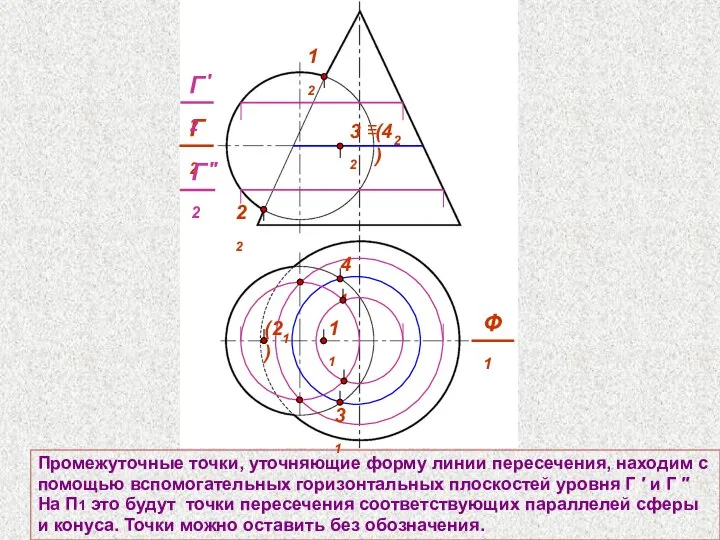
- 60. Промежуточные точки, уточняющие форму линии пересечения, находим с помощью вспомогательных горизонтальных плоскостей уровня Г ′ и
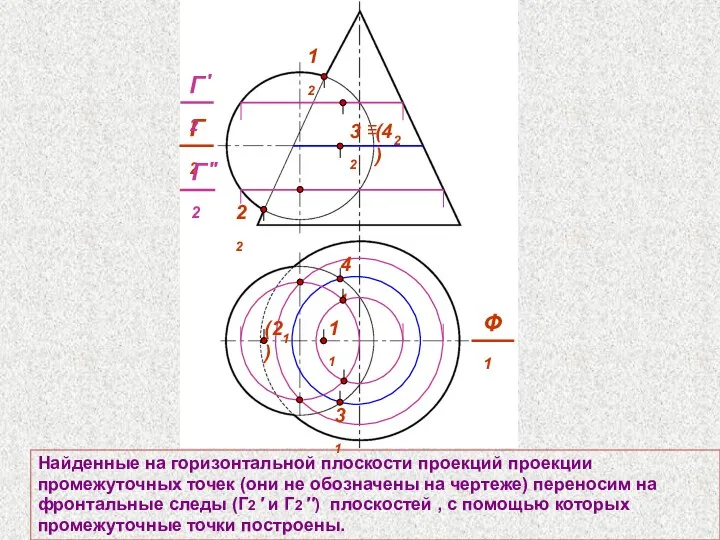
- 61. Найденные на горизонтальной плоскости проекций проекции промежуточных точек (они не обозначены на чертеже) переносим на фронтальные
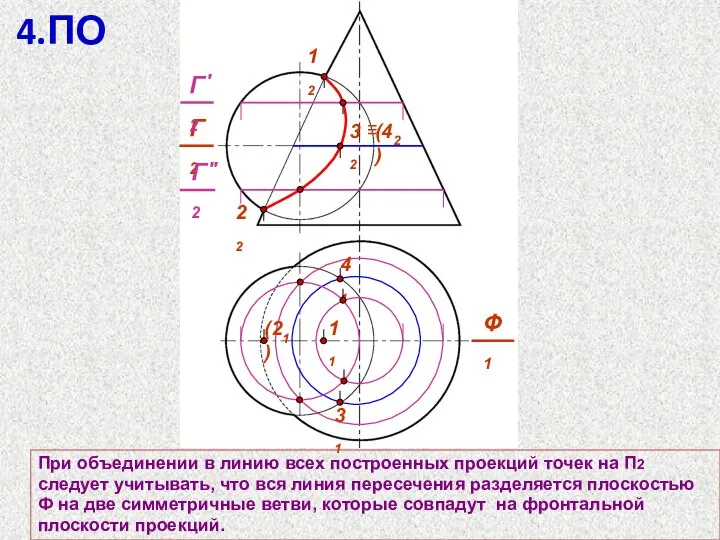
- 62. При объединении в линию всех построенных проекций точек на П2 следует учитывать, что вся линия пересечения
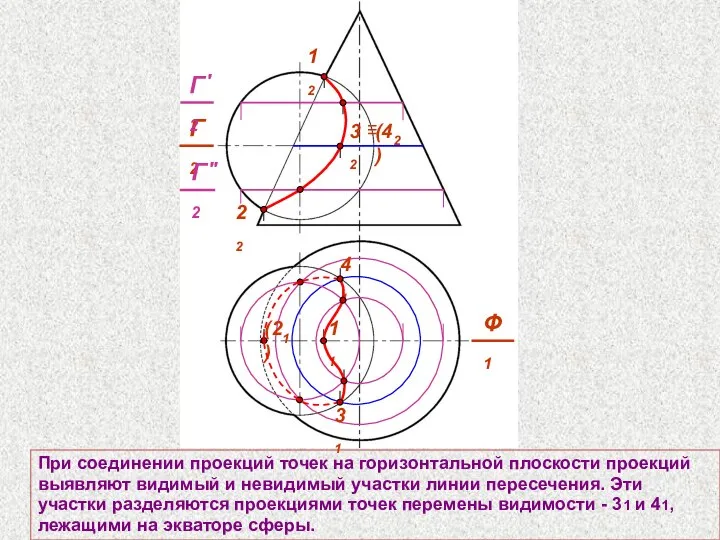
- 63. При соединении проекций точек на горизонтальной плоскости проекций выявляют видимый и невидимый участки линии пересечения. Эти
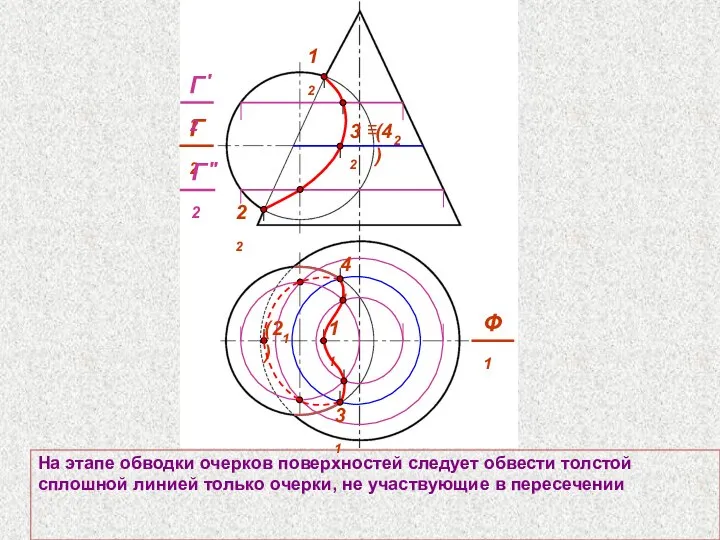
- 64. На этапе обводки очерков поверхностей следует обвести толстой сплошной линией только очерки, не участвующие в пересечении
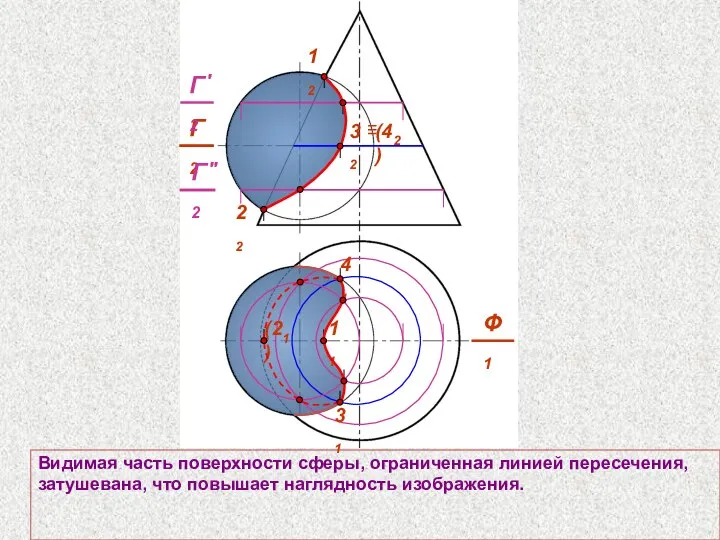
- 65. Видимая часть поверхности сферы, ограниченная линией пересечения, затушевана, что повышает наглядность изображения. 12 22 Ф1 (21)
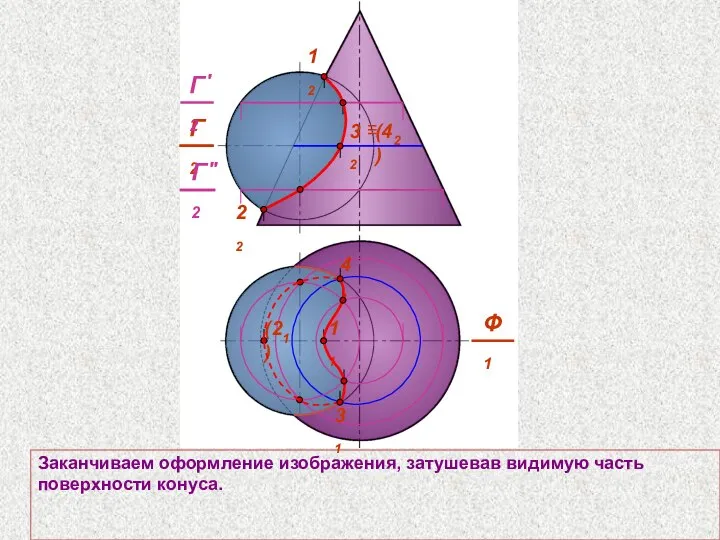
- 66. Заканчиваем оформление изображения, затушевав видимую часть поверхности конуса. 12 22 Ф1 (21) 11 Г2 31 41
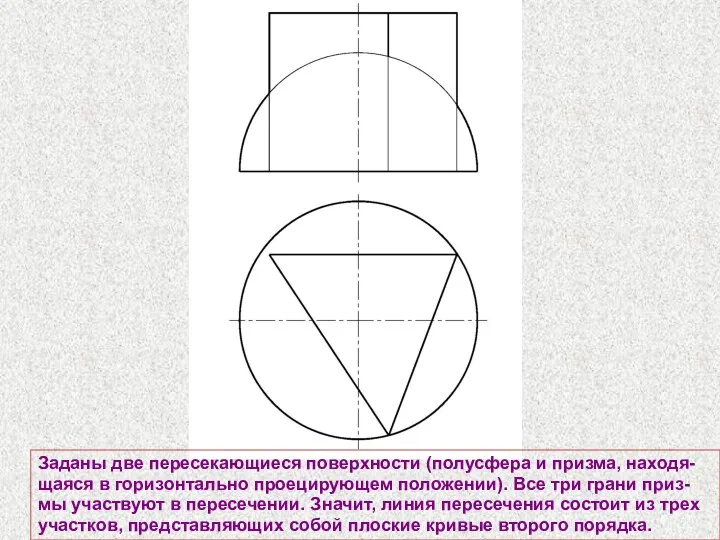
- 67. Заданы две пересекающиеся поверхности (полусфера и призма, находя-щаяся в горизонтально проецирующем положении). Все три грани приз-мы
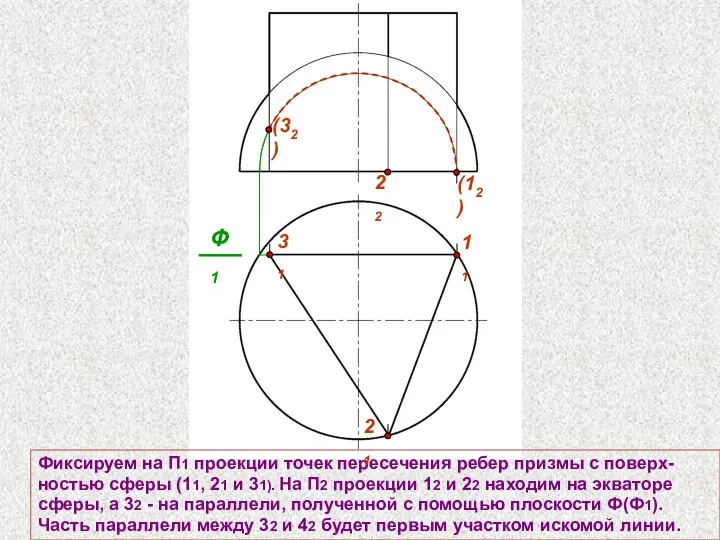
- 68. Фиксируем на П1 проекции точек пересечения ребер призмы с поверх- ностью сферы (11, 21 и 31).
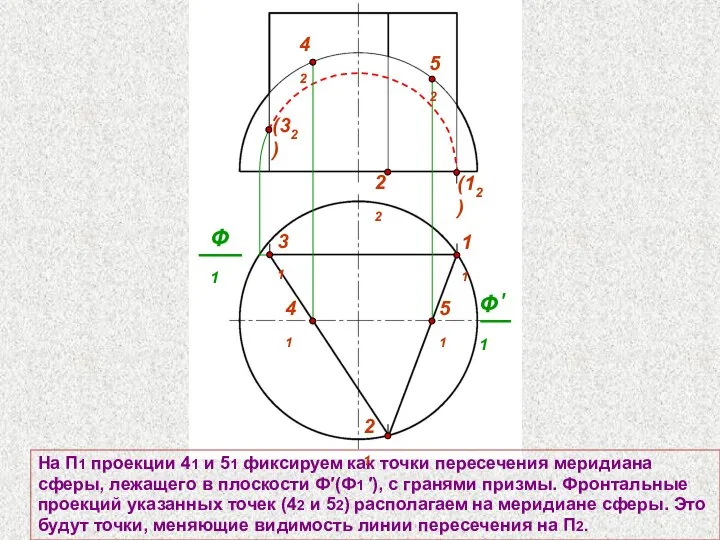
- 69. 31 11 На П1 проекции 41 и 51 фиксируем как точки пересечения меридиана сферы, лежащего в
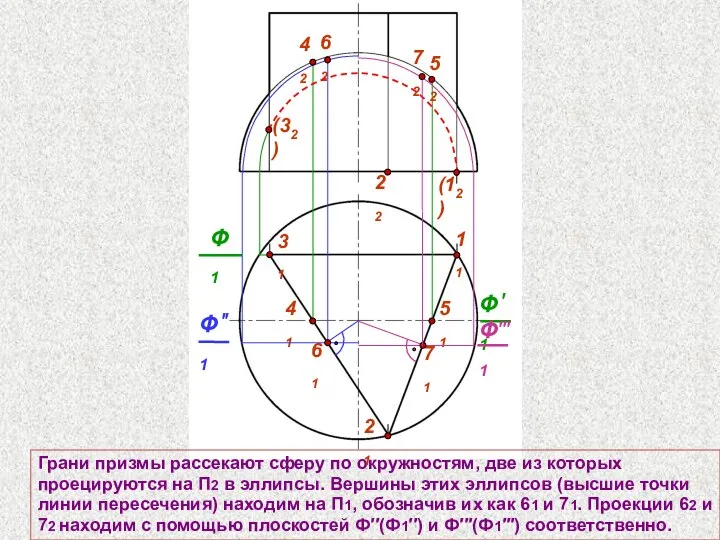
- 70. 31 11 Грани призмы рассекают сферу по окружностям, две из которых проецируются на П2 в эллипсы.
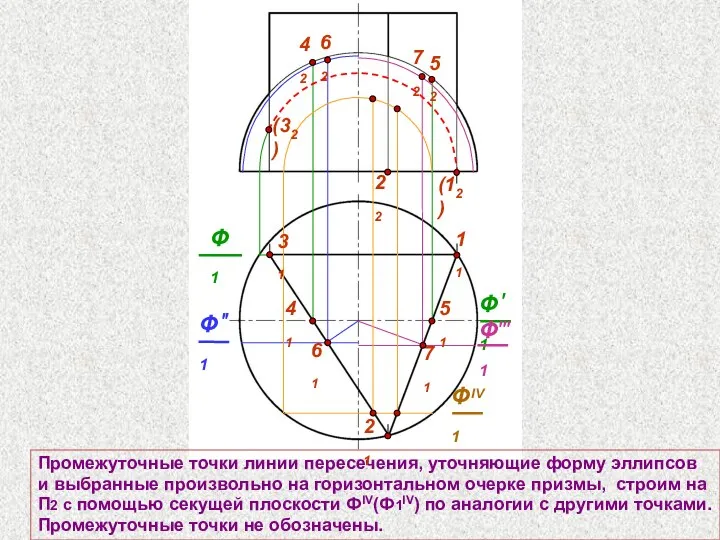
- 71. 22 Промежуточные точки линии пересечения, уточняющие форму эллипсов и выбранные произвольно на горизонтальном очерке призмы, строим
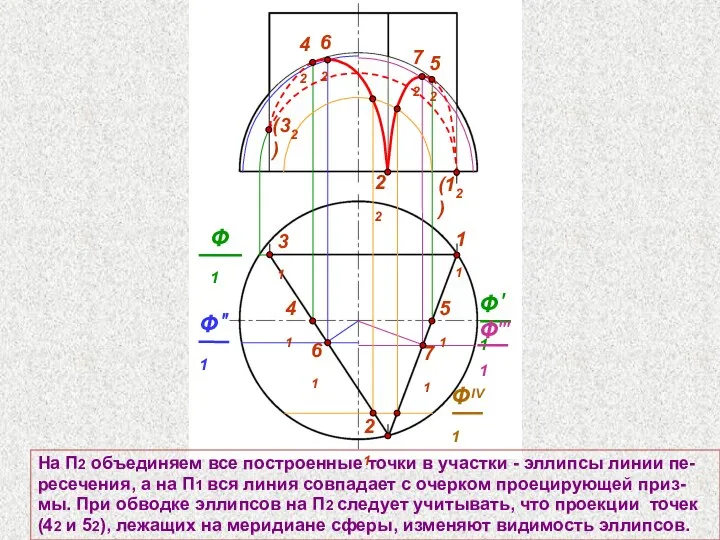
- 72. 22 31 На П2 объединяем все построенные точки в участки - эллипсы линии пе- ресечения, а
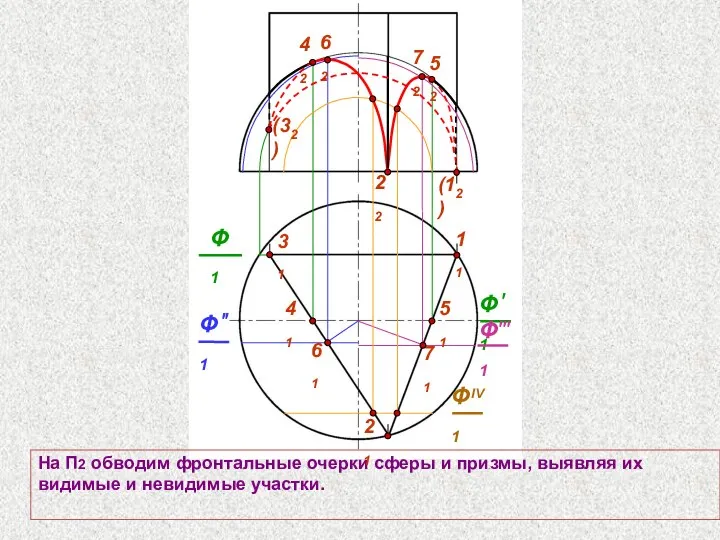
- 73. 22 31 На П2 обводим фронтальные очерки сферы и призмы, выявляя их видимые и невидимые участки.
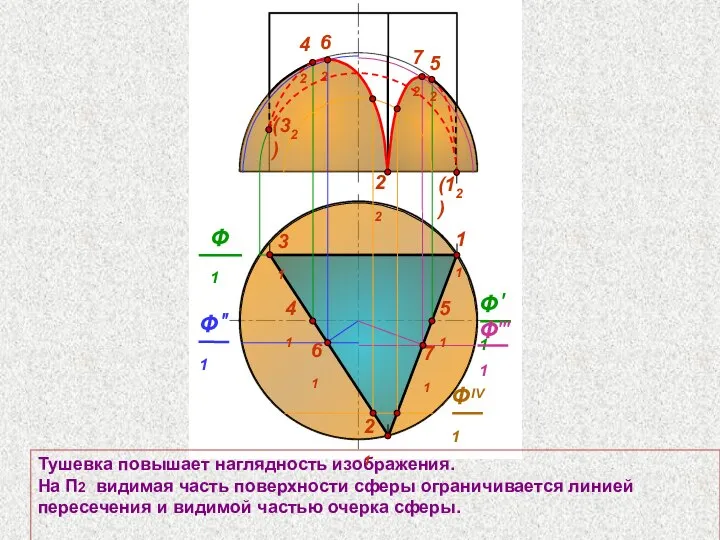
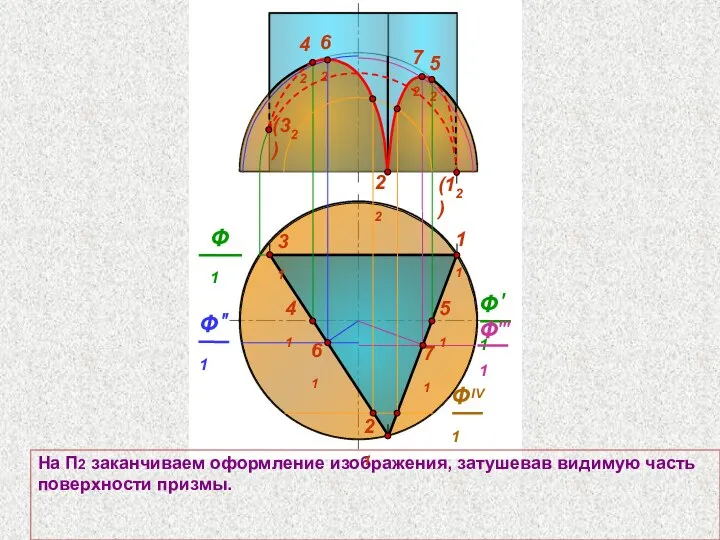
- 74. 22 31 Тушевка повышает наглядность изображения. На П2 видимая часть поверхности сферы ограничивается линией пересечения и
- 75. 22 31 На П2 заканчиваем оформление изображения, затушевав видимую часть поверхности призмы. 21 Ф1 42 52
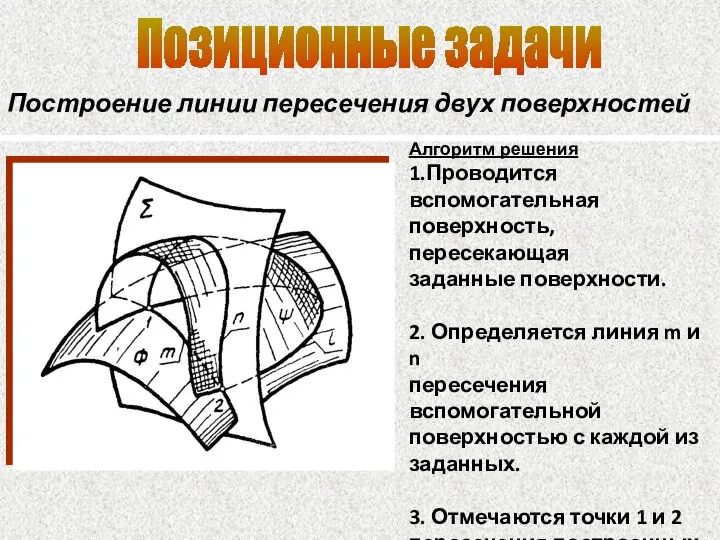
- 76. Позиционные задачи Построение линии пересечения двух поверхностей Алгоритм решения 1.Проводится вспомогательная поверхность, пересекающая заданные поверхности. 2.
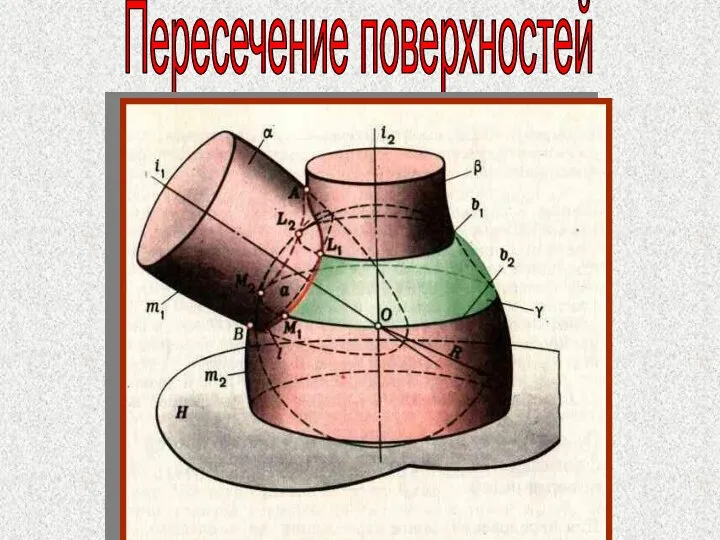
- 77. Пересечение поверхностей
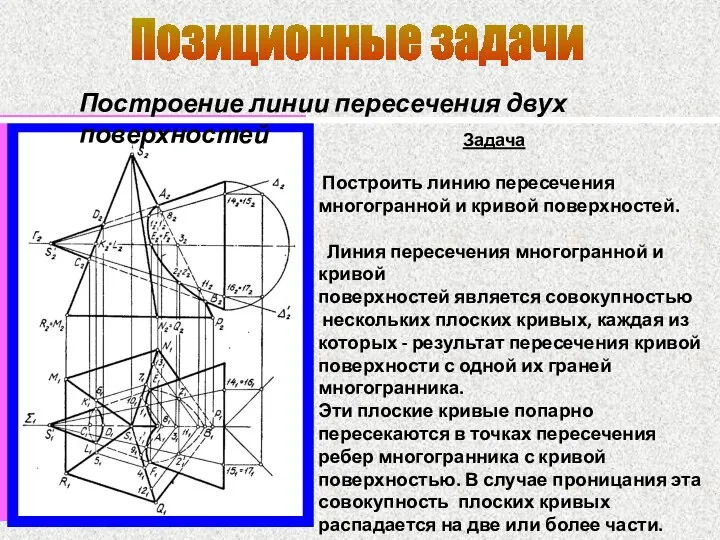
- 78. Позиционные задачи Построение линии пересечения двух поверхностей Задача Построить линию пересечения многогранной и кривой поверхностей. Линия
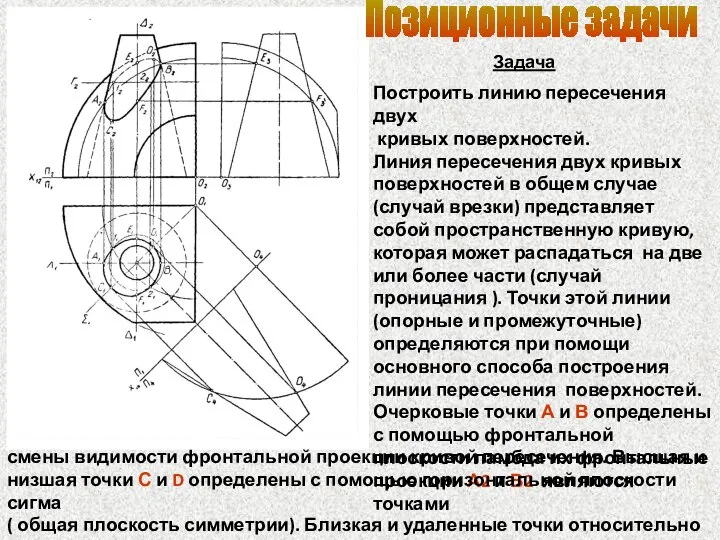
- 79. Задача Построить линию пересечения двух кривых поверхностей. Линия пересечения двух кривых поверхностей в общем случае (случай
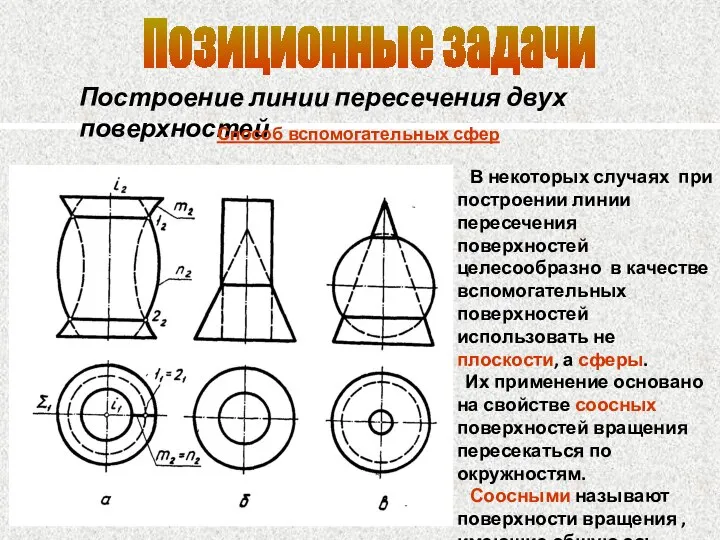
- 80. Позиционные задачи Построение линии пересечения двух поверхностей Способ вспомогательных сфер В некоторых случаях при построении линии
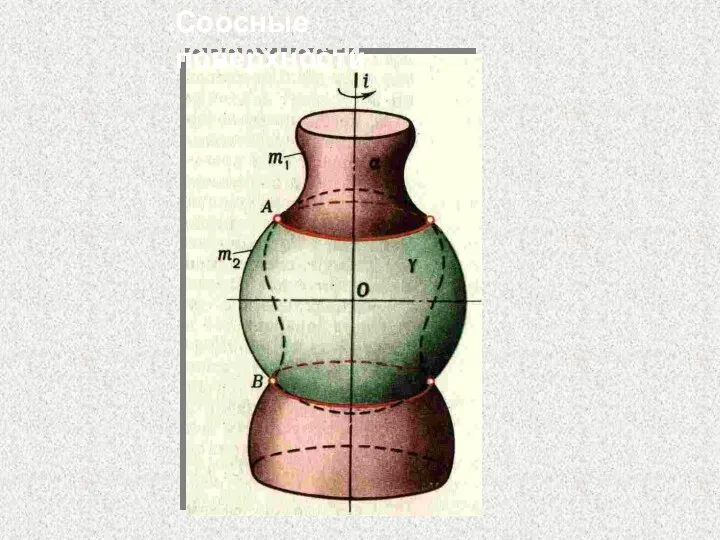
- 81. Соосные поверхности
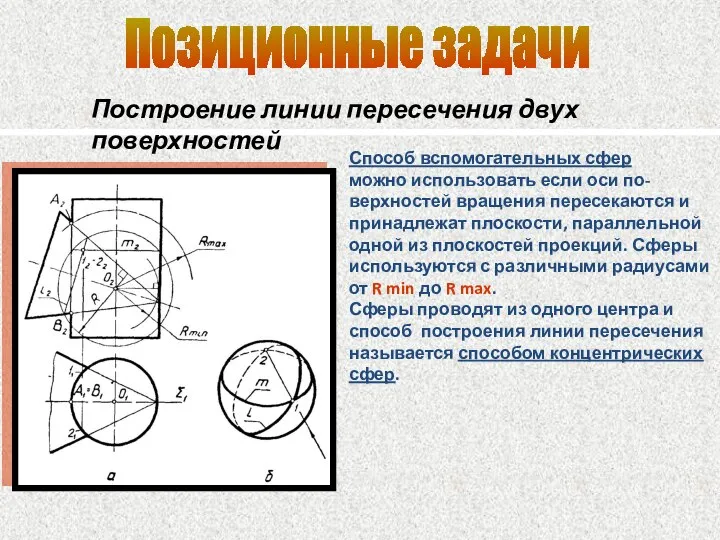
- 82. Позиционные задачи Построение линии пересечения двух поверхностей Способ вспомогательных сфер можно использовать если оси по- верхностей
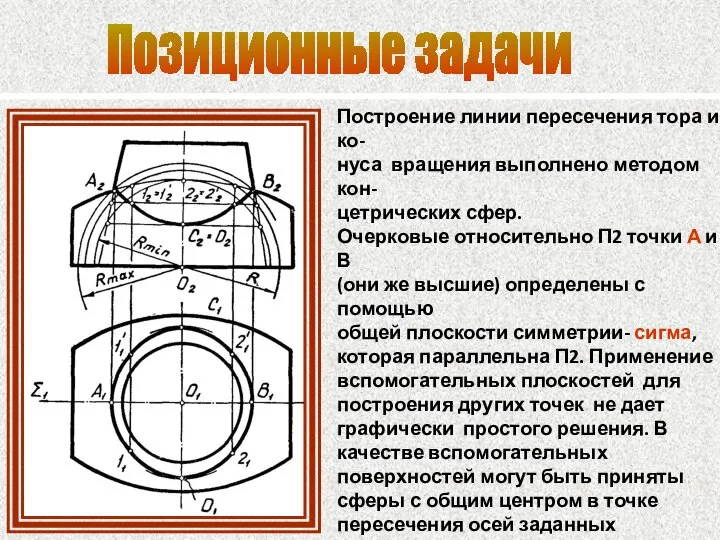
- 83. Позиционные задачи Построение линии пересечения тора и ко- нуса вращения выполнено методом кон- цетрических сфер. Очерковые
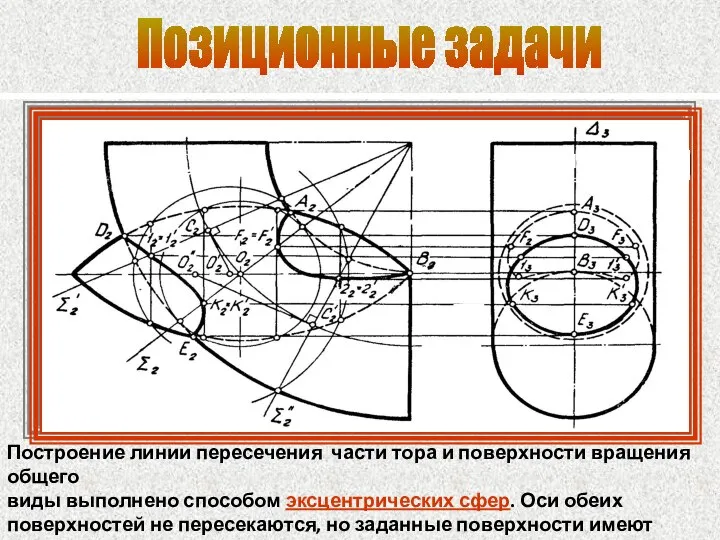
- 84. Позиционные задачи Построение линии пересечения части тора и поверхности вращения общего виды выполнено способом эксцентрических сфер.
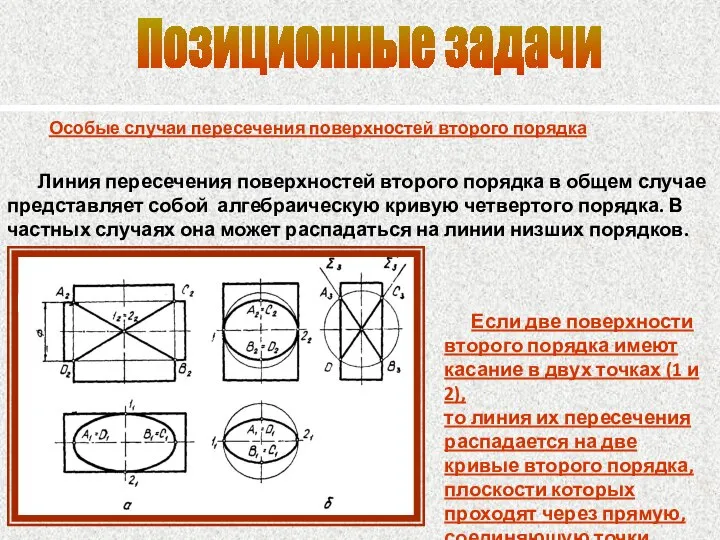
- 85. Позиционные задачи Особые случаи пересечения поверхностей второго порядка Линия пересечения поверхностей второго порядка в общем случае
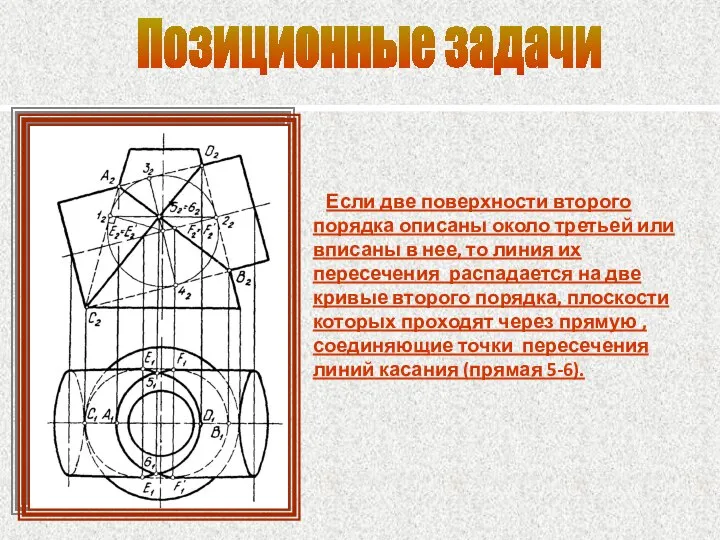
- 86. Позиционные задачи Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия
- 87. Позиционные задачи Пример построения пересечения многогранников
- 88. Позиционные задачи Примеры построения линий пересечения поверхностей
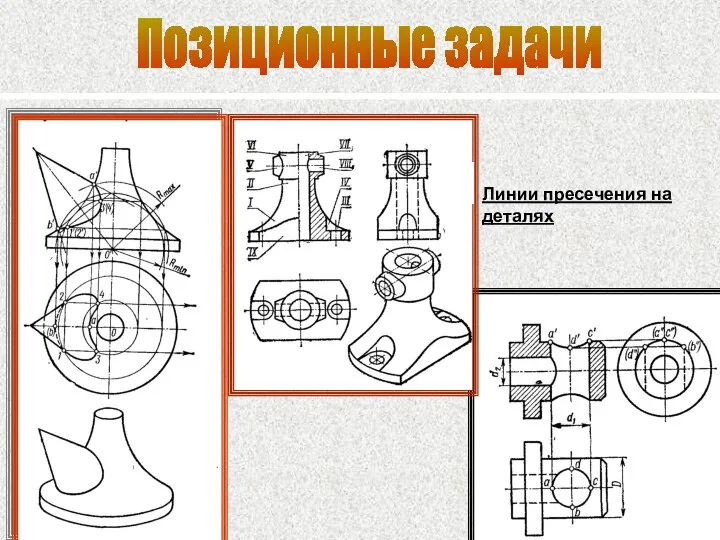
- 89. Позиционные задачи Линии пресечения на деталях
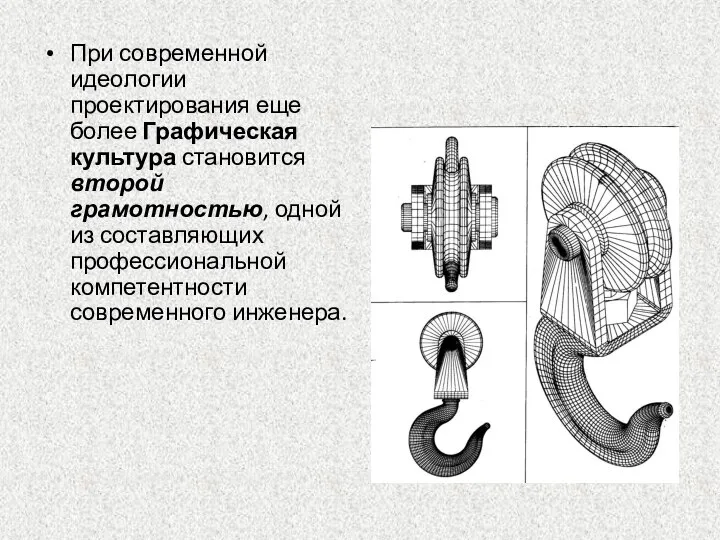
- 90. При современной идеологии проектирования еще более Графическая культура становится второй грамотностью, одной из составляющих профессиональной компетентности
- 91. Используемая литература Основная литература 1. Кострюков, А. В. Начертательная геометрия [Текст] : учеб. пособие по курсу
- 93. Скачать презентацию





















![Используемая литература Основная литература 1. Кострюков, А. В. Начертательная геометрия [Текст] :](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1049656/slide-90.jpg)
 Необычный отель
Необычный отель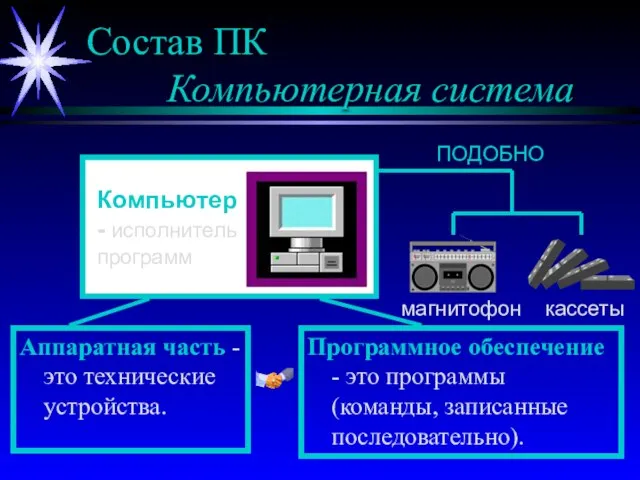 Состав ПК Компьютерная система
Состав ПК Компьютерная система 孔子学院在乌克兰和俄罗斯
孔子学院在乌克兰和俄罗斯 Places and Perspectives
Places and Perspectives Ресурси страховика
Ресурси страховика Метрическая система мер
Метрическая система мер Успешность адаптации ребенка при переходе со ступени начального образования – на основную
Успешность адаптации ребенка при переходе со ступени начального образования – на основную Istambek
Istambek Правила поведения итехники безопасности в кабинете информатики.
Правила поведения итехники безопасности в кабинете информатики. Город как среда обитания (5 класс)
Город как среда обитания (5 класс) Почему нужно чистить зубы?
Почему нужно чистить зубы? Автоматизированная система управления качеством вуза
Автоматизированная система управления качеством вуза Айдентика. Корпоративная идентификация
Айдентика. Корпоративная идентификация Повесть «Детство»
Повесть «Детство» Design Reboot
Design Reboot Клуб Алтын, доход посредством роста курса внутренней монеты
Клуб Алтын, доход посредством роста курса внутренней монеты Перспективы участия иностранных банков в развитии ритейлового бизнеса в российских регионах
Перспективы участия иностранных банков в развитии ритейлового бизнеса в российских регионах Работа с заданиями на анализ исторических версий и оценок.
Работа с заданиями на анализ исторических версий и оценок. Подготовка к ЕГЭ. (окончания глаголов и суффиксов причастий)
Подготовка к ЕГЭ. (окончания глаголов и суффиксов причастий) Проблемы начала правоприменения в сфере борьбы с картелями – опыт Бразилии
Проблемы начала правоприменения в сфере борьбы с картелями – опыт Бразилии Сложноподчиненные предложения с определительными придаточными
Сложноподчиненные предложения с определительными придаточными Фразеологическое ядро старославянского языка
Фразеологическое ядро старославянского языка План развития ЮФО 2020
План развития ЮФО 2020 Конструктивизм
Конструктивизм Мартиничка
Мартиничка Электронное портфолио ученика
Электронное портфолио ученика Магистерская программа 031100.68.20 Сопоставительное изучение культур и межкультурная коммуникация
Магистерская программа 031100.68.20 Сопоставительное изучение культур и межкультурная коммуникация Презентация на тему Украшение пасхального яйца
Презентация на тему Украшение пасхального яйца