МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ХИЩНИКИ-ЖЕРТВЫ

Материальные и информационные модели
1. Биологические предметные модели, служат для изучения общих биологических закономерностей, действий различных препаратов, методов лечения. К этому типу моделей относятся лабораторные животные, изолированные органы, культуры клеток. Этот вид моделирования, самый древний и играет большую роль в современной науке(первые полеты в космос, испытание новых лекарств и т. д.)

2. Физические (аналоговые) модели − это физические системы или устройства, которые обладают аналогичным с моделируемым объектом поведением. Физическая модель может быть реализована в виде некоторого механического устройства или в виде электрической цепи. Например, процесс движения крови по крупным сосудам может быть смоделирован электрической цепью из конденсаторов и сопротивлений.

3. Кибернетические модели − это различные устройства, в составе которых имеется блок управления − чаще всего компьютер, который моделирует информационные процессы в живом организме, среди которых самый распространенный − это управление. (Например, управление движением руки, всего тела или управление величиной зрачка). Сложность таких кибернетических моделей разная, вплоть до “искусственного интеллекта”, являющегося кибернетической моделью мозга человека.

4. Математическая модель – это система математических соотношений – формул, уравнений, неравенств и т.д., отражающих существенные свойства объекта или явления.

Этапы математического моделирования
1этап: создание основы математической модели. При этом нужно-
а) накопить экспериментальные данные о процессах в изучаемой системе,
б) составить уравнение или систему уравнений, описывающих закономерную связь данных.

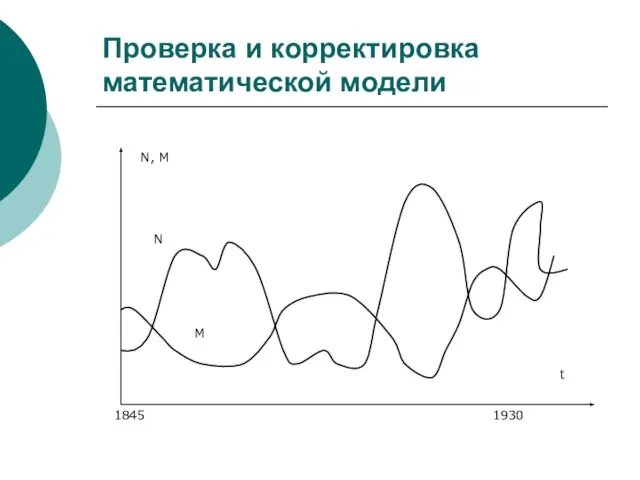
2 этап: проверка и корректировка модели. При этом необходимо:
а) определить численные значения коэффициентов и задать начальные условия,
б) решить систему уравнений,
в) сравнить полученное решение с данными эксперимента, выявить несоответствия, выяснить их причины,
г) ввести поправки в математическую модель.

3 этап: исследование математической модели, т.е. использование ее в практических целях
Конечной целью этого этапа является получение новой информации об исследуемом объекте.

Математическая модель “хищники - жертвы”
Впервые в биологии математическая модель периодического изменения числа особей антагонистических видов животных предложил итальянский математик В. Вольтерра с сотрудниками. Модель, предложенная Вольтерра, явилась развитием идеи, намеченной в 1924 году А. Лоттки в книге “Элементы физической биологии”. Поэтому данная классическая модель известна как “модель Лоттки-Вольтерра”.

Исходная задача
В некотором, экологически замкнутом районе, живут два вида животных (например, рыси и зайцы). Рыси (хищники) могут питаться только зайцами.

Исходная задача
Зайцы (жертвы) питаются растительной пищей, имеющейся всегда в достаточном количестве (в рамках данной модели не учитывается ограниченность ресурсов растительной пищи).

Исходная задача
Необходимо определить, как будет меняться численность жертв и хищников с течением времени в такой экологической системе.

Составление дифференциальных уравнений
Обозначим число жертв через N,
а число хищников через M.
Числа N и M являются функциями времени t.

В нашей модели учтем следующие факторы:
Естественное размножение жертв
Естественная гибель жертв
Уничтожение жертв за счет поедания их хищниками
Естественное вымирание хищников
Увеличение числа хищников за счет размножения при наличии пищи.

Так как речь идет о математической модели, то задачей является получение уравнений, в которые бы входили все намеченные факторы и которые описывали бы динамику, т.е. изменение числа хищников и жертв со временем.

Пусть за некоторое время ∆t количество жертв и хищников изменится на ∆N и ∆М. Изменение числа жертв ∆N за время ∆t определяется, во-первых, увеличением в результате естественного размножения (которое пропорционально количеству жертв);
(∆N)1=А N ∆t

(∆N)1=А N ∆t
где А - коэффициент пропорциональности, характеризующий скорость размножения жертв в данных условиях.

Во-вторых, имеет место уменьшение числа жертв из-за естественного вымирания, тоже пропорциональное их числу в данный момент:
(∆N)2= – В N ∆t
знак минус отражает именно уменьшение.

В основе вывода уравнения, описывающего уменьшение числа жертв из-за поедания их хищниками лежит идея о том , что чем чаще происходят их встречи , тем быстрее уменьшается число жертв.

Частота встреч хищника с жертвой пропорциональна и числу жертв и числу хищников, т.е. их произведению М·N

Поэтому можно записать:
(∆N)3= – C·M·N·∆t
Здесь коэффициент С характеризует частоту встреч жертвы с хищником.

В итоге с учетом всех трех факторов для изменения числа жертв можно записать следующее уравнение:
∆N=А·N·∆t – B·N·∆t – C·M·N·∆t

Поделив левую и правую часть уравнения на ∆t и перейдя к пределу при ∆t→0,
получим дифференциальное уравнение первого порядка:
dN/dt=A·N – B·N – C·M·N

Отметим, что левая часть уравнения является по смыслу “скоростью изменения числа жертв”, так как определяется как “изменение числа жертв ∆N за единицу времени ∆t.

Для того, чтобы решить это уравнение, нужно знать, как меняется число хищников М со временем.

Изменение числа хищников ∆M определяется увеличением из-за естественного размножения при наличии достаточного количества пищи ∆М1=Q·N·M·∆t
И уменьшением из-за естественного вымирания хищников
∆М2=-P·M·∆t

В итоге с учетом двух факторов для изменения числа хищников можно записать следующее уравнение:
∆М=Q·N·M·∆t - P·M·∆t

Поделив левую и правую часть уравнения на ∆t и перейдя к пределу при ∆t→0,
получим дифференциальное уравнение первого порядка
dM/dt=Q·M·N - P·M

Уравнения математической модели
dN/dt =A·N – B·N – C·M·N
dM/dt =Q·N·M – P·M

Данные дифференциальные уравнения представляют собой математическую модель “хищники - жертвы”. Достаточно определить значения коэффициентов А, В, С, Q, P и математическую модель можно использовать для решения поставленной задачи.

Проверка и корректировка математической модели

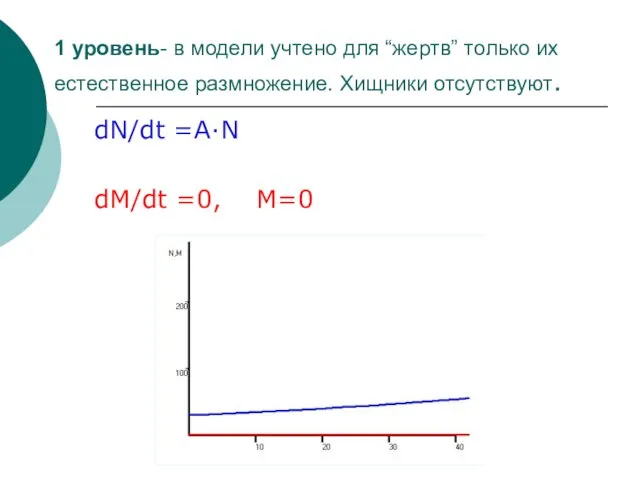
1 уровень- в модели учтено для “жертв” только их естественное размножение. Хищники отсутствуют.
dN/dt =A·N
dM/dt =0, M=0

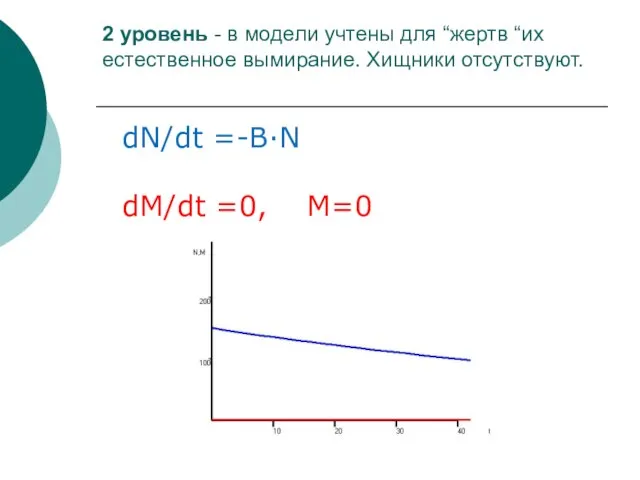
2 уровень - в модели учтены для “жертв “их естественное вымирание. Хищники отсутствуют.
dN/dt =-B·N
dM/dt =0, M=0

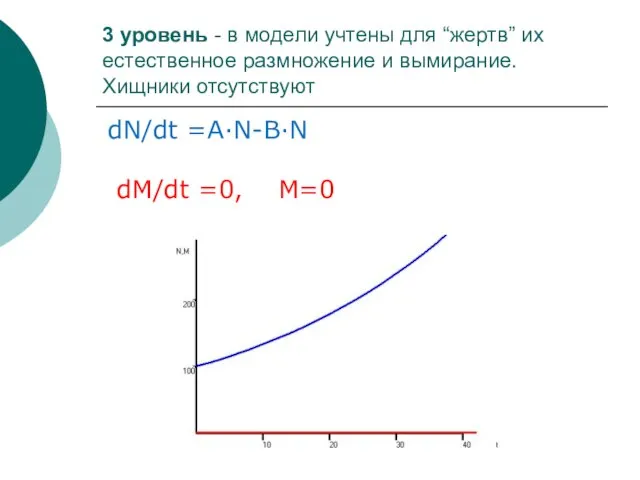
3 уровень - в модели учтены для “жертв” их естественное размножение и вымирание. Хищники отсутствуют
dN/dt =A·N-B·N
dM/dt =0, M=0

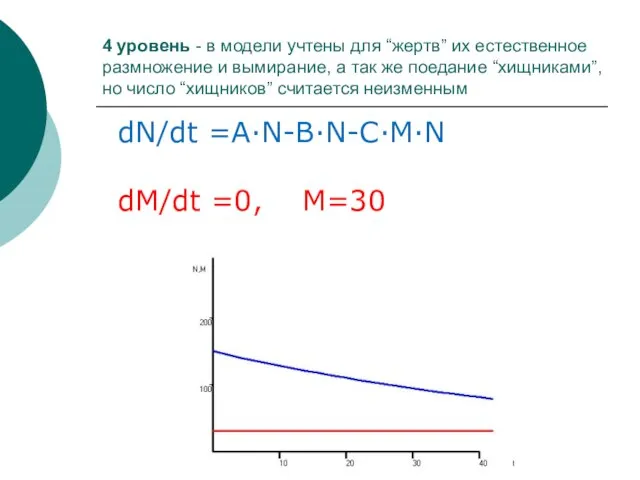
4 уровень - в модели учтены для “жертв” их естественное размножение и вымирание, а так же поедание “хищниками”, но число “хищников” считается неизменным
dN/dt =A·N-B·N-C·M·N
dM/dt =0, M=30

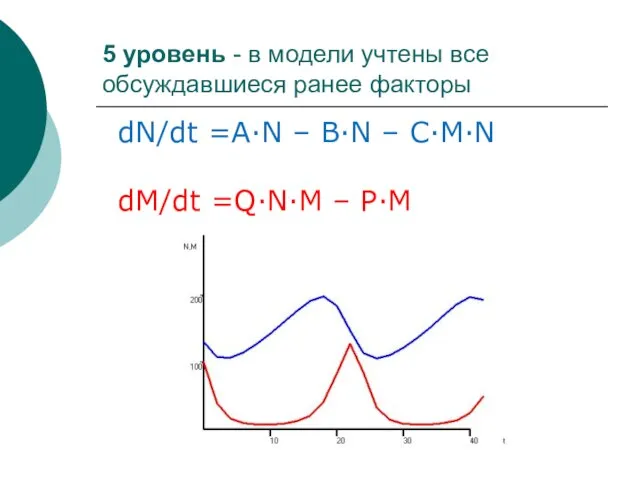
5 уровень - в модели учтены все обсуждавшиеся ранее факторы
dN/dt =A·N – B·N – C·M·N
dM/dt =Q·N·M – P·M