Содержание
- 2. Классическая педагогика прошлого утверждала – «Смертный грех учителя-быть скучным». Когда ребенок занимается из-под палки,он доставляет учителю
- 3. Активизация познавательной деятельности ученика без развития его познавательного интереса не только трудна, но практически и невозможна.
- 4. Сегодня, когда дети с самого раннего возраста развиваются в условиях новой информационной среды: использование телевидения, интернета,
- 5. Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как поддержать интерес к изучаемому материалу
- 6. Необходимо позаботиться о том, чтобы на уроках каждый ученик работал активно и увлечённо, и использовать это
- 7. Для нас стало очевидным, что используя только традиционные методы обучения, решить эту проблему невозможно, следует формировать
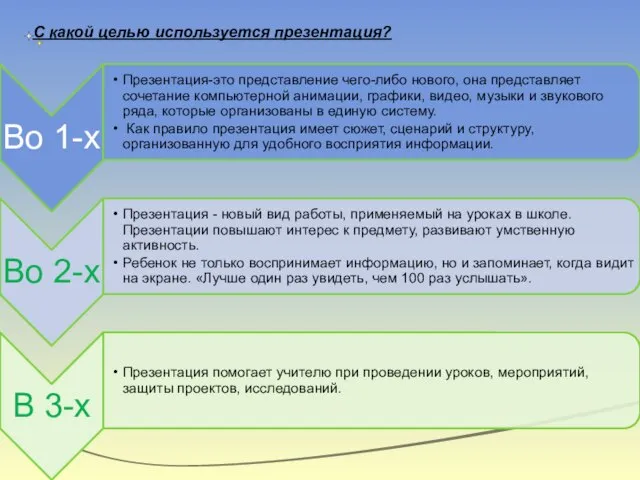
- 8. Одним из путей решения этой проблемы является создание и использование презентаций, которые на современном этапе развития
- 9. Использование презентационных материалов на уроках математики помогает: рационализировать формы преподнесения информации повысить степень наглядности; получить быструю
- 10. С какой целью используется презентация?
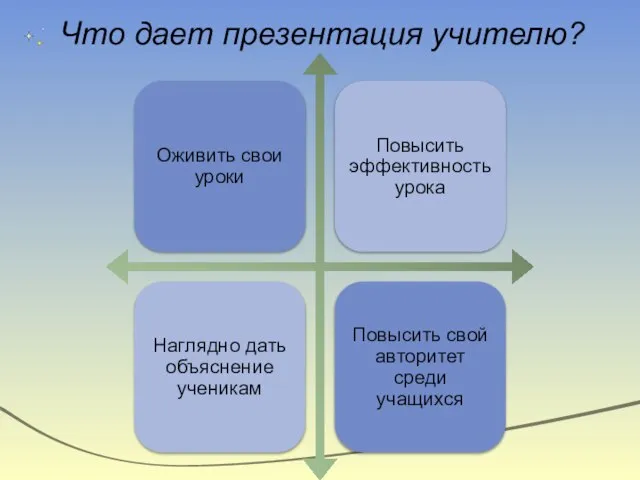
- 11. Что дает презентация учителю?
- 12. Однако следует помнить, что использование презентации, как и любое использование компьютерных технологий, должно быть оправдано. То
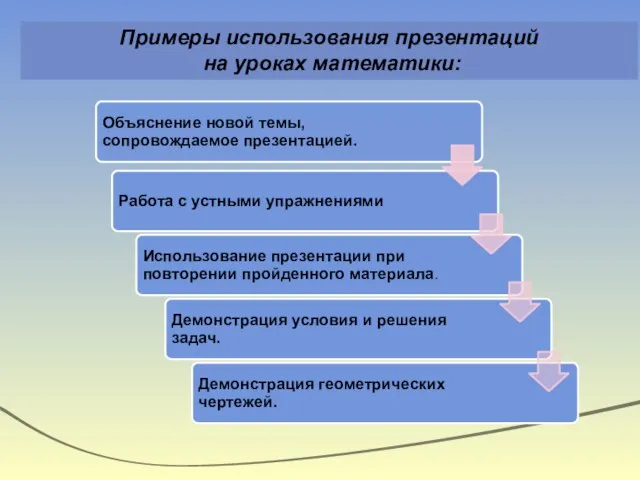
- 13. Примеры использования презентаций на уроках математики:
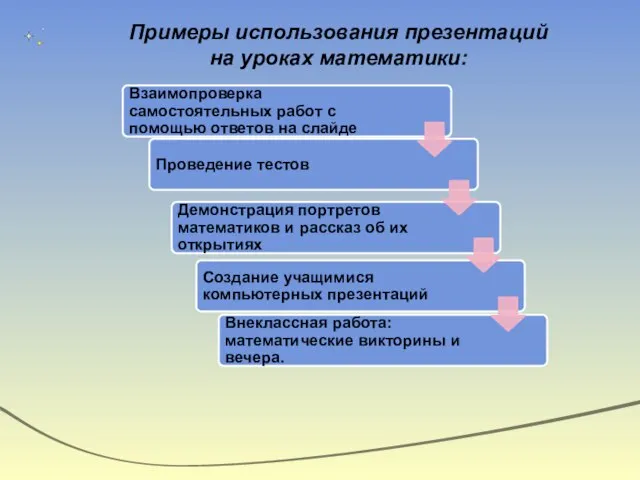
- 14. Примеры использования презентаций на уроках математики:
- 15. Объяснение новой темы, сопровождаемое презентацией. позволяет учителю расширить возможности обычной лекции, иллюстрировать тему разнообразными наглядными средствами,
- 16. Работа с устными упражнениями Устные упражнения активизируют мыслительную деятельность учащихся, развивают внимание, наблюдательность, память, речь, быстроту
- 17. Практическая задача. 152 544 384 Верно! Не верно! Подумай! Длина ограды школы 464 метра. Найдите ширину
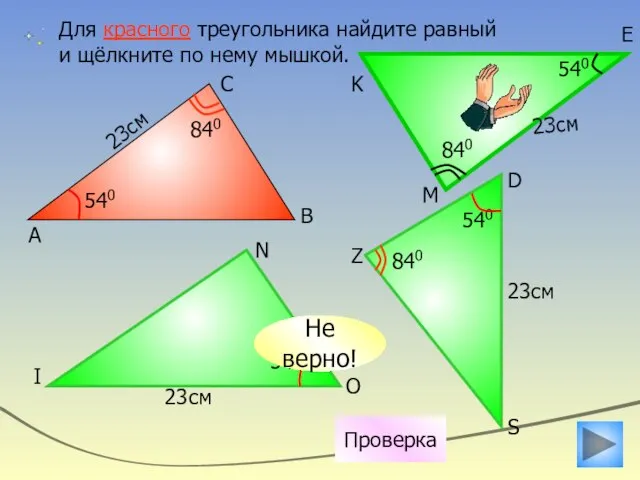
- 18. 23см 540 Для красного треугольника найдите равный и щёлкните по нему мышкой. 23см 23см 540 23см
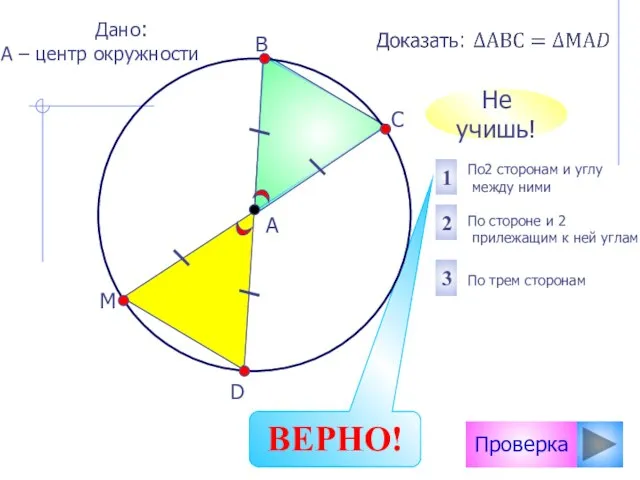
- 19. Проверка По2 сторонам и углу между ними По стороне и 2 прилежащим к ней углам По
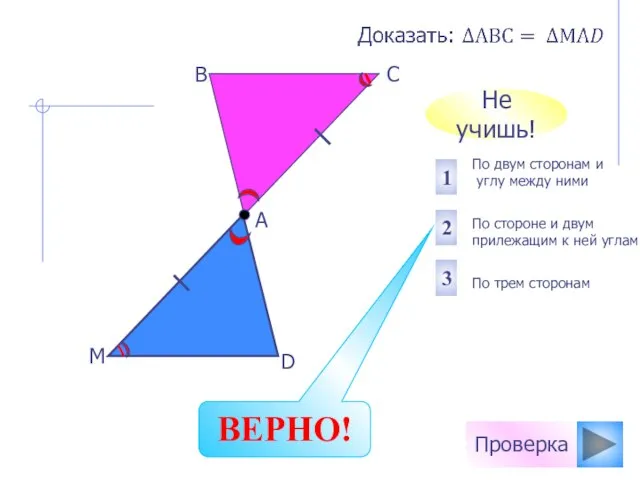
- 20. Проверка По двум сторонам и углу между ними По стороне и двум прилежащим к ней углам
- 21. Сформулируйте определение степени числа с натуральным показателем Сформулируйте свойство умножения степеней с одинаковыми основаниями Сформулируйте свойство
- 22. Мозговой штурм
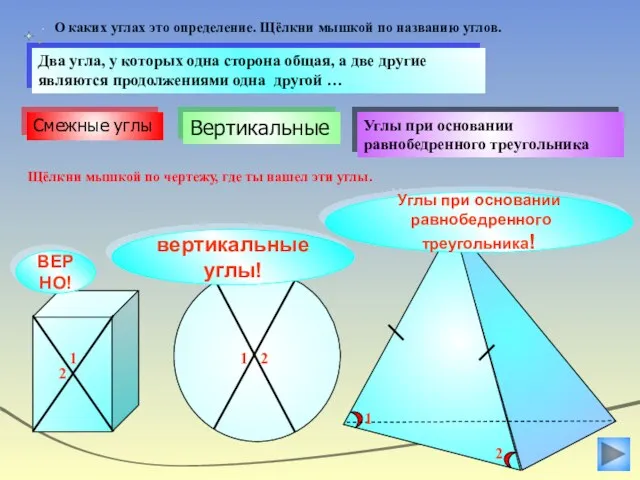
- 23. Какие углы называются смежными? Два угла. У которых одна сторона общая, а две другие являются продолжением
- 24. Углы при основании равнобедренного треугольника Вертикальные Два угла, у которых одна сторона общая, а две другие
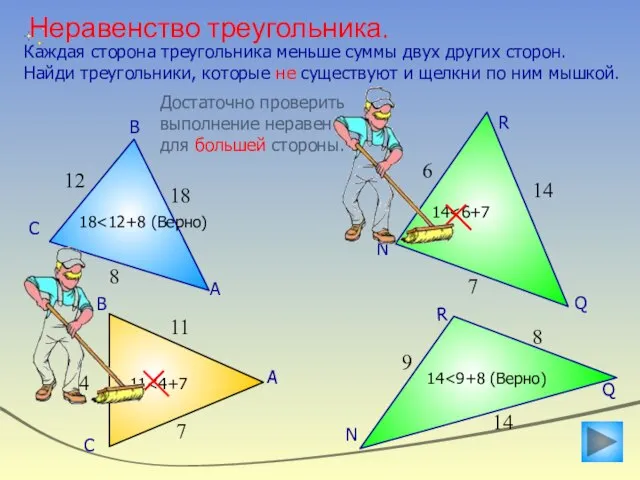
- 25. Неравенство треугольника. Каждая сторона треугольника меньше суммы двух других сторон. Найди треугольники, которые не существуют и
- 26. Демонстрация условия и решения задач. Компьютер значительно расширяет возможности предъявления учебной информации. Применение цвета, графики, звука,
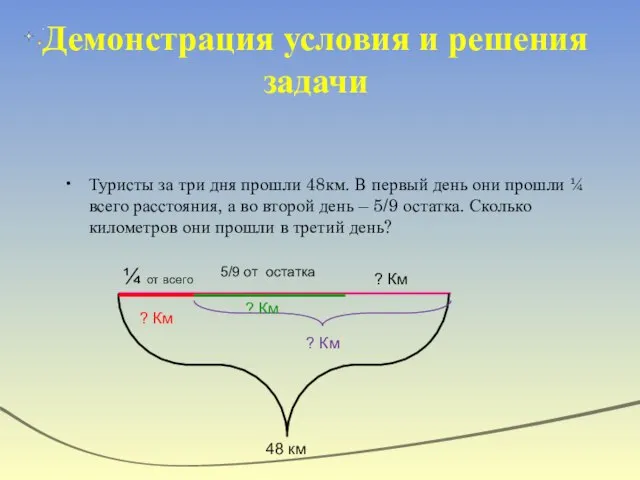
- 27. Демонстрация условия и решения задачи Туристы за три дня прошли 48км. В первый день они прошли
- 28. Решение Туристы за три дня прошли 48км. В первый день они прошли ¼ всего расстояния, а
- 29. Например, решить уравнение: х - 3 Х равное 3 обращает знаменатель в нуль, значит уравнение корней
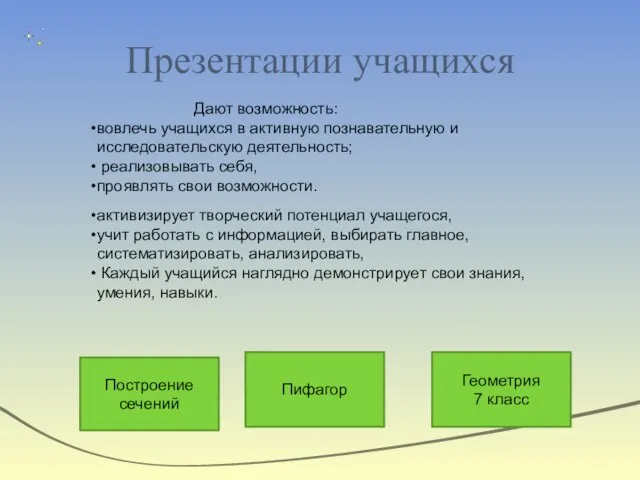
- 30. Презентации учащихся Построение сечений Пифагор Геометрия 7 класс Дают возможность: вовлечь учащихся в активную познавательную и
- 31. Взаимопроверка самостоятельных работ с помощью ответов на слайде Дает возможность оперативно проконтролировать и оценить результаты обучения.
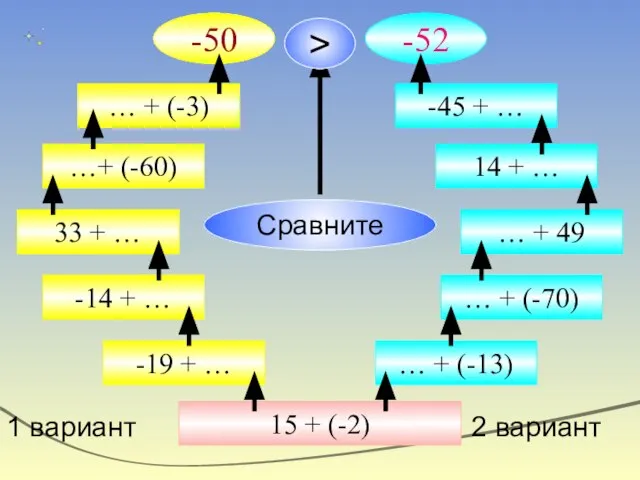
- 32. 15 + (-2) 1 вариант 2 вариант -19 + … -14 + … 33 + …
- 33. Математический диктант Проверьте себя: 30 900 106 2,5 0,03 1 вариант 40 800 104 3,5 0,03
- 34. Демонстрация геометрических чертежей. При решении задач обучающего характера компьютер помогает: выполнить рисунок, составить план работы, контролировать
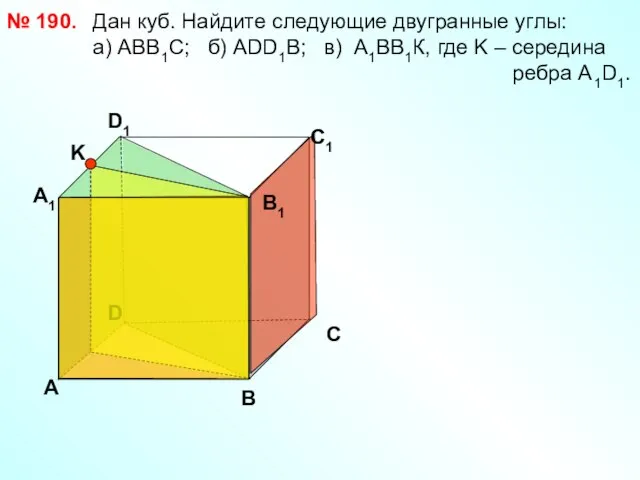
- 35. Дан куб. Найдите следующие двугранные углы: a) АВВ1С; б) АDD1B; в) А1ВВ1К, где K – середина
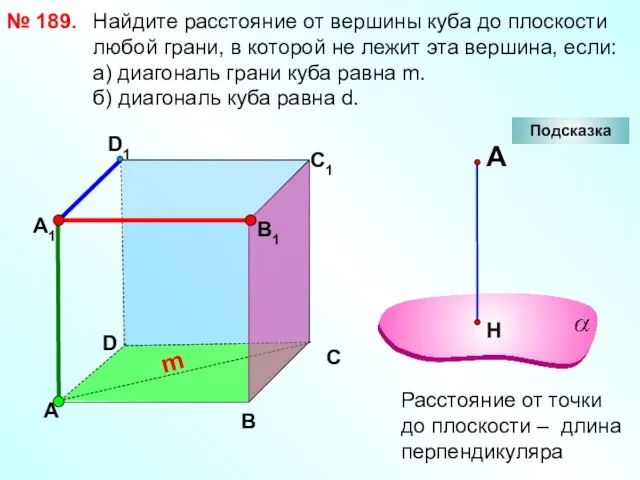
- 36. Найдите расстояние от вершины куба до плоскости любой грани, в которой не лежит эта вершина, если:
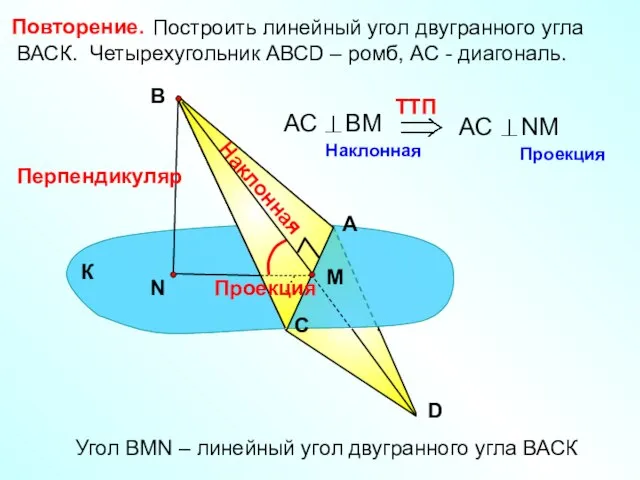
- 37. Построить линейный угол двугранного угла ВАСК. Четырехугольник АВСD – ромб, АС - диагональ. А С В
- 38. Подготовка к ГИА и ЕГЭ
- 41. Подготовка к ГИА и ЕГЭ MA-9_ДЕМО 2011 ГИА 9 от 17 февраля 2011 Одним из критериев
- 42. B4 из диагностической работы за 03.03.2011г
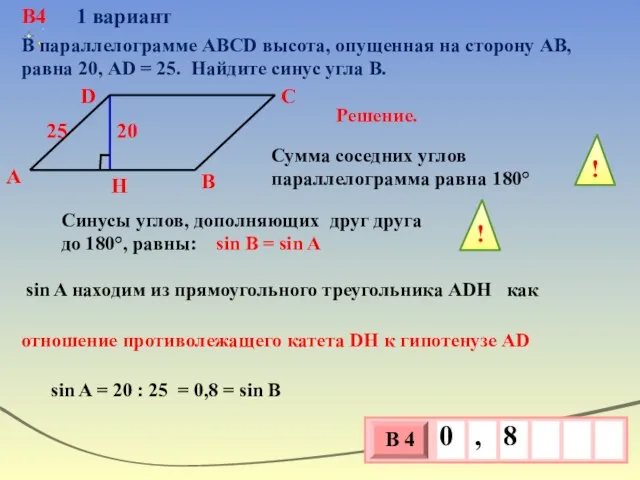
- 43. В4 1 вариант В С А H D В параллелограмме АВСD высота, опущенная на сторону АВ,
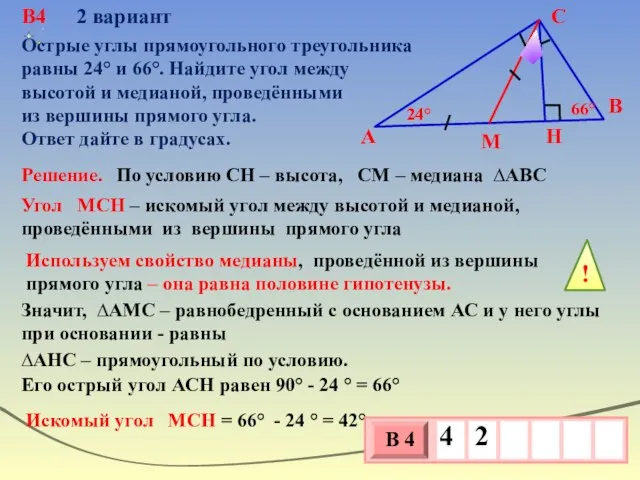
- 44. В4 2 вариант В С А H М Острые углы прямоугольного треугольника равны 24° и 66°.
- 45. Демонстрация портретов математиков и рассказ об их открытиях
- 46. 1.Кто из них сказал: «Математика – царица всех наук, а арифметика – царица математики»?
- 47. Карл Фридрих Гаусс – «король арифметики» Карл Гаусс (1777 – 1855) Немецкий математик, астроном, физик, геодезист.
- 48. 2.Кому принадлежат эти строки: «Математику уже затем учить надо, что она ум в порядок приводит»?
- 49. Михаил Васильевич Ломоносов Михаил Васильевич Ломоносов (1711 – 1765) - великий ученый: химик, физик, математик, поэт,
- 50. Колмогоров Андрей Николаевич Доктор физико-математических наук, профессор Московского Государственного Университета (1931), академик Академии Наук СССР (1939),
- 51. Информационные технологии открывают новые возможности для совершенствования учебного процесса,активизируют познавательную деятельность учеников и позволяют организовывать самостоятельную
- 53. Скачать презентацию
































 Первая помощь при кровотечениях
Первая помощь при кровотечениях Пожарная безопасность
Пожарная безопасность Коммуникационная политика
Коммуникационная политика Организация производства в основных цехах промышленных предприятий водного транспорта. Лекция 7
Организация производства в основных цехах промышленных предприятий водного транспорта. Лекция 7 Моя зеленоглазая комета
Моя зеленоглазая комета Натиск с Запада
Натиск с Запада ЧеловеческиеРасы
ЧеловеческиеРасы Образы для школы
Образы для школы Презентация на тему 300 лет Нижегородской Губернии
Презентация на тему 300 лет Нижегородской Губернии  Пейзаж, живопись
Пейзаж, живопись Предметно-пространственная среда в эпоху ренессанса
Предметно-пространственная среда в эпоху ренессанса Презентация на тему: Этика, право и менеджмент в стоматологии
Презентация на тему: Этика, право и менеджмент в стоматологии Презентация на тему Влияние деятельности человека на биосферу
Презентация на тему Влияние деятельности человека на биосферу А.С. Пушкин. Мой портрет
А.С. Пушкин. Мой портрет Автоматические устройства, история и современность
Автоматические устройства, история и современность Традиционная народная кукла. Изготовление куклы
Традиционная народная кукла. Изготовление куклы Презентация на тему Города-миллионеры
Презентация на тему Города-миллионеры Поверхностно-активные вещества
Поверхностно-активные вещества Собор Парижской Богоматери 9 класс
Собор Парижской Богоматери 9 класс Дома
Дома КОЛЫБЕЛИ НАДЕЖДЫ:право на жизнь для новорожденных в Украине
КОЛЫБЕЛИ НАДЕЖДЫ:право на жизнь для новорожденных в Украине IT- парк в Твери
IT- парк в Твери Религия и её место в жизни древних греков
Религия и её место в жизни древних греков Релігія і культура Давнього Китаю
Релігія і культура Давнього Китаю Пластический и энергетический обмен. Обмен органических веществ
Пластический и энергетический обмен. Обмен органических веществ Внедряйте CRM - режьте cost-ы. Высокая эффективность - залог успеха Сервиса Taxi 7220
Внедряйте CRM - режьте cost-ы. Высокая эффективность - залог успеха Сервиса Taxi 7220 Итальянский стиль в интерьере
Итальянский стиль в интерьере Первые Романовы. Начало
Первые Романовы. Начало