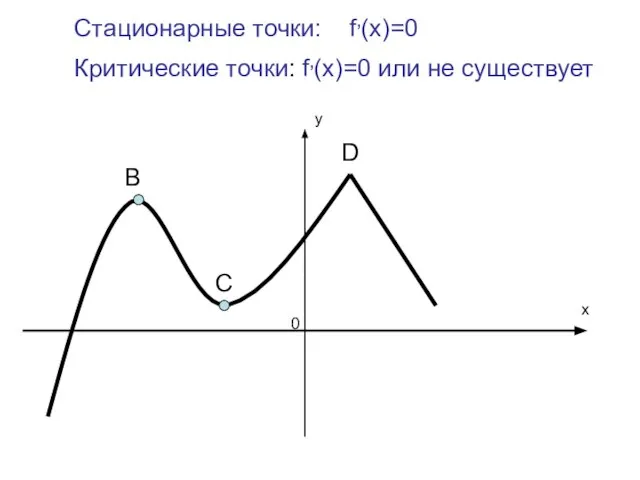
Слайд 2В
С
D
x
0
Стационарные точки: f,(x)=0
Критические точки: f,(x)=0 или не существует
у
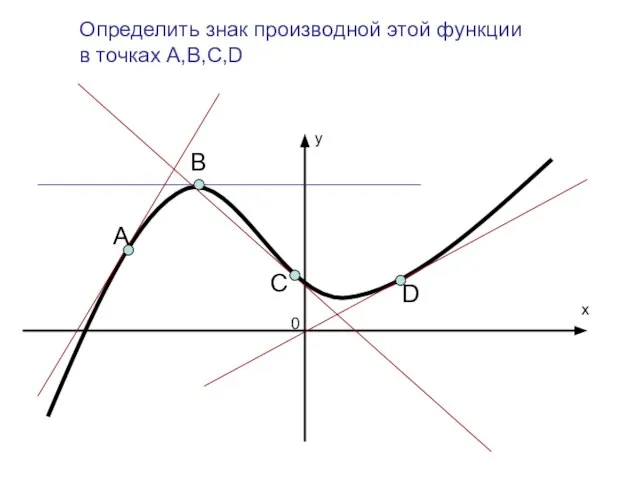
Слайд 3А
В
С
D
x
y
0
Определить знак производной этой функции
в точках А,В,С,D
Слайд 4Схема исследования функции на монотонность
Пусть дана функция f(x).
Находим область определения данной функции

D(f).
Находим ее производную f,(x).
Отыскиваем критические точки
(f,(x)=0 при х-?; f,(x) не существует при х-?).
4. Разбиваем область определения критическими точками на интервалы.
5. Выясняем знак производной на каждом интервале.
6. Делаем вывод: f,(x)>0, f(x) на….
f,(x)<0, f(x) на …..
Слайд 50
х
у
Ответ: f(x) на
и на
Внимание!
Если при исследовании функции на монотонность

мы получаем не один, а несколько интервалов, где производная , к примеру меньше нуля, то функция убывает не на объединении этих интервалов, а на каждом из них.




 Предквантум
Предквантум Старинные зимние обычаи и праздники, «Рождество», «Святки»
Старинные зимние обычаи и праздники, «Рождество», «Святки» ВИДЕО-СТЕНА DIBOSS LB-40
ВИДЕО-СТЕНА DIBOSS LB-40 Новый подход к интеграции календарно-сетевых графиков и смет
Новый подход к интеграции календарно-сетевых графиков и смет Областной конкурс Методическая разработка дистанционного урока - 2021
Областной конкурс Методическая разработка дистанционного урока - 2021 Музей путешествий. Поклонная гора. Парк Победы
Музей путешествий. Поклонная гора. Парк Победы Товары и услуги
Товары и услуги Техническое регулирование
Техническое регулирование 20140305_lekarstvennye_rasteniya_buturlinovskogo_rayona
20140305_lekarstvennye_rasteniya_buturlinovskogo_rayona Консолидация ритейла в Украине: роль логистики 1.Предпосылки для консолидации ритейла 2.Когда ритейлеру нужен 3PL-оператор? 3.Case study 4.
Консолидация ритейла в Украине: роль логистики 1.Предпосылки для консолидации ритейла 2.Когда ритейлеру нужен 3PL-оператор? 3.Case study 4. Project on the Indian Ocean
Project on the Indian Ocean  Портретная студийная съёмка
Портретная студийная съёмка Внешняя политика Советского государства 1920-х
Внешняя политика Советского государства 1920-х СТРОКА, ОБОРВАННАЯ ПУЛЕЙ
СТРОКА, ОБОРВАННАЯ ПУЛЕЙ ЕГЭ В 3 «Площади»
ЕГЭ В 3 «Площади» Цветовой контраст (хроматический)
Цветовой контраст (хроматический) Фотожурналист Владимир Вяткин
Фотожурналист Владимир Вяткин 26-27 апреля 2006 года Центр практической психологии РГУ имени С.А. Есенина Московский городской психолого-педагогический университе
26-27 апреля 2006 года Центр практической психологии РГУ имени С.А. Есенина Московский городской психолого-педагогический университе Кейс-стади для педагогов
Кейс-стади для педагогов Об аксиомах геометрии
Об аксиомах геометрии Презентация на тему Родная природа в стихотворениях поэтов xx века
Презентация на тему Родная природа в стихотворениях поэтов xx века  Каталог Атоми
Каталог Атоми Особенности организации и проведения школьного этапа Всероссийской олимпиады школьников по русскому языку Соловьева Т.В., предсе
Особенности организации и проведения школьного этапа Всероссийской олимпиады школьников по русскому языку Соловьева Т.В., предсе Создание новогодней открытки на основе пейзажа «Зимние россыпи»
Создание новогодней открытки на основе пейзажа «Зимние россыпи» Внесем порядок в хаос! ИЗО 7 класс
Внесем порядок в хаос! ИЗО 7 класс Космонавты, рожденные Украиной: космонавты Луганщины
Космонавты, рожденные Украиной: космонавты Луганщины Межрегиональный образовательный форум «Открытое образовательное пространство: живая праКтика тьюторства»
Межрегиональный образовательный форум «Открытое образовательное пространство: живая праКтика тьюторства» ДДК. Экскурсия
ДДК. Экскурсия