Содержание
- 2. Правило Лопиталя Рассмотрим отношение двух функций Будем говорить, что это отношение при есть неопределенность вида если
- 3. Если существует то вычисление этого предела называют раскрытием упомянутой неопределенности.
- 4. Неопределенность вида В случае когда функции стремятся к бесконечности при , также применимо правило Лопиталя. Справедливо
- 5. Пример. Вычислить пределы: Решение.
- 6. Решение.
- 7. Решение.
- 8. Точка называется точкой локального максимума функции f(x), если в некоторой окрестности точки выполняется неравенство Точка называется
- 9. Общий термин для локального максимума и локального минимума – локальный экстремум. Необходимое условие экстремума дифференцируемой функции:
- 10. Точки, в которых производная функции обращается в нуль или не существует, называются критическими (или стационарными).
- 11. Первое достаточное условие экстремума Пусть функция f(x) непрерывна в некотором интервале, содержащем критическую точку, и дифференцируема
- 12. Исследование функции на экстремум с помощью первой производной 1. Найти производную 2. Найти критические точки. 3.
- 13. Пример. Исследовать функцию на экстремум: Решение. Найдем производную: - критические точки
- 14. Исследуем знак производной: - точки локального минимума; - минимальные значения функции;
- 15. точка локального максимума, - максимальное значение функции в этой точке.
- 16. Наибольшее и наименьшее значения функции на отрезке Наибольшее или наименьшее значение функции может достигаться как в
- 17. Схема для нахождения наибольшего и наименьшего значений функции на отрезке: 1. Найти производную 2. Найти критические
- 18. Пример. Найти наибольшее и наименьшее значения функции на отрезке [ -3, 1]. Решение. Стационарные точки:
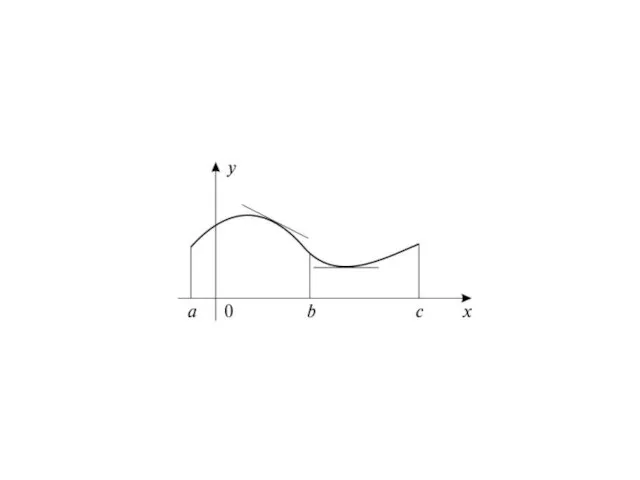
- 20. Выпуклость и вогнутость графика функции. Точки перегиба Кривая y=f(x) имеет на (a; b) выпуклость, направленную вверх,
- 22. Если функция y= f(x) имеет на интервале (a; b) вторую производную и на (a; b), то
- 23. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба. Необходимое условие перегиба в точке для
- 24. Достаточным условием перегиба является смена знака второй производной функции y=f(x) при переходе через точку (т.е.если вторая
- 25. Асимптоты Прямая линия называется асимптотой графика функции y = f(x), если расстояние от точки M, лежащей
- 26. Различают три вида асимптот: вертикальные, горизонтальные и наклонные . Прямая x=a называется вертикальной асимптотой графика функции
- 27. Прямая y=b называется горизонтальной асимптотой графика функции y=f(x) при если
- 28. Прямая называется наклонной асимптотой графика функции y=f(x) при если f(x) можно представить в виде где при
- 30. Пример. Найти наклонную асимптоту графика функции Решение. Уравнение наклонной асимптоты имеет вид:
- 32. Уравнение наклонной асимптоты:
- 33. Пример. Найти асимптоты графика функции Решение. x = 1 – вертикальная асимптота. Горизонтальных асимптот нет.
- 34. Найдем наклонную асимптоту:
- 35. – наклонная асимптота.
- 37. Скачать презентацию




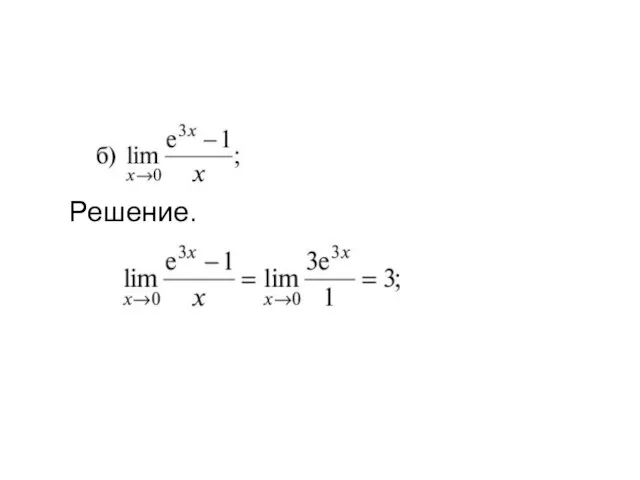
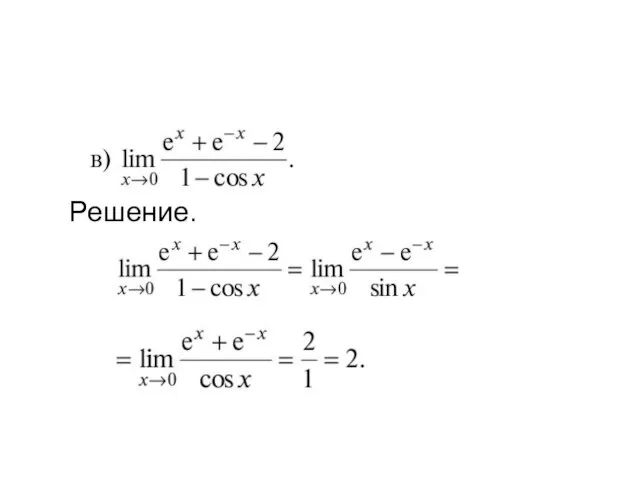










![Пример. Найти наибольшее и наименьшее значения функции на отрезке [ -3, 1]. Решение. Стационарные точки:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/367448/slide-17.jpg)
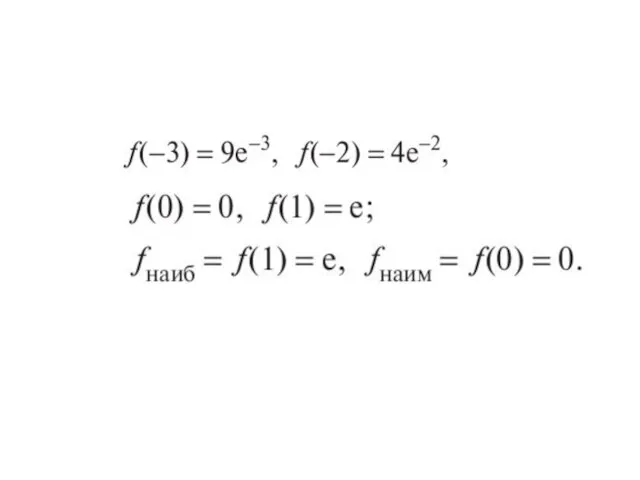








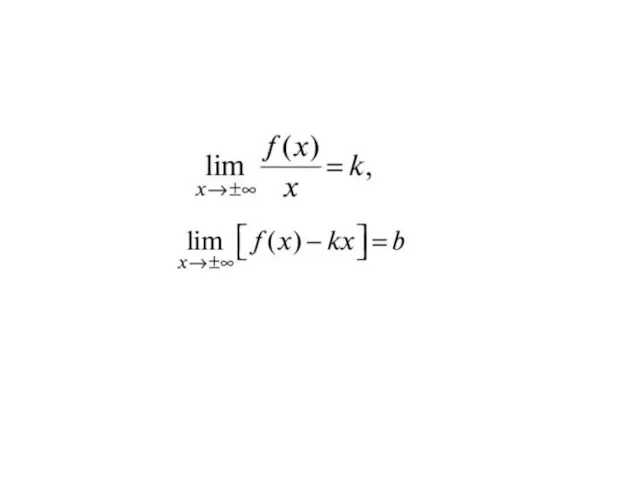

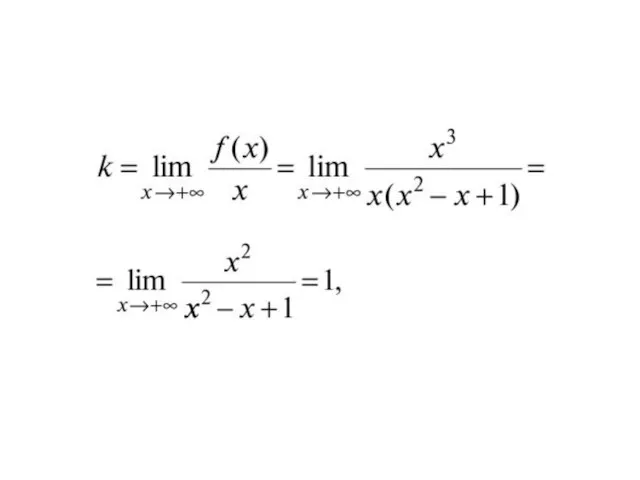




 Tesla
Tesla Оригами новогодняя ёлка
Оригами новогодняя ёлка Презентация на тему Решение задач по теме Колебания и волны
Презентация на тему Решение задач по теме Колебания и волны  Budowa roślin
Budowa roślin Презентация на тему Россия при Петре I
Презентация на тему Россия при Петре I  Пакетные предложения. Разработан для хоккея спроектирован для детей. Окно №2
Пакетные предложения. Разработан для хоккея спроектирован для детей. Окно №2 Презентация на тему Как сочинить волшебную сказку
Презентация на тему Как сочинить волшебную сказку  Развитие магистральных сетей: задачи энергостроительного комплекса
Развитие магистральных сетей: задачи энергостроительного комплекса Решение задач. Идеальный газ
Решение задач. Идеальный газ Непривычная динамика ценна рынке жилья:впервые за 20 летАналитический центр w w w . I R N . r u Март 2011 г.
Непривычная динамика ценна рынке жилья:впервые за 20 летАналитический центр w w w . I R N . r u Март 2011 г. o Центр корпоративного обучения « Оксфорд Класс » создан в 2007 г. в партнерстве с языковой школой Оксфорд Класс, г. Киев,Украина, год о
o Центр корпоративного обучения « Оксфорд Класс » создан в 2007 г. в партнерстве с языковой школой Оксфорд Класс, г. Киев,Украина, год о Скульптура АНТИЧНОСТИ
Скульптура АНТИЧНОСТИ Сервировка сладкого стола. Праздничный этикет
Сервировка сладкого стола. Праздничный этикет Чтобы зубы были здоровыми
Чтобы зубы были здоровыми Тема занятия: «Учет кассовых операций»
Тема занятия: «Учет кассовых операций» Требования к современному уроку
Требования к современному уроку Научно-методическое обеспечение деятельности школьных библиотекарей
Научно-методическое обеспечение деятельности школьных библиотекарей Муниципальное бюджетное общеобразовательное учреждение гимназия № 52 Октябрьского района города Росто
Муниципальное бюджетное общеобразовательное учреждение гимназия № 52 Октябрьского района города Росто России первая любовь
России первая любовь Графические интерфейсыпакет Tkinter
Графические интерфейсыпакет Tkinter Презентация на тему Мир
Презентация на тему Мир Операции с грузами по прибытию на станцию назначения
Операции с грузами по прибытию на станцию назначения Презентация на тему Познавательные процессы 8 класс
Презентация на тему Познавательные процессы 8 класс Русская народная музыка
Русская народная музыка Портрет первоклассника
Портрет первоклассника Организация структуры базы данных
Организация структуры базы данных Теория обучения в информационном обществе
Теория обучения в информационном обществе Особенности правового режима использования олимпийской и паралимпийской символики
Особенности правового режима использования олимпийской и паралимпийской символики