Содержание
- 2. Вопросы: Понятие системы счисления Позиционные и непозиционные системы счисления Алфавит и основание системы счисления
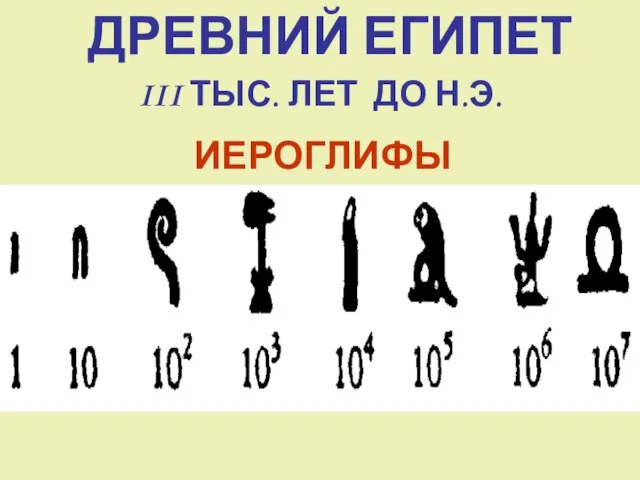
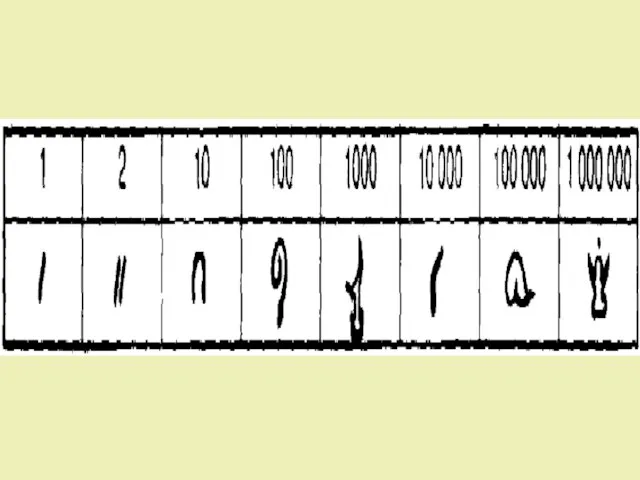
- 3. ДРЕВНИЙ ЕГИПЕТ III ТЫС. ЛЕТ ДО Н.Э. ИЕРОГЛИФЫ
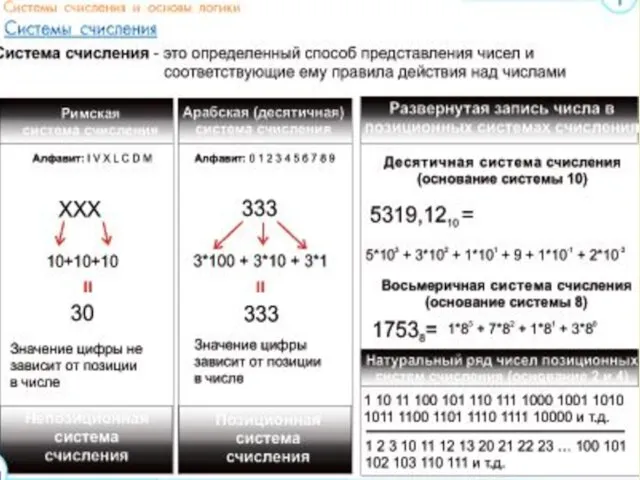
- 5. Система счисления – совокупность правил наименования и изображения чисел с помощью набора символов
- 6. 3252 = Величина числа, не зависит от положения (позиции) знака в записи числа
- 7. СИСТЕМА СЧИСЛЕНИЯ ДРЕВНЕГО ЕГИПТА - НЕПОЗИЦИОННАЯ
- 8. ДРЕВНИЙ РИМ 2,5 ТЫС. ЛЕТ НАЗАД
- 9. РИМСКИЕ ЦИФРЫ I - 1 V - 5 X – 10 L - 50 C -
- 10. I V X L C D M 1 5 10 50 100 500 1000 Centum –
- 11. В римских числах цифры записываются слева направо в порядке убывания. Если слева записана цифра меньшая, чем
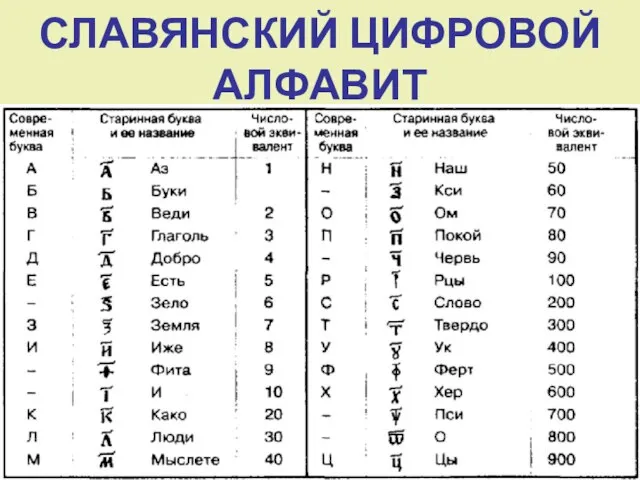
- 12. СЛАВЯНСКИЙ ЦИФРОВОЙ АЛФАВИТ
- 13. 1 =
- 14. ТЫСЯЧИ
- 15. « ТЬМА »
- 16. « ЛЕГИОНЫ »
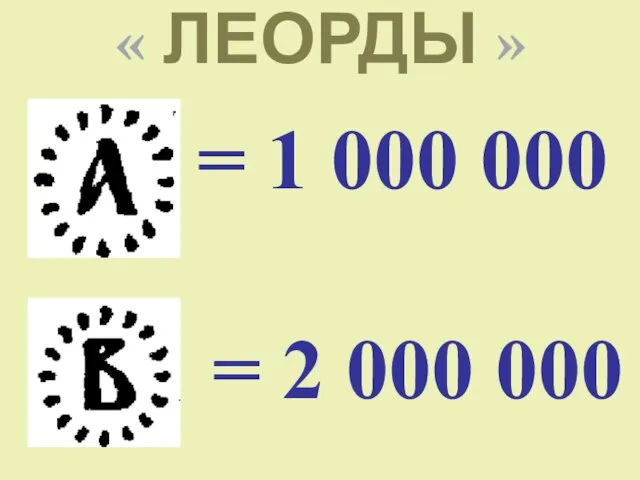
- 17. « ЛЕОРДЫ »
- 18. « ВОРОНА »
- 19. « КОЛОДА »
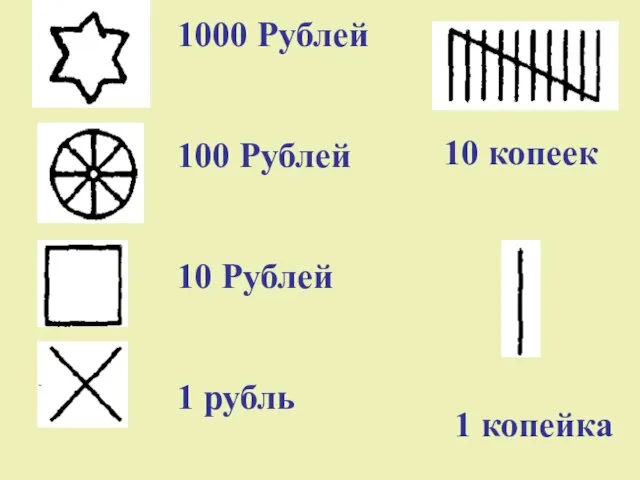
- 20. 1000 Рублей 100 Рублей 10 Рублей 1 рубль 10 копеек 1 копейка
- 21. 1232 рубля 24 копейки
- 22. ДРЕВНИЙ ВАВИЛОН III ТЫС. ЛЕТ ДО Н.Э. КЛИНОПИСЬ
- 23. СИСТЕМЫ СЧИСЛЕНИЯ ПОЗИЦИОННЫЕ НЕПОЗИЦИОННЫЕ римская десятичная двоичная восьмеричная 16 - ричная
- 24. ИНДИЯ V-VII B.B. ОСНОВАНИЕ 10-ЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ
- 25. АРАБСКИЕ ЦИФРЫ
- 26. ОДИН ИЗ ВАРИАНТОВ НАПИСАНИЯ ДЕСЯТИЧНЫХ ЦИФР В ЕВРОПЕ
- 27. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
- 28. Величина числа зависит от позиции цифры в числе 77710= 7*102 + 7*101 + 7*100 1012 =
- 29. АЛФАВИТ СИСТЕМЫ СЧИСЛЕНИЯ МНОЖЕСТВО (ЗНАКОВ) ЦИФР ИСПОЛЬЗУЕМЫХ В НЕЙ
- 30. ОСНОВАНИЕ СС - ЭТО КОЛИЧЕСТВО ЗНАКОВ, ИСПОЛЬЗУЕМЫХ ДЛЯ ИЗОБРАЖЕНИЯ ЦИФР В ДАННОЙ СИСТЕМЫ СЧИСЛЕНИЯ
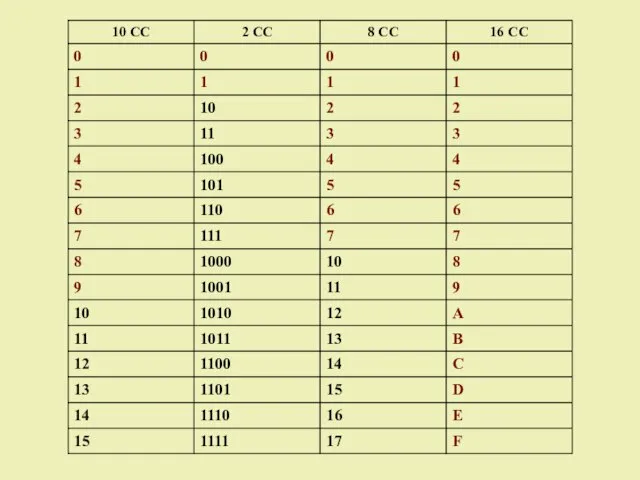
- 31. ДВОИЧНАЯ СИСТЕМА ОСНОВАНИЕ: 2 АЛФАВИТ: 0 , 1
- 32. ТРОИЧНАЯ СИСТЕМА ОСНОВАНИЕ: 3 АЛФАВИТ: 0 , 1 , 2
- 33. ВОСЬМЕРИЧНАЯ СИСТЕМА ОСНОВАНИЕ: 8 АЛФАВИТ: 0, 1 , 2, 3, 4, 5, 6, 7
- 34. ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМА ОСНОВАНИЕ: 16 АЛФАВИТ: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A,
- 36. ? Вопрос учащимся: Как изменятся числа 172,3410 и 101,112 при перенесении запятой вправо на один (два)
- 37. Базис Базис позиционной системы счисления – это последовательность чисел, каждое из которых задает значение цифры по
- 38. Пример. Выпишем базисы некоторых систем счисления. Десятичная система: …, 0,001, 0,01, 1, 10, 102, 103, 104,
- 39. Традиционные системы счисления. В более общем виде для традиционных позиционных систем счисления базис можно записать в
- 40. Знаменатель Р геометрической прогрессии, члены которой образуют базис традиционной системы счисления, называется основание системы счисления. Позиционные
- 41. Нетрадиционные системы: Пример базисов нетрадиционных систем: Факториальная система: 1!, 2!, 3!, 4!, …, (n-1)!, n!, …(основана
- 42. Применение двоичной системы счисления создает большие удобства для работы ЭВМ: для реализации двоичной системы счисления нужны
- 43. Недостатки двоичной системы счисления: Необходимость и трудоемкость перевода чисел из 10-ной СС при вводе информации и
- 44. Практическая работа «Ознакомление с различными системами счисления»
- 46. Подведем итоги: Вопросы: Почему, как вы думаете, для кодирования информации в компьютере используется двоичная система счисления?
- 48. Скачать презентацию








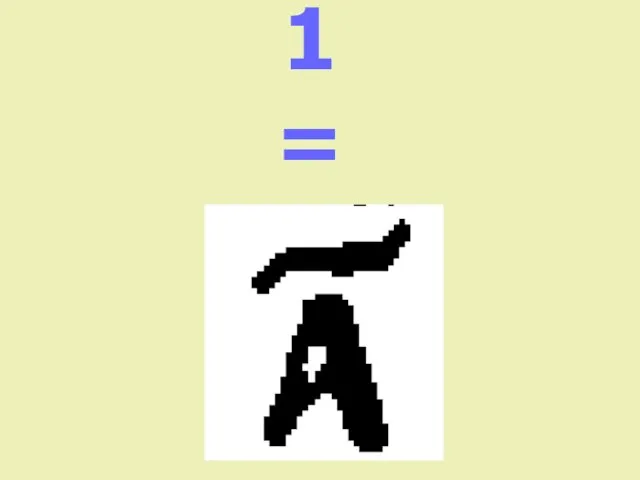





























 Отдельные виды договорных отношений в жилищном праве
Отдельные виды договорных отношений в жилищном праве Организация велостоянки для гимназии №1
Организация велостоянки для гимназии №1 О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го
О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го Урок русского языка в 6 классе по теме: «Правописание сложных существительных»
Урок русского языка в 6 классе по теме: «Правописание сложных существительных» Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании
Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании Невидимые нити в весеннем лесу (2 класс)
Невидимые нити в весеннем лесу (2 класс) Игрушки из носочков своими руками №7
Игрушки из носочков своими руками №7 Введение в специальность
Введение в специальность Герцог Ами
Герцог Ами Трение. Вредно или полезно
Трение. Вредно или полезно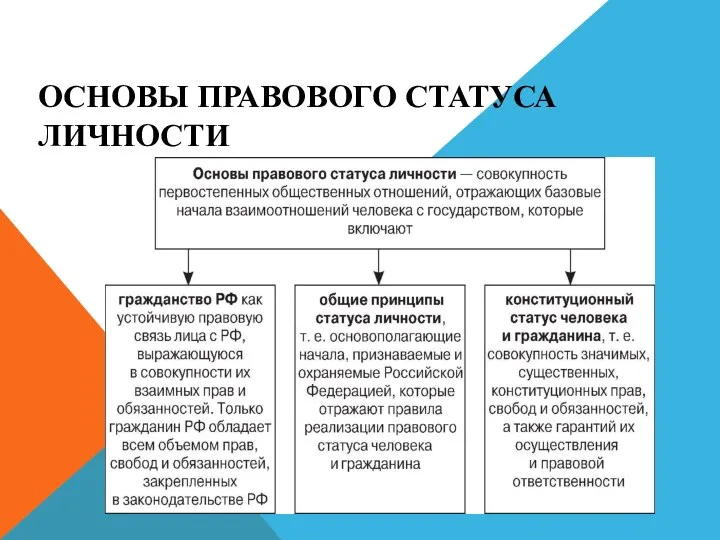 Правовой статус личности. Гражданство РФ
Правовой статус личности. Гражданство РФ Социальная психология
Социальная психология Презентация на тему АФАНАСИЙ НИКИТИН
Презентация на тему АФАНАСИЙ НИКИТИН  Теория обучения
Теория обучения Презентация на тему Our Environment (Наша окружающая среда)
Презентация на тему Our Environment (Наша окружающая среда) Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС)
Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС) Презентация по информатике на тему: «Устройства вывода информации, монитор.»
Презентация по информатике на тему: «Устройства вывода информации, монитор.» Круглопольское сельское поселение
Круглопольское сельское поселение Прайс косметологических услуг салона Забота о вас
Прайс косметологических услуг салона Забота о вас Патрон грязеуловителя
Патрон грязеуловителя Назначение изделия и его описание
Назначение изделия и его описание Планирование и организация процесса закупок материальных ресурсов промышленного предприятия
Планирование и организация процесса закупок материальных ресурсов промышленного предприятия Распространение объектно-ориентированного подхода на информационную безопасность
Распространение объектно-ориентированного подхода на информационную безопасность Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк.
Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк. Пейзаж в графике
Пейзаж в графике Рогожка. Коллекция однотонных штор
Рогожка. Коллекция однотонных штор _Презентация. Предоставление
_Презентация. Предоставление Презентация
Презентация