Содержание
- 2. Оқу мақсаттары: 11.3.1.4 - қисықсызықты трапецияның анықтамасын білу және оның ауданын табу үшін Ньютон-Лейбниц формуласын қолдану;
- 3. Сабақтың мақсаты: - анықталған интеграл анықтамасын біледі; - анықталған интеграл қасиеттерін қолданады; - анықталған интегралды Ньютон-Лейбниц
- 4. 1.Қисықсызықты трапецияның ауданы дегенімз не?
- 5. 1.Қисықсызықты трапеция [a;b] кесіндісі қисықсызықты трапецияның -табаны болады. Анықтама. Жоғарыдан үзіліссіз теріс емес y=f(x) функциясының графигімен,ал
- 6. 2.Ньютон-Лейбниц формуласы?
- 7. И.Ньютон 1643—1727 Г.Лейбниц 1646—1716 2.Ньютона-Лейбниц формуласы
- 8. 3.Алғашқы функциялардың формулаларын анықталған интегралды табуда қолданылады ма? Қандай түрлерін білесіздер?
- 10. 4. Қисықсызықты трапецияның ауданын есептеу алгоритмі қандай?
- 11. Қисықсызықты трапецияның ауданын есептеу алгоритмі. 1.Берілген сызықтарды координаталық жазықтықта салу; 2.Фигураны Ох осі бойымен шектелген кесіндінің
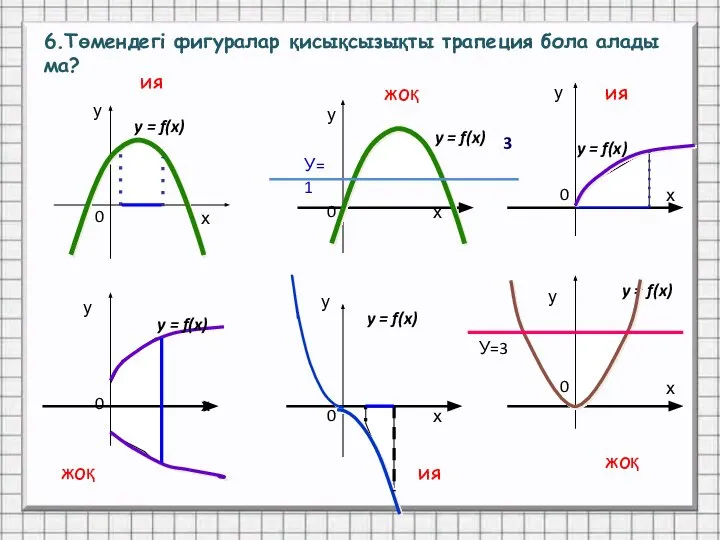
- 12. 5.Берілген фигуралар қисықсызықты трапеция бола ала ма?
- 13. у у у у у у У=1 3 y = f(x) y = f(x) y =
- 14. Миға шабуыл
- 15. Дескриптор. 1.Алғашқы функцияның жалпы түрін жаза алады. 2.Алғашқы функцияларды табу формулаларын қолданады. 3.Өрнектерді ықшамдай алады.
- 16. АНЫҚТАЛҒАН ИНТЕГРАЛДЫҢ КӨМЕГІМЕН ФИГУРАЛАРДЫҢ АУДАНЫН ЕСЕПТЕУ
- 17. Қисықсызықты трапецияның ауданын анықталған интеграл көмегімен есептеңіз
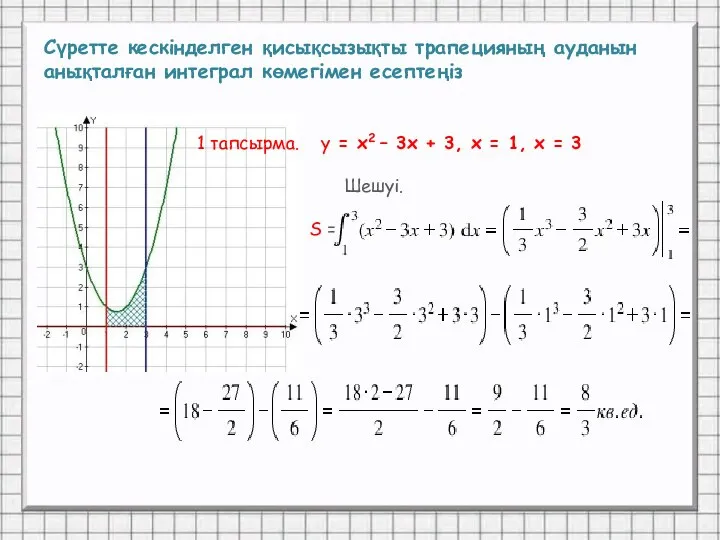
- 18. Сүретте кескінделген қисықсызықты трапецияның ауданын анықталған интеграл көмегімен есептеңіз 1 тапсырма. у = х2 – 3х
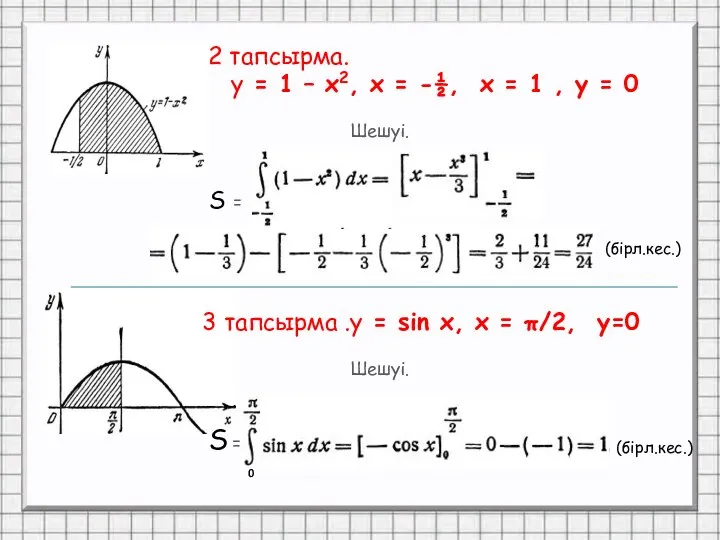
- 19. 2 тапсырма. у = 1 – х2, х = -½, х = 1 , у =
- 20. Дескриптор. 1.Қисықсызықты трапецияның ауданын таба алады; 2.Ньютон-Лейбниц формуланы жазық фигураның ауданын табуда қолданады; 3.Тригонометриялық функциялардың мәндерін
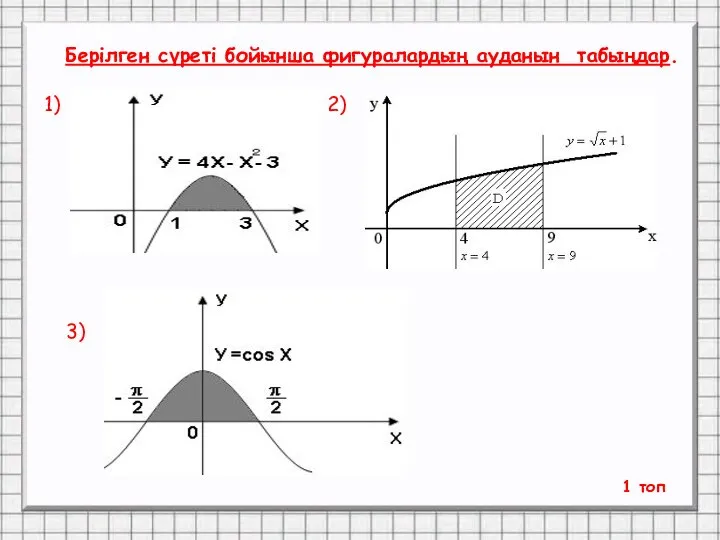
- 21. Берілген сүреті бойынша фигуралардың ауданын табыңдар. 1) 2) 1 топ 3)
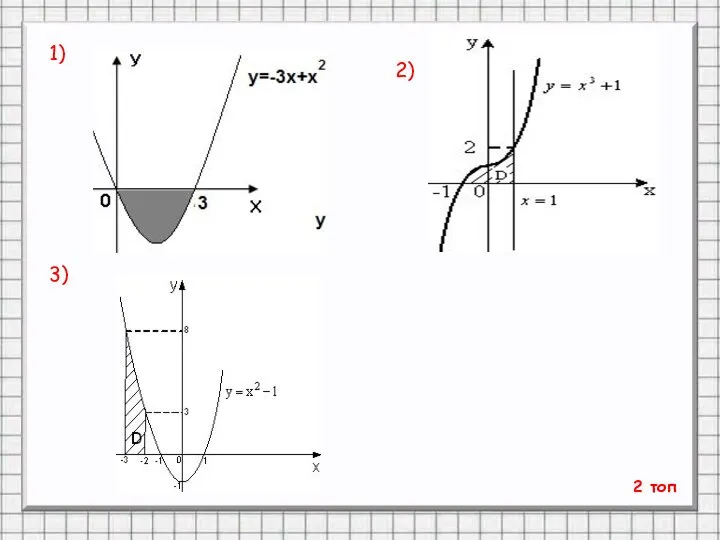
- 22. 1) 2) 3) 2 топ
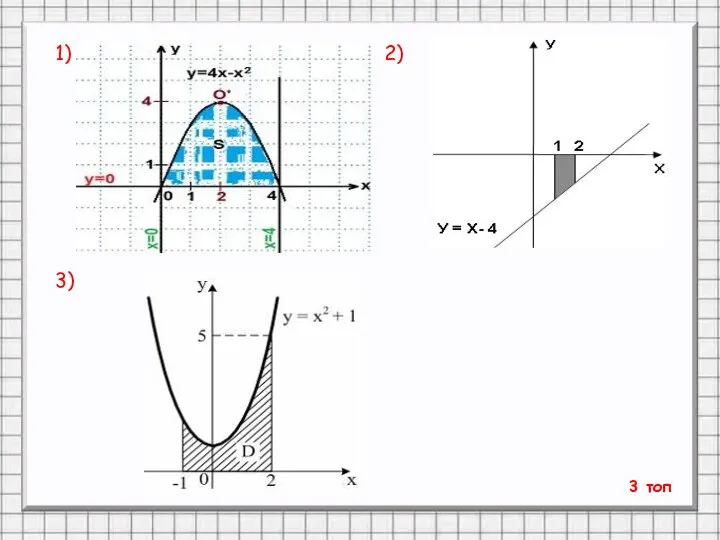
- 23. 3 топ 1) 2) 3)
- 24. Деңгейлік тапсырмалар.
- 25. Дескриптор Қисықсызықты трапецияның ауданын есептеу алгоритмін біледі; Квадрат теңдеулердің түбірін таба алады; Арифметикалық квадрат түбірдің анықтамасын
- 26. Жауаптары
- 28. Скачать презентацию



![1.Қисықсызықты трапеция [a;b] кесіндісі қисықсызықты трапецияның -табаны болады. Анықтама. Жоғарыдан үзіліссіз теріс](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1181078/slide-4.jpg)















 Алтайские горы
Алтайские горы Я тебя люблю
Я тебя люблю От чтения к скорочтению
От чтения к скорочтению HOW YOU BEGIN YOUR PRESENTATION
HOW YOU BEGIN YOUR PRESENTATION Sport In Great Britain
Sport In Great Britain Презентация на тему Древние германцы и Римская империя
Презентация на тему Древние германцы и Римская империя  Отношения «больше» и «меньше»
Отношения «больше» и «меньше» Гюстав Моро. Жизнь и творчество
Гюстав Моро. Жизнь и творчество Истоки педагогической теории в Древней Греции
Истоки педагогической теории в Древней Греции Три закона Ньютона
Три закона Ньютона Ягодное яссорти
Ягодное яссорти казки народів світу
казки народів світу Лекция 2. Наследственность и среда
Лекция 2. Наследственность и среда Опасные и чрезвычайные ситуации
Опасные и чрезвычайные ситуации Сатанизм
Сатанизм Муниципальное общеобразовательное учреждение«Гимназия №1» г. Белгорода
Муниципальное общеобразовательное учреждение«Гимназия №1» г. Белгорода Психологическое насилие в образовательной среде и причины его возникновения
Психологическое насилие в образовательной среде и причины его возникновения Информационные процессы
Информационные процессы Основы брендинга. Экзаменационное задание
Основы брендинга. Экзаменационное задание Медиа проект по теме: Служба в Вооружённых Силах - мой долг перед Отечеством
Медиа проект по теме: Служба в Вооружённых Силах - мой долг перед Отечеством От кого же, мы всё же произошли?
От кого же, мы всё же произошли? Проблемы урегулирования межорганизационных конфликтов в предпринимательских сетях
Проблемы урегулирования межорганизационных конфликтов в предпринимательских сетях Музейный Дом
Музейный Дом Презентация на тему Саратовская область
Презентация на тему Саратовская область Akimov (KAZAN, 06.10.2022)
Akimov (KAZAN, 06.10.2022) Презентация на тему Фосфорная кислота и ее свойства
Презентация на тему Фосфорная кислота и ее свойства Лесной комплекс России
Лесной комплекс России TresEvent. Философия
TresEvent. Философия