К фильтрационным параметрам относятся

В основе определения фильтрационных параметров лежит решение уравнений водопритока к скважинам относительно переменных, характеризующих свойства водовмещающих пород (обратная задача).
Опытно-фильтрационные работы

Нестационарный (неустановившийся)
уравнение Тейса:
Квазистационарный (квазиустановившийся)
уравнение Тейса-Джейкоба:
Стационарный (установившийся)
уравнение Дюпюи:
Уравнения водопритока к скважинам
Ржимы водопритока

Метод временного прослеживания уровня
Наиболее точно можно определить фильтрационные параметры по данным длительных кустовых откачек, описываемых уравнением Тейса-Джейкоба:
Опытно-фильтрационные работы

Необходимость использования кустовых откачек (с наблюдательными скважинами) связана с тем, что в центральной скважине куста при откачке возникает гидравлический скачок уровня, вызывающий несовпадение уровня в скважине и в водоносном горизонте, и не позволяющий замерить истинную величину понижения.
В наблюдательных скважинах (скважине) отсутствует водоотбор и гидравлический скачок уровня не возникает.
Опытно-фильтрационные работы

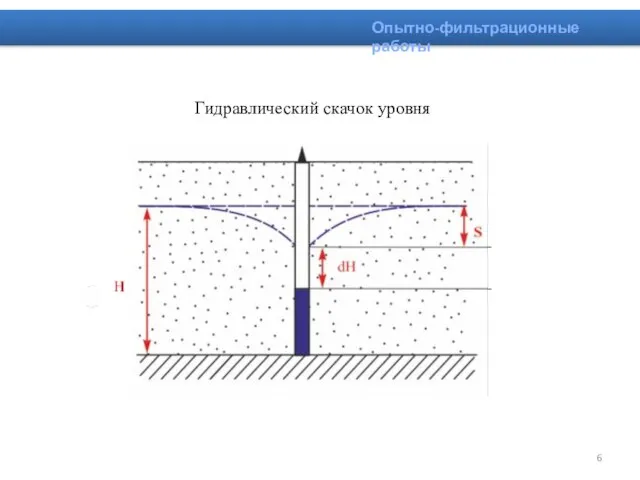
Гидравлический скачок уровня
Опытно-фильтрационные работы

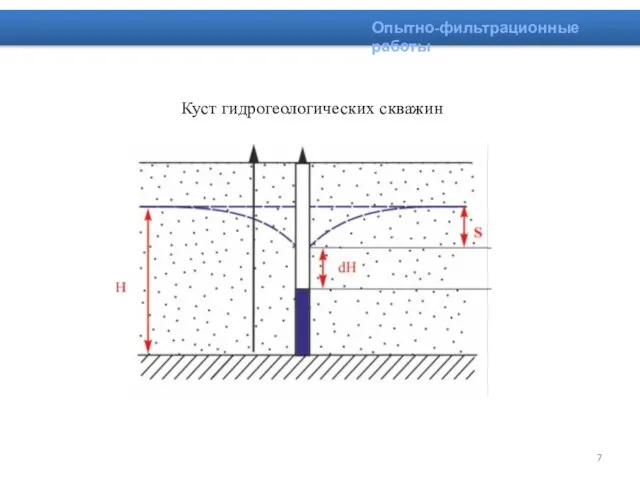
Куст гидрогеологических скважин
Опытно-фильтрационные работы

Решение одного уравнения с двумя неизвестными невозможно, поэтому для получения решения используют дополнительные приёмы обработки.
Графоаналитические методы прямолинейной анаморфозы построены на преобразовании исходных зависимостей к прямолинейному виду и графоаналитическому определению параметров прямолинейных частей графиков, построенных на основе опытных данных:
Опытно-фильтрационные работы
Уравнение Тейса-Джейкоба является уравнением прямой линии вида:

Опытно-фильтрационные работы
km – const;
a – const;
r – const;
t – независимая переменная;
Q – const (техническое требование к проведению откачки);
Метод временного прослеживания уровня
Уравнение Тейса-Джейкоба:

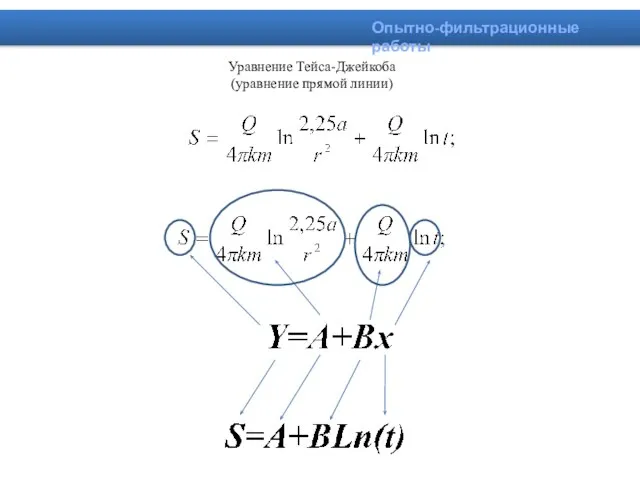
Уравнение Тейса-Джейкоба
(уравнение прямой линии)
Опытно-фильтрационные работы

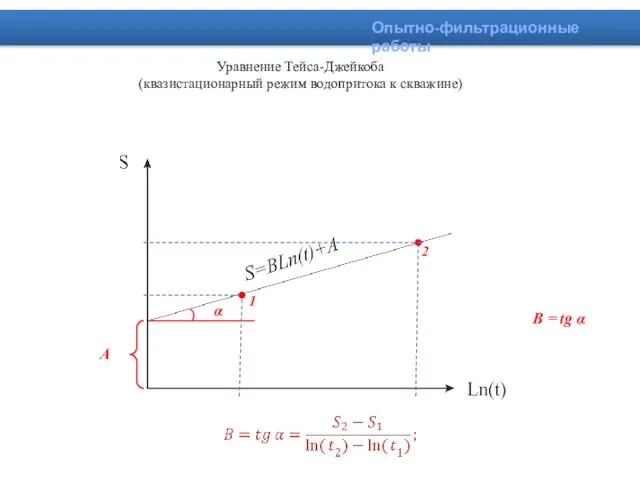
Уравнение Тейса-Джейкоба
(квазистационарный режим водопритока к скважине)
Опытно-фильтрационные работы
1
2

Уравнение Тейса-Джейкоба
(квазистационарный режим водопритока к скважине)
Опытно-фильтрационные работы

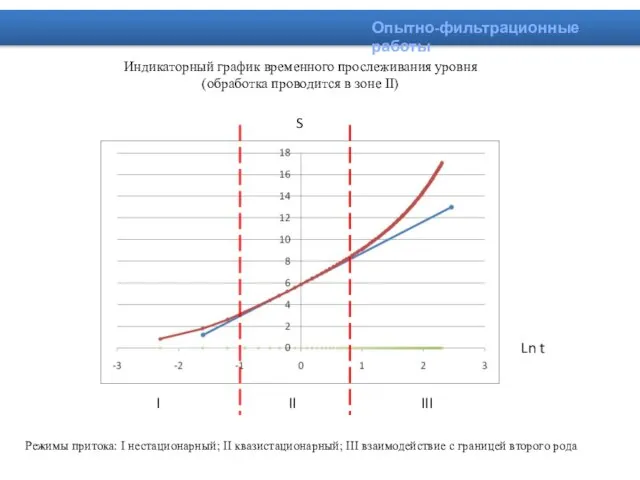
Индикаторный график временного прослеживания уровня
(обработка проводится в зоне II)
S
Ln t
I
II
III
Режимы притока: I нестационарный; II квазистационарный; III взаимодействие с границей второго рода
Опытно-фильтрационные работы