Капиллярно-волновая модель межфазных границ: итоги и перспективы исследований

Граница пар―жидкость:
плавный переход или слоистая структура?
Газ
Жидкость
Газ
Жидкость
Промежуточная фаза

Методы исследования:
1. аналитические;
2. экспериментальные (отражение
рентгеновского излучения и нейтронов); 3. численный эксперимент (молекулярная
динамика + Монте-Карло).

Трудности капиллярно-волновой модели:
Что такое микроскопическая волновая поверхность? Как рассматривать «гребешки» волн?
Как отделить капиллярные флуктуации от объемных?
Какое поверхностное натяжение адекватно микрокапиллярным флуктуациям?

Частицы делятся на три типа. Частицу 1 с радиус-вектором назовем внутренней, если существует по крайней мере одна частица 2 с числом связей более четырех и координатой такой, что выполняются условия
где – число частиц кластера в единице объема. Частицы, не являющиеся внутренними и имеющие более четырех ближайших соседей, будем называть поверхностными, а частицы с числом связей менее пяти отнесем к виртуальным цепям.
Положение №1: разделить частицы, являющиеся «опорными» для волновой (флуктуационной) поверхности и виртуальные цепи (частицы, слабо связанные с кластером). Как следствие, ограничивается максимальная кривизна волновой поверхности.

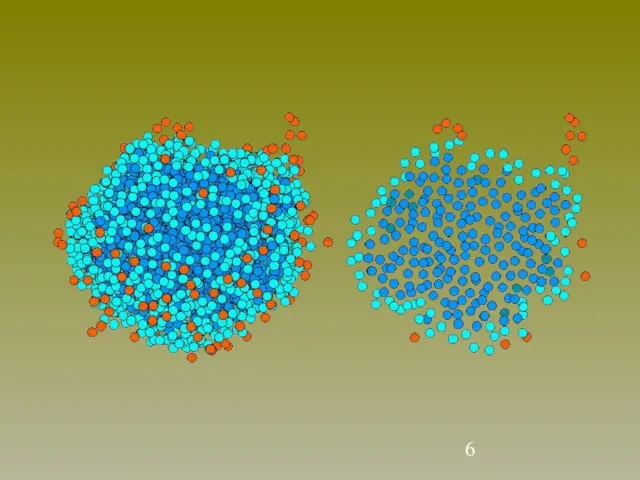
Поперечные сечения кластеров, содержащих 1592 (1) и 2320 (2) частиц. Темные кружки ― внутренние частицы, заштрихованные ― поверхностные, светлые ― виртуальные цепи. Поверхностные частицы формируют монослой, сильно искривленный тепловыми флуктуациями. Для внутренних частиц число связей не менее 10, а частицы, имеющие не более четырех связей, образуют виртуальные цепи.

Выделим поверхностные частицы, расположенные между двумя параллельными плоскостями. Полярные координаты частиц ― это значения непрерывной функции
Спектральные амплитуды сечений определялись усреднением как по конфигурациям кластера, так и по углам Эйлера при вращении каждой конфигурации:

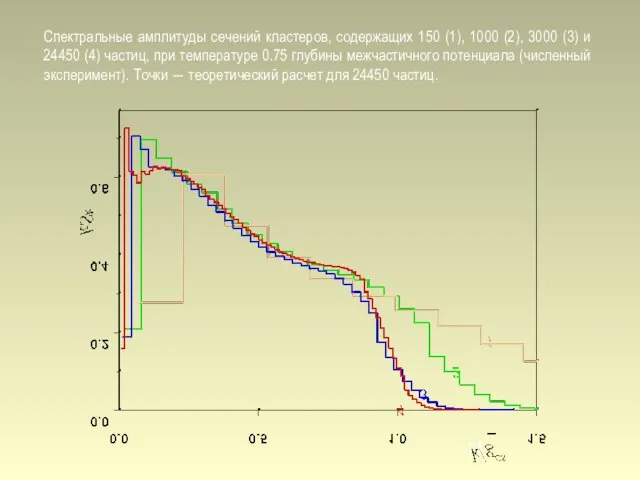
Спектральные амплитуды сечений кластеров, содержащих 150 (1), 1000 (2), 3000 (3) и 24450 (4) частиц, при температуре 0.75 глубины межчастичного потенциала (численный эксперимент). Точки ― теоретический расчет для 24450 частиц.

Положение №2: Объемные флуктуации обусловлены случайным расположением поверхностных частиц в пространстве. Они, следовательно, моделируются флуктуациям поверхностных частиц кластера, усеченного сферой. Полная спектральная плотность

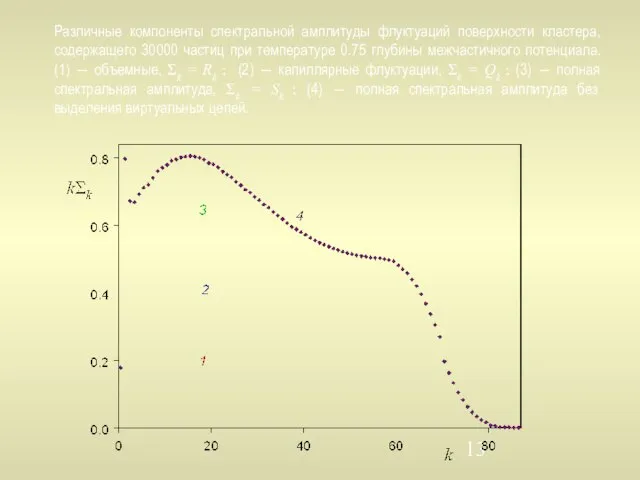
Различные компоненты спектральной амплитуды флуктуаций поверхности кластера, содержащего 30000 частиц при температуре 0.75 глубины межчастичного потенциала. (1) ― объемные, Σk = Rk ; (2) ― капиллярные флуктуации, Σk = Qk ; (3) ― полная спектральная амплитуда, Σk = Sk ; (4) ― полная спектральная амплитуда без выделения виртуальных цепей.

Теория капиллярных флуктуаций
В пионерской работе (Buff, Lovett, Stillinger, 1965) было получено соотношение
Попытки учесть зависимость поверхностного натяжения для флуктуаций от волнового числа приводит в противоречивым результатам, например к возрастающей (Helfrich, 1973)
убывающей зависимости (Mecke, 1999) и к более сложным зависимостям.
где ― константа связи.
где ― жесткость на изгиб для поверхности,

где
Согласно теории флуктуаций, изменение свободной энергии Гиббса поверхности кластера есть
где
С помощью теоремы о равнораспределении получим
Условие конечности избыточной поверхности кластера

где
позволяет найти максимальное значение l
и связь между константой связи и обычным поверхностным натяжением :
Здесь
― универсальная постоянная.

где
Капиллярная флуктуация в форме сферической гармоники Ylm
где ― амплитуда, соответствующая , дает вклад в наблюдаемый в численном эксперименте двумерный спектр
Он определяется коэффициентами Фурье-разложения границы сечения
Тогда полная спектральная амплитуда капиллярных флуктуаций

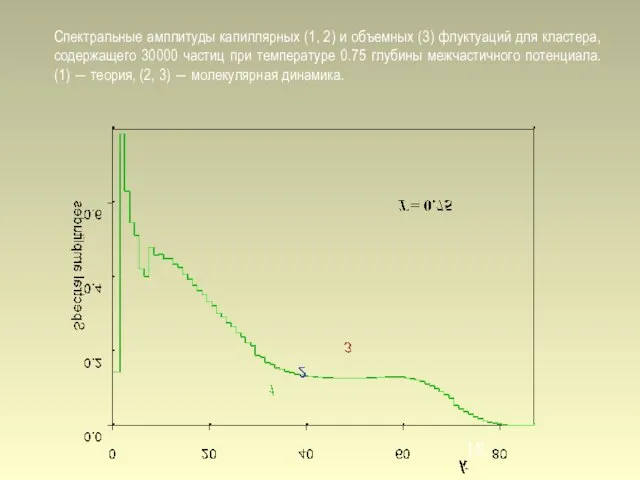
Спектральные амплитуды капиллярных (1, 2) и объемных (3) флуктуаций для кластера, содержащего 30000 частиц при температуре 0.75 глубины межчастичного потенциала. (1) ― теория, (2, 3) ― молекулярная динамика.

где
Эффективное поверхностное натяжение определяется как
где не зависит от m. В «классической» теории . Полная спектральная амплитуда капиллярных флуктуаций
Рассматривалась двухпараметрическая
(Θ – функция Хевисайда) и трехпараметрическая
зависимости. Параметры выбирались из условия наилучшего описания МД:

где

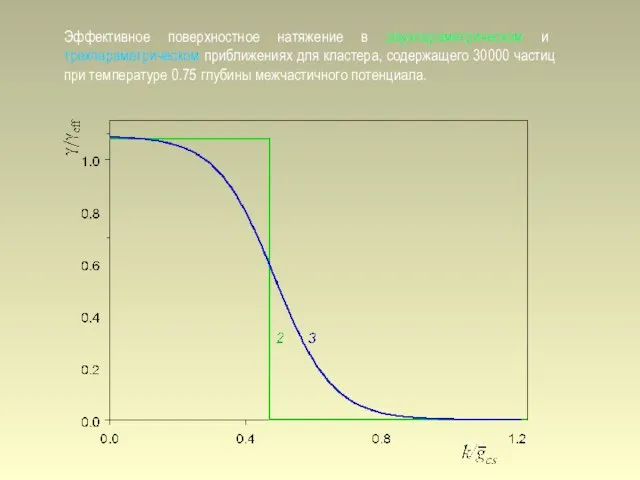
Эффективное поверхностное натяжение в двухпараметрическом и трехпараметрическом приближениях для кластера, содержащего 30000 частиц при температуре 0.75 глубины межчастичного потенциала.

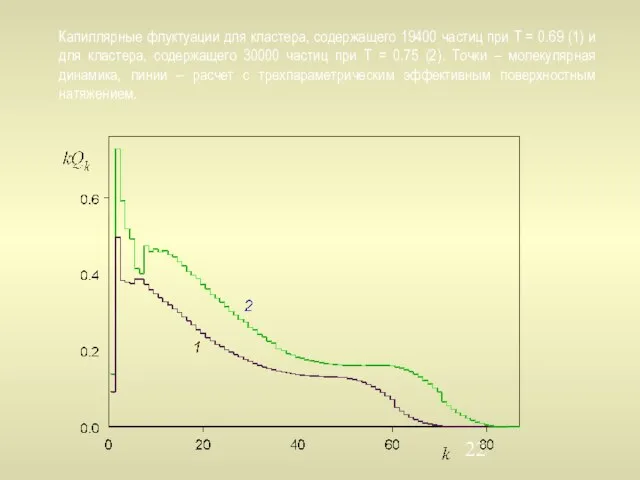
Капиллярные флуктуации для кластера, содержащего 19400 частиц при T = 0.69 (1) и для кластера, содержащего 30000 частиц при T = 0.75 (2). Точки – молекулярная динамика, линии – расчет с трехпараметрическим эффективным поверхностным натяжением.

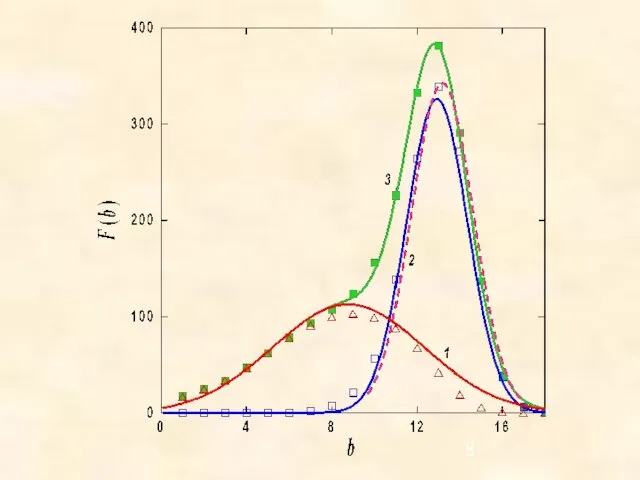
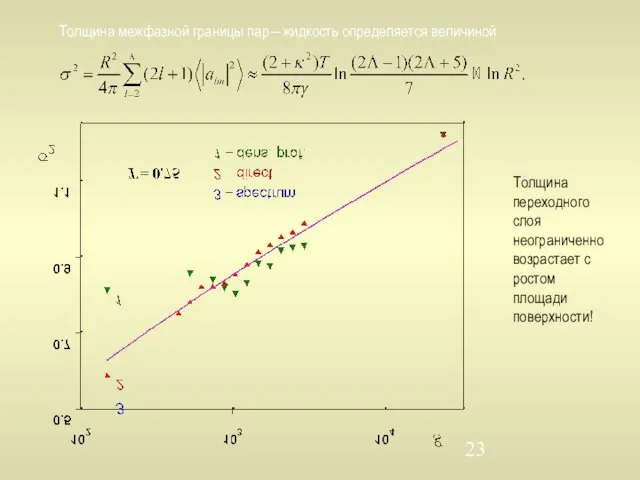
Толщина межфазной границы пар―жидкость определяется величиной
Толщина переходного слоя неограниченно возрастает с ростом площади поверхности!

< >
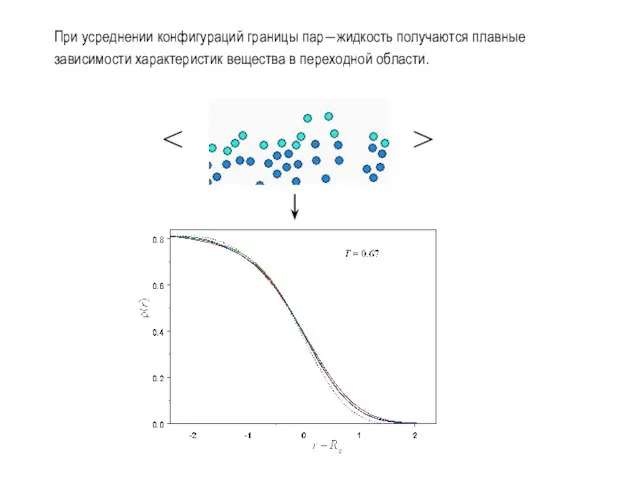
При усреднении конфигураций границы пар―жидкость получаются плавные зависимости характеристик вещества в переходной области.

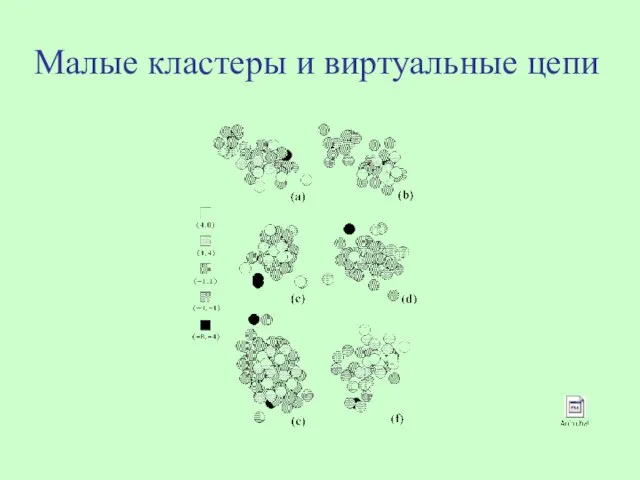
Малые кластеры и виртуальные цепи

Малые кластеры, характеризуемые минимальным числом связей, образуют виртуальные цепи. Их статсумма вычисляется аналитически:
откуда следует, например, уравнение состояния кластерного пара

Направления исследований
Капиллярные флуктуации и виртуальные цепи при приближении к критической точке.
Капиллярные флуктуации на поверхности жидкого металла.
Поверхность жидкого металла при приближении к критической точке.
Капиллярные флуктуации в сильных полях.
Межфазная граница при большом градиенте температуры.