КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ

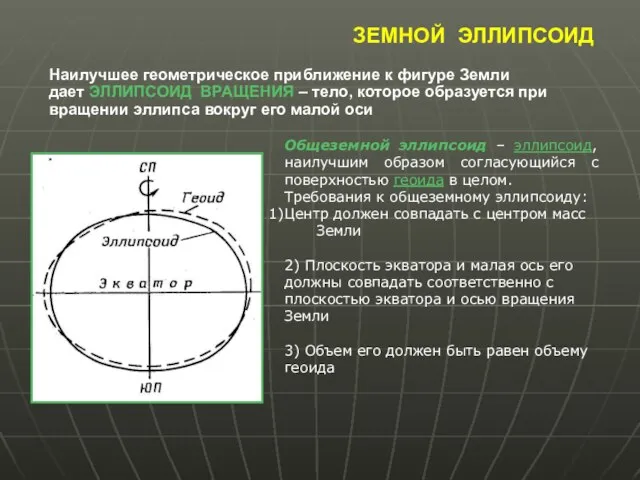
ЗЕМНОЙ ЭЛЛИПСОИД
Наилучшее геометрическое приближение к фигуре Земли
дает ЭЛЛИПСОИД ВРАЩЕНИЯ – тело, которое образуется при
вращении эллипса вокруг его малой оси
Общеземной эллипсоид – эллипсоид, наилучшим образом согласующийся с поверхностью геоида в целом.
Требования к общеземному эллипсоиду:
Центр должен совпадать с центром масс Земли
2) Плоскость экватора и малая ось его должны совпадать соответственно с плоскостью экватора и осью вращения Земли
3) Объем его должен быть равен объему геоида

ЗЕМНОЙ ЭЛЛИПСОИД
Земной эллипсоид имеет три основных параметра, любые два из которых однозначно определяют его фигуру:
большая полуось (экваториальный радиус) эллипсоида, a;
малая полуось (полярный радиус), b;
геометрическое (полярное) сжатие f=(a-b)/a.

ОБЩЕЗЕМНЫЕ ЭЛЛИПСОИДЫ
Современные общеземные эллипсоиды:
GRS80 (Geodetic Reference System 1980) разработан Международной Ассоциацией Геодезии и Геофизики (International Union of Geodesy and Geophysics) и рекомендован для геодезических работ;
WGS84WGS84 (World Geodetic System 1984) применяется в системе спутниковой навигации GPS;
ПЗ-90ПЗ-90 (Параметры Земли 1990 года) используется на территории России для геодезического обеспечения орбитальных полетов. Этот эллипсоид применяется в системе спутниковой навигации ГЛОНАСС;
IERS96IERS96 (International Earth Rotation Service 1996) рекомендован Международной службой вращения ЗемлиIERS96 (International Earth Rotation Service 1996) рекомендован Международной службой вращения Земли для обработки РСДБ-наблюдений.

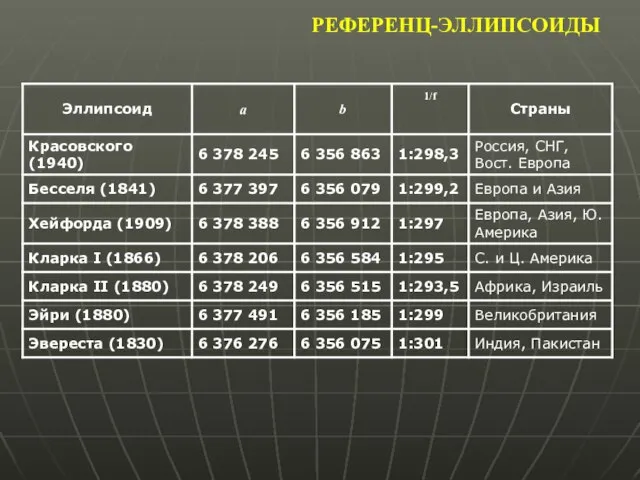
РЕФЕРЕНЦ-ЭЛЛИПСОИДЫ
Референц-эллипсоид (от лат. referens – сообщающий, вспомогательный) – наилучшим образом согласуется с поверхностью геоида на ограниченной части его поверхности.
Ориентирование референц-эллипсоида в теле Земли подчиняется следующим требованиям:
Малая полуось эллипсоида (b) должна быть параллельна оси вращения Земли;
- Поверхность эллипсоида должна находиться возможно ближе к поверхности геоида в пределах данного региона.

РЕФЕРЕНЦ-ЭЛЛИПСОИДЫ

КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ
КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ – ЭТО МАТЕМАТИЧЕСКИ ОПРЕДЕЛЕННОЕ ОТОБРАЖЕНИЕ ПОВЕРХНОСТИ ЭЛЛИПСОИДА ИЛИ ШАРА НА ПЛОСКОСТИ
Уравнения проекции в общем виде:
Х = f1(B, L); Y = f2(B, L)
B –широта, L – долгота
Х и Y – прямоугольные координаты
Z
Y
X
O
B
L

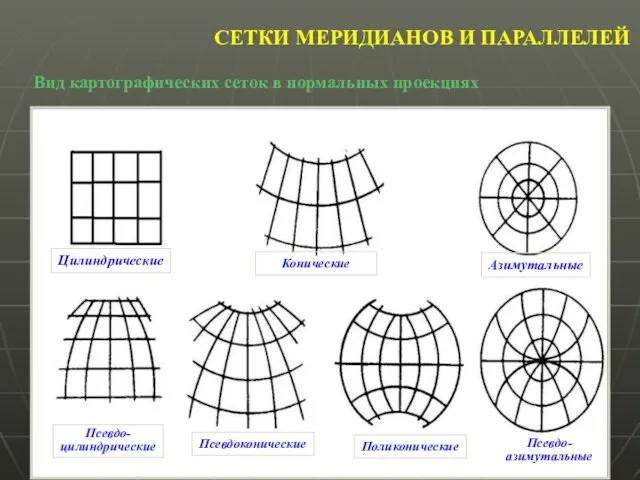
СЕТКИ КООРДИНАТ
В зависимости от положения оси системы сферических координат, используемой при проецировании, различаются:
Нормальная система – ось сферических координат совпадает с осью вращения Земли
Поперечная система – ось сферических координат лежит в плоскости экватора
Косая система – ось сферических координат расположена под углом к оси вращения Земли

СЕТКИ МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ
Вид картографических сеток в нормальных проекциях

КЛАССИФИКАЦИЯ ПРОЕКЦИЙ
Цилиндрические
Конические
Азимутальные
Псевдоцилиндрические
Псевдоконические
Псевдоазимутальные
Поликонические
Многогранные
Многополосные
Условные
Классификация по виду
нормальной картографической сетки

КЛАССИФИКАЦИЯ ПРОЕКЦИЙ
Равновеликие
Равноугольные
Произвольные, в том числе
Равнопромежуточные
- по меридианам
- по параллелям
Классификация
по характеру искажений

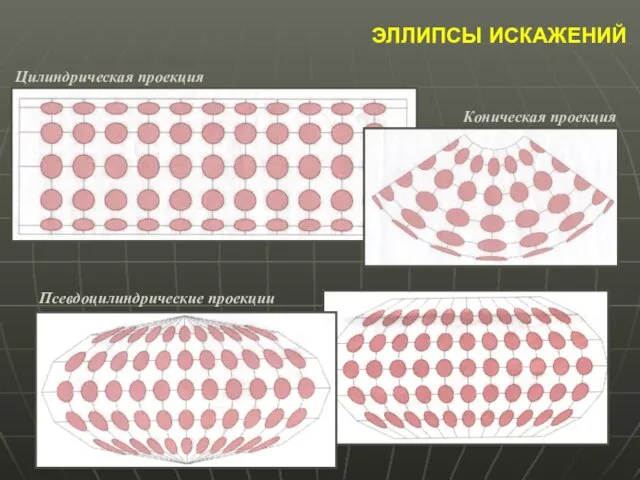
ЭЛЛИПС ИСКАЖЕНИЙ
Эллипс искажений
или индикатриса Тиссо –
характеризует искажения
масштабов в данной точке (в центре эллипса)
а – направление наибольшего растяжения масштаба
b – направление наибольшего сжатия масштаба
m – масштаб по меридиану
n – масштаб по параллели
Виды искажений в проекциях:
Искажения длин (a и b)
Искажения площадей (р= m n Sinθ)
Искажения углов и форм (ω)
Искажения определяют:
аналитически
по номограммам
по картам с изоколами –
изолиниями искажений

Главный масштаб – масштаб на линиях и в точках нулевых искажений;
Частный масштаб – масштаб в отдельно взятой точке;
Средний (осредненный) масштаб – величина приблизительного уменьшения территории для отображения на карте.

ЭЛЛИПСЫ ИСКАЖЕНИЙ