МАТЕМАТИЧЕСКАЯ ОСНОВА КАРТ

КАРТА
carte – французский
Karte – немецкий
map, сhart – английский
kort – датский
carta – итальянский, португальский
kaart – голландский
terkep – венгерский
zemelapis – литовский
tizu – японский
mapa – польский, чешский, словацкий, испанский
мапа, карта – украинский
от латинского “Charta” – лист, бумага
от греческого “χαρτηζ” – бумага из папируса
Карта – чертеж какой-либо части земли, моря, тверди небесной (В.Даль, Толковый словарь, 1881 г.)

КАРТА – это математически определенное, уменьшенное, генерализованное изображение поверхности Земли, другого небесного тела или космического пространства, показывающее расположенные или спроецированные на них объекты и их свойства в принятой системе условных знаков
ОПРЕДЕЛЕНИЕ

Математический закон построения – применение проекций и масштаба
Знаковость изображения – особый условный язык картографических знаков
Генерализованность – отбор и обобщение изображаемых объектов
Системность изображения – показ элементов, связей между ними, иерархии геосистем
СВОЙСТВА КАРТЫ

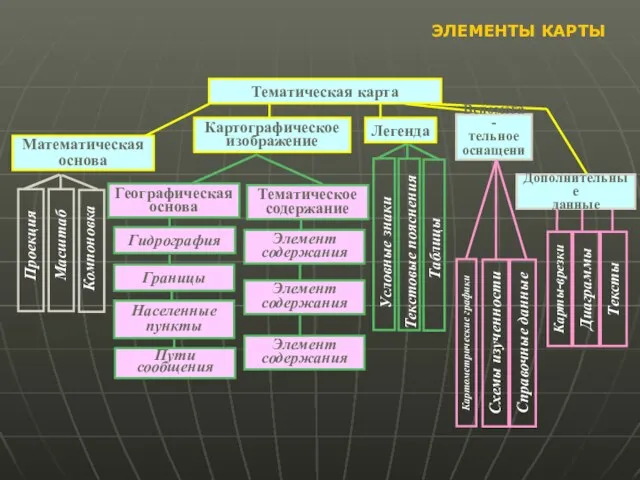
Тематическая карта
Математическая
основа
Вспомога-
тельное
оснащение
Дополнительные
данные
Карты-врезки
Диаграммы
Тексты
Картометрические графики
Схемы изученности
Справочные данные
ЭЛЕМЕНТЫ КАРТЫ
Картографическое
изображение
Легенда
Населенные пункты

ФИГУРА ЗЕМЛИ
вычислено по данным гравиметрической съемки Eigen-cg01, Германия
ГЕОИД - геометрическая фигура, которая совпадает со средней поверхностью вод Мирового океана, свободной от приливов, течений и прочих возмущений

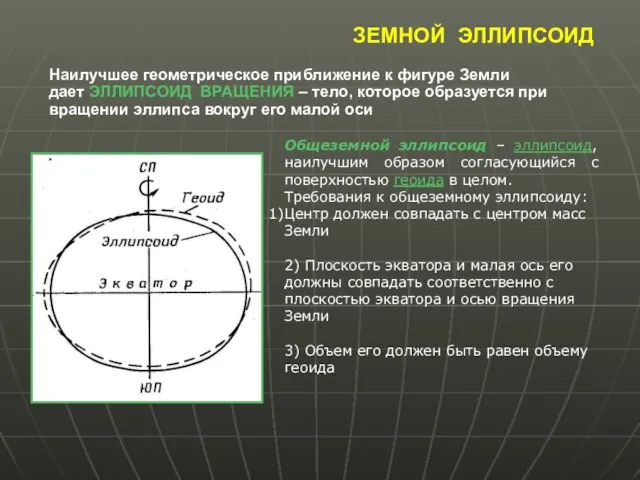
ЗЕМНОЙ ЭЛЛИПСОИД
Наилучшее геометрическое приближение к фигуре Земли
дает ЭЛЛИПСОИД ВРАЩЕНИЯ – тело, которое образуется при
вращении эллипса вокруг его малой оси
Общеземной эллипсоид – эллипсоид, наилучшим образом согласующийся с поверхностью геоида в целом.
Требования к общеземному эллипсоиду:
Центр должен совпадать с центром масс Земли
2) Плоскость экватора и малая ось его должны совпадать соответственно с плоскостью экватора и осью вращения Земли
3) Объем его должен быть равен объему геоида

ЗЕМНОЙ ЭЛЛИПСОИД
Земной эллипсоид имеет три основных параметра, любые два из которых однозначно определяют его фигуру:
большая полуось (экваториальный радиус) эллипсоида, a;
малая полуось (полярный радиус), b;
геометрическое (полярное) сжатие f=(a-b)/a.

ЗЕМНОЙ ЭЛЛИПСОИД
Современные общеземные эллипсоиды:
GRS80 (Geodetic Reference System 1980) разработан Международной Ассоциацией Геодезии и Геофизики (International Union of Geodesy and Geophysics) и рекомендован для геодезических работ;
WGS84WGS84 (World Geodetic System 1984) применяется в системе спутниковой навигации GPS;
ПЗ-90ПЗ-90 (Параметры Земли 1990 года) используется на территории России для геодезического обеспечения орбитальных полетов. Этот эллипсоид применяется в системе спутниковой навигации ГЛОНАСС;
IERS96IERS96 (International Earth Rotation Service 1996) рекомендован Международной службой вращения ЗемлиIERS96 (International Earth Rotation Service 1996) рекомендован Международной службой вращения Земли для обработки РСДБ-наблюдений.

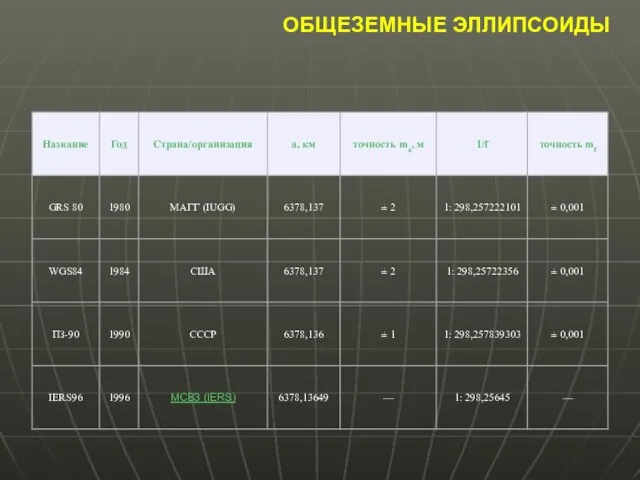
ОБЩЕЗЕМНЫЕ ЭЛЛИПСОИДЫ

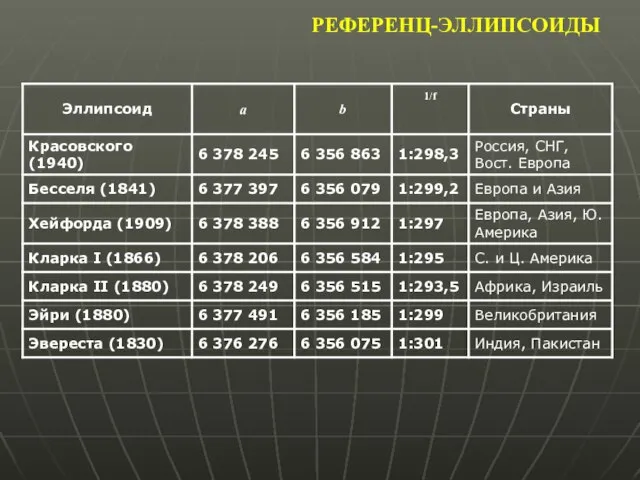
РЕФЕРЕНЦ-ЭЛЛИПСОИДЫ
Референц-эллипсоид (от лат. referens – сообщающий, вспомогательный) – наилучшим образом согласуется с поверхностью геоида на ограниченной части его поверхности.
Ориентирование референц-эллипсоида в теле Земли подчиняется следующим требованиям:
Малая полуось эллипсоида (b) должна быть параллельна оси вращения Земли;
- Поверхность эллипсоида должна находиться возможно ближе к поверхности геоида в пределах данного региона.

РЕФЕРЕНЦ-ЭЛЛИПСОИДЫ

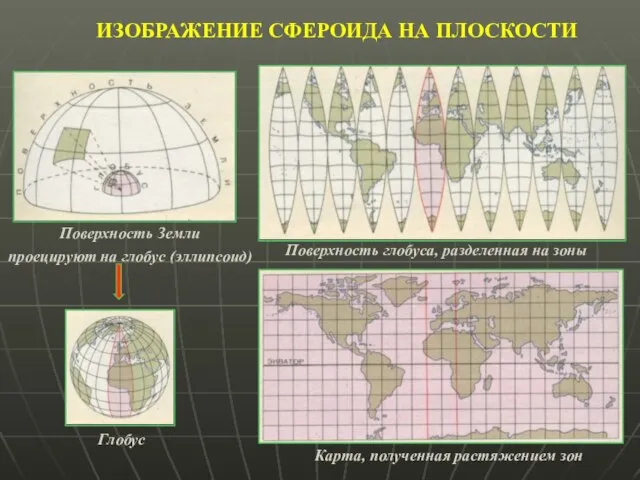
ИЗОБРАЖЕНИЕ СФЕРОИДА НА ПЛОСКОСТИ
Поверхность Земли
проецируют на глобус (эллипсоид)
Глобус
Поверхность глобуса, разделенная на зоны
Карта, полученная растяжением зон

КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ
КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ – ЭТО МАТЕМАТИЧЕСКИ ОПРЕДЕЛЕННОЕ ОТОБРАЖЕНИЕ ПОВЕРХНОСТИ ЭЛЛИПСОИДА ИЛИ ШАРА НА ПЛОСКОСТИ
Уравнения проекции в общем виде:
Х = f1(B, L); Y = f2(B, L)
B –широта, L – долгота
Х и Y – прямоугольные координаты
Конкретные реализации функций f1 и f2 часто выражены
сложными математическими зависимостями, а их число
практически не ограничено.
Z
Y
X
O
B
L

СЕТКИ КООРДИНАТ
В зависимости от положения оси системы сферических координат, используемой при проецировании, различаются:
Нормальная система – ось сферических координат совпадает с осью вращения Земли
Поперечная система – ось сферических координат лежит в плоскости экватора
Косая система – ось сферических координат расположена под углом к оси вращения Земли

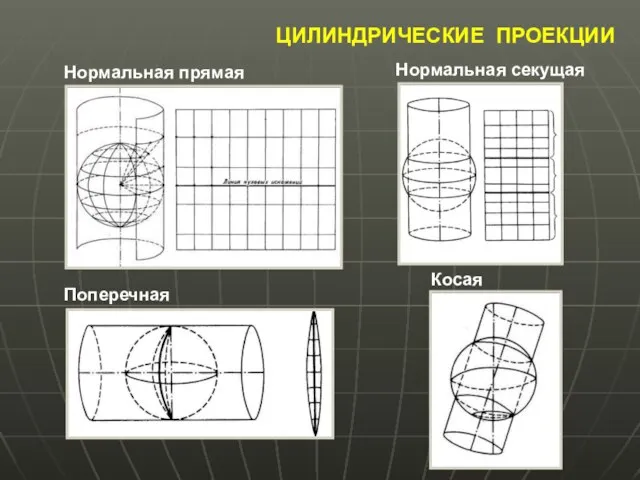
ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ

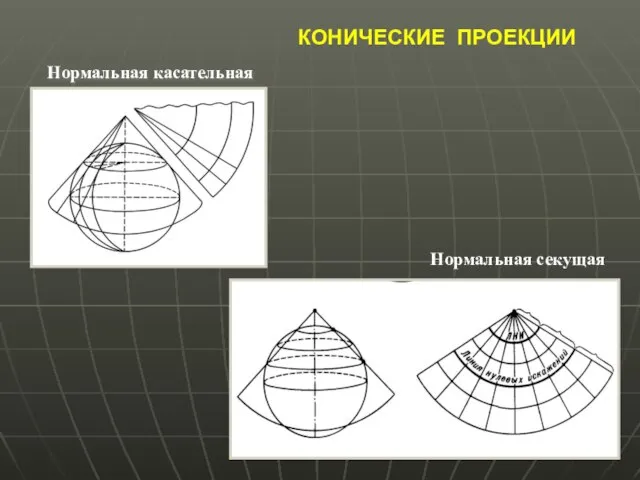
КОНИЧЕСКИЕ ПРОЕКЦИИ
Нормальная касательная
Нормальная секущая

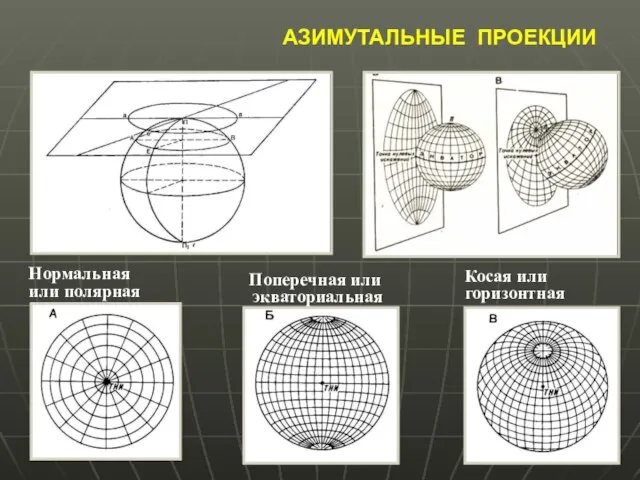
АЗИМУТАЛЬНЫЕ ПРОЕКЦИИ

АЗИМУТАЛЬНЫЕ ПРОЕКЦИИ ПОЛУШАРИЙ
Поперечная или
экваториальная
Нормальная или
полярная
Косая

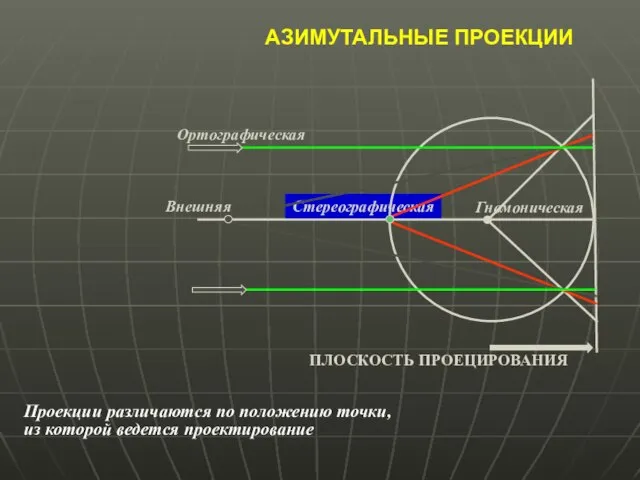
АЗИМУТАЛЬНЫЕ ПРОЕКЦИИ
Проекции различаются по положению точки,
из которой ведется проектирование

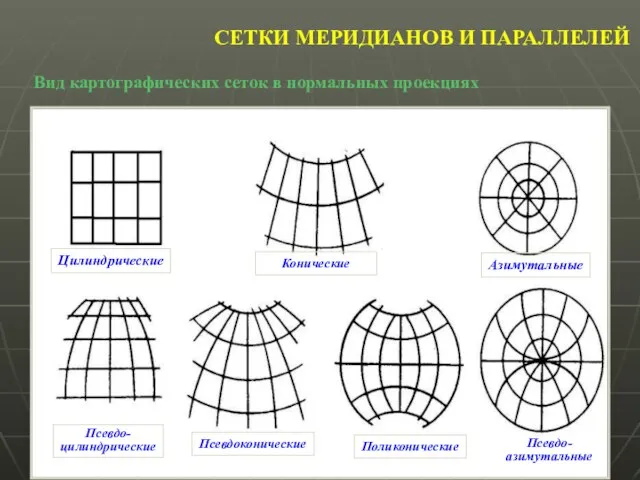
СЕТКИ МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ
Вид картографических сеток в нормальных проекциях

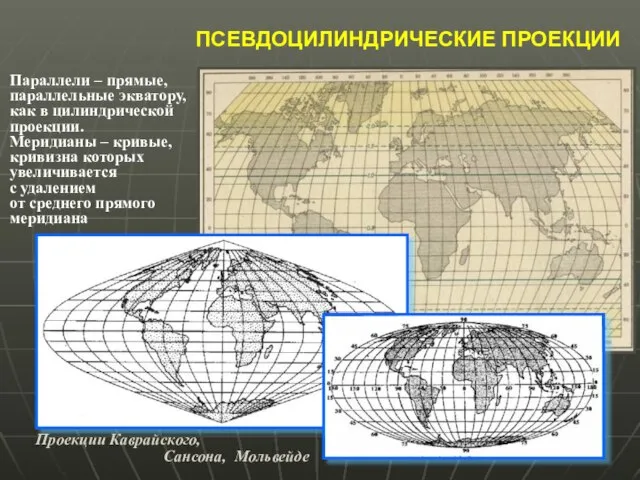
ПСЕВДОЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ
Параллели – прямые,
параллельные экватору,
как в цилиндрической
проекции.
Меридианы – кривые,
кривизна которых
увеличивается
с удалением
от среднего прямого
меридиана
Проекции Каврайского,
Сансона, Мольвейде

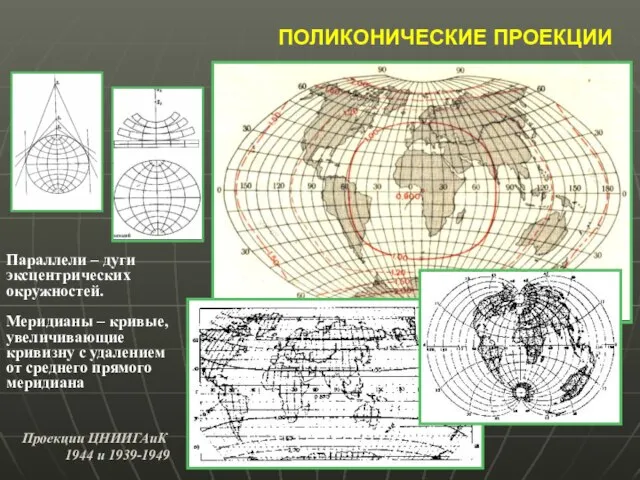
ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ
Параллели – дуги
эксцентрических
окружностей.
Меридианы – кривые,
увеличивающие
кривизну с удалением
от среднего прямого
меридиана
Проекции ЦНИИГАиК
1944 и 1939-1949

ПСЕВДОКОНИЧЕСКИЕ ПРОЕКЦИИ
Параллели – кривые,
меридианы – кривые, кривизна которых возрастает с удалением
от центрального прямого меридиана
Кардиоидальная проекция Вернера,
XVI век
Проекция Бонна

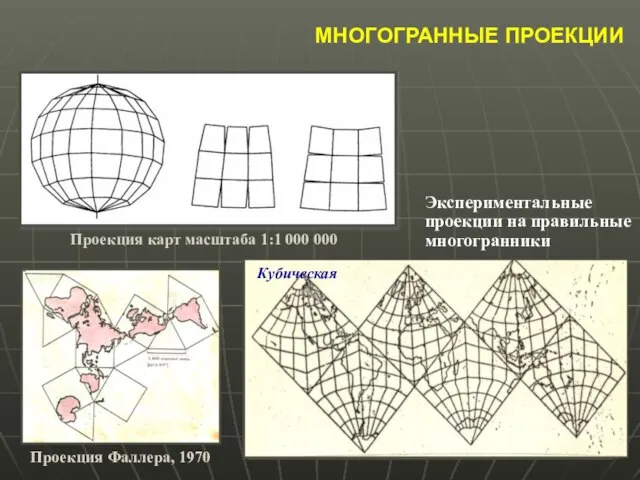
МНОГОГРАННЫЕ ПРОЕКЦИИ
Проекция карт масштаба 1:1 000 000
Проекция международной карты
масштаба 1:2 50 000
Проекция Фаллера, 1970
Экспериментальные
проекции на правильные
многогранники

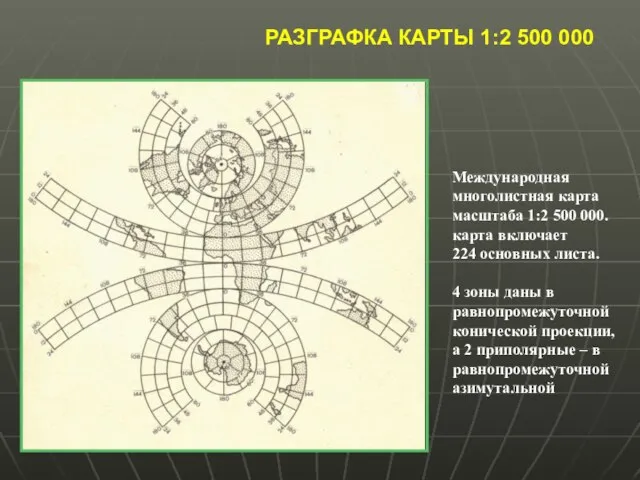
РАЗГРАФКА КАРТЫ 1:2 500 000
Международная многолистная карта
масштаба 1:2 500 000.
карта включает
224 основных листа.
4 зоны даны в
равнопромежуточной
конической проекции,
а 2 приполярные – в равнопромежуточной азимутальной

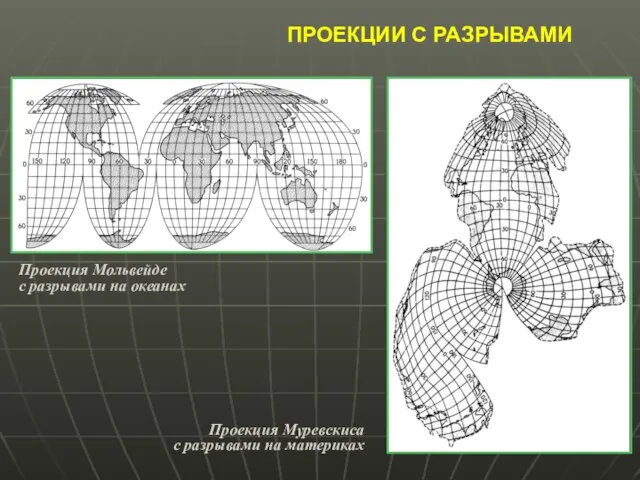
ПРОЕКЦИИ С РАЗРЫВАМИ
Проекция Мольвейде
с разрывами на океанах
Проекция Муревскиса
с разрывами на материках

КЛАССИФИКАЦИЯ ПРОЕКЦИЙ
Цилиндрические
Конические
Азимутальные
Псевдоцилиндрические
Псевдоконические
Псевдоазимутальные
Поликонические
Многогранные
Многополосные
Условные
Классификация по виду
нормальной картографической сетки

КЛАССИФИКАЦИЯ ПРОЕКЦИЙ
Равновеликие
Равноугольные
Произвольные, в том числе
Равнопромежуточные
- по меридианам
- по параллелям
Классификация
по характеру искажений

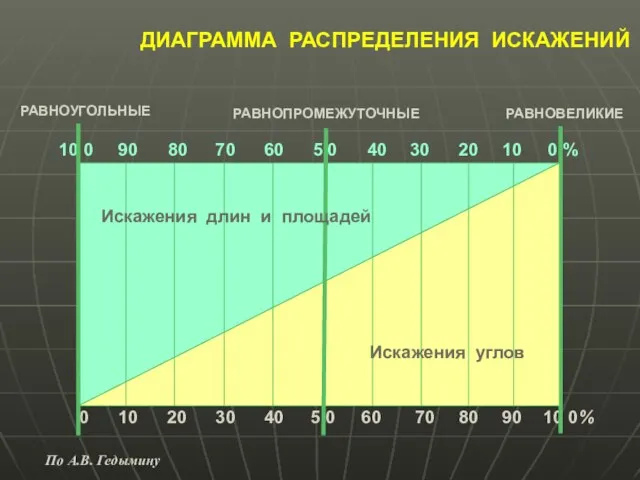
ДИАГРАММА РАСПРЕДЕЛЕНИЯ ИСКАЖЕНИЙ

ЭЛЛИПС ИСКАЖЕНИЙ
Эллипс искажений
или индикатриса Тиссо –
характеризует искажения
масштабов в данной точке (в центре эллипса)
а – направление наибольшего растяжения масштаба
b – направление наибольшего сжатия масштаба
m – масштаб по меридиану
n – масштаб по параллели
Виды искажений в проекциях:
Искажения длин (a и b)
Искажения площадей (р= m n Sinθ)
Искажения углов и форм (ω)
Искажения определяют:
аналитически
по номограммам
по картам с изоколами –
изолиниями искажений

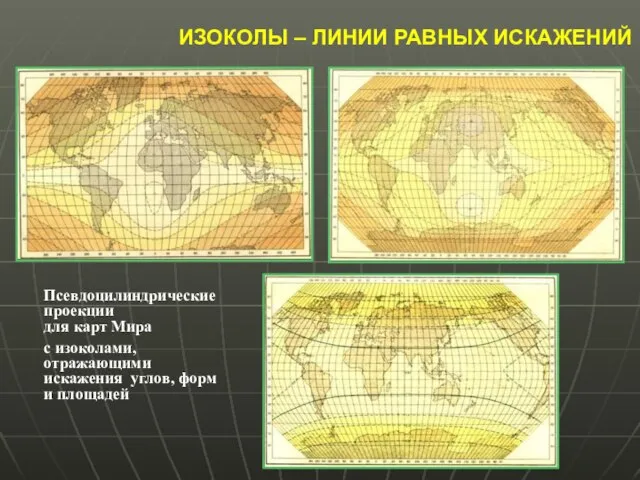
ИЗОКОЛЫ – ЛИНИИ РАВНЫХ ИСКАЖЕНИЙ
Псевдоцилиндрические проекции
для карт Мира
с изоколами, отражающими искажения углов, форм и площадей

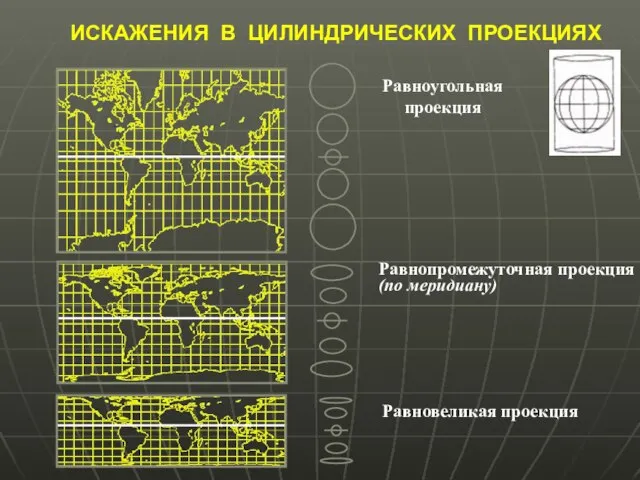
ИСКАЖЕНИЯ В ЦИЛИНДРИЧЕСКИХ ПРОЕКЦИЯХ
Равноугольная проекция
Равнопромежуточная проекция
(по меридиану)
Равновеликая проекция

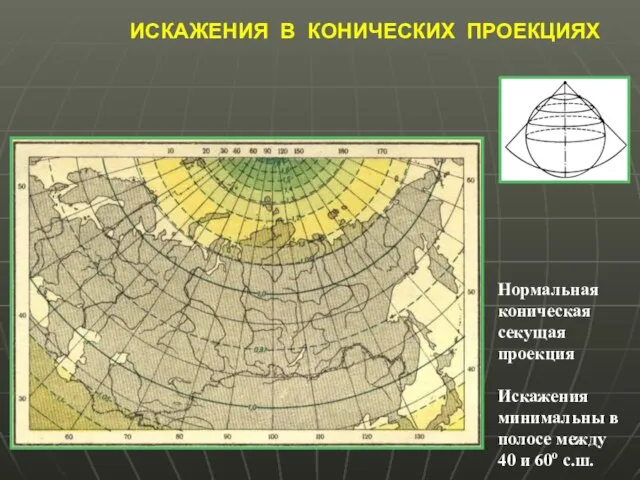
ИСКАЖЕНИЯ В КОНИЧЕСКИХ ПРОЕКЦИЯХ
Нормальная коническая
секущая
проекция
Искажения минимальны в полосе между
40 и 60о с.ш.

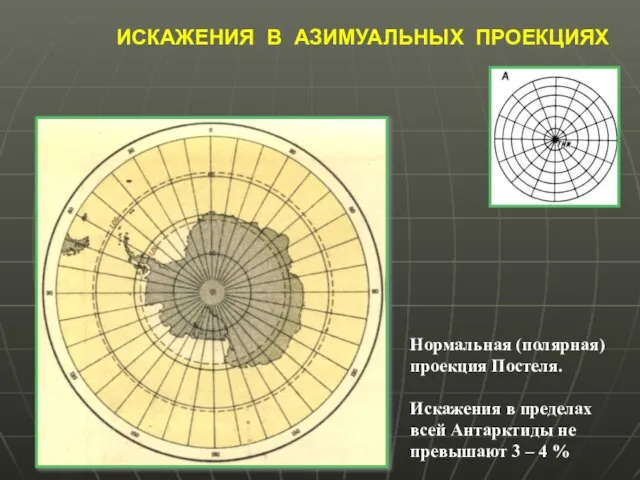
ИСКАЖЕНИЯ В АЗИМУАЛЬНЫХ ПРОЕКЦИЯХ
Нормальная (полярная)
проекция Постеля.
Искажения в пределах
всей Антарктиды не превышают 3 – 4 %

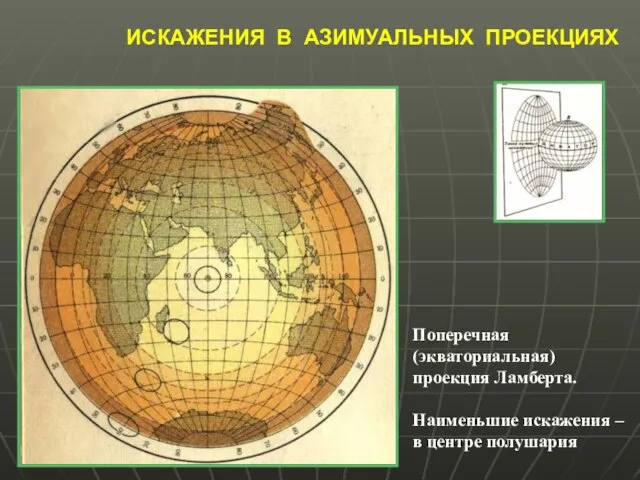
ИСКАЖЕНИЯ В АЗИМУАЛЬНЫХ ПРОЕКЦИЯХ
Поперечная
(экваториальная)
проекция Ламберта.
Наименьшие искажения –
в центре полушария

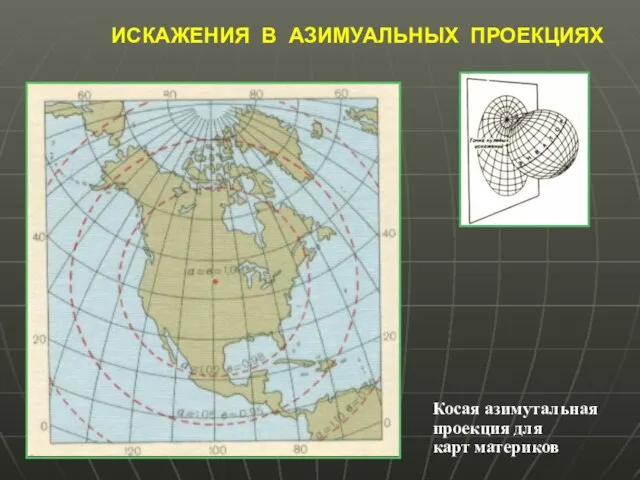
ИСКАЖЕНИЯ В АЗИМУАЛЬНЫХ ПРОЕКЦИЯХ
Косая азимутальная
проекция для
карт материков

ВЫБОР ПРОЕКЦИЙ
Условия выбора проекций:
Географические особенности территории, ее положение на Земном шаре, размеры и конфигурация
Назначение, масштаб, тематика карты, предполагаемый круг потребителей
Условия и способы использования карты, решаемые задачи, требования к точности измерений
Особенности самой проекции, величины искажения длин, площадей и углов, форма меридианов и параллелей, изображение полюсов и т. п.

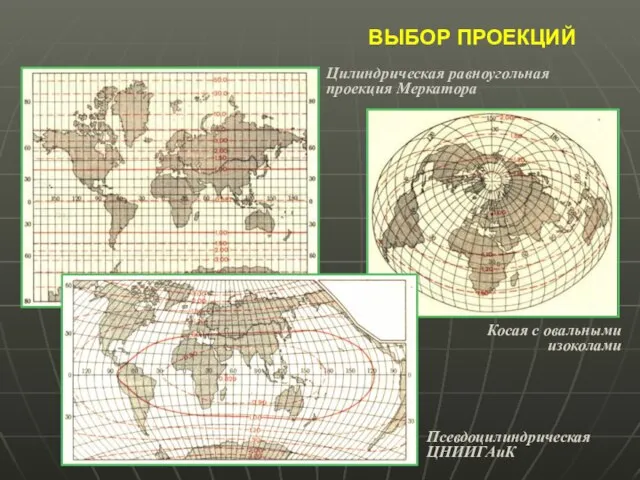
ВЫБОР ПРОЕКЦИЙ
Цилиндрическая равноугольная
проекция Меркатора
Псевдоцилиндрическая ЦНИИГАиК
Косая с овальными
изоколами

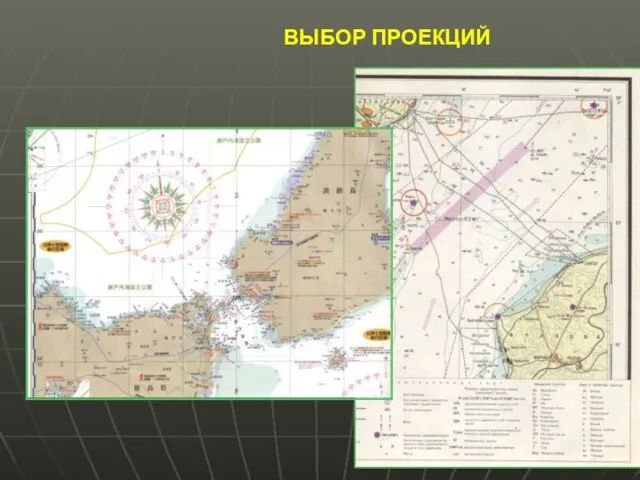
ВЫБОР ПРОЕКЦИЙ

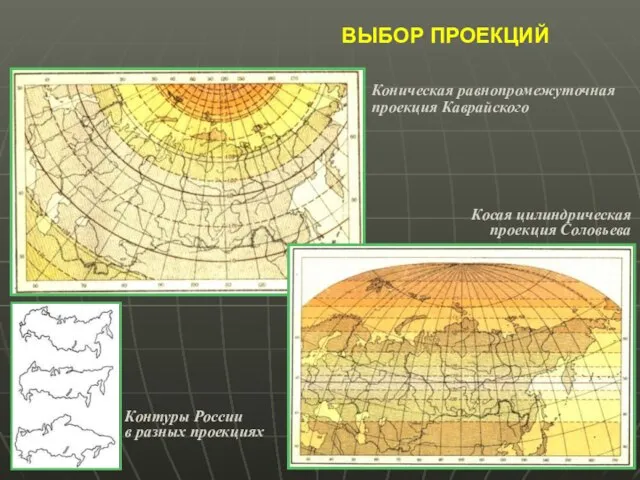
ВЫБОР ПРОЕКЦИЙ
Коническая равнопромежуточная
проекция Каврайского
Косая цилиндрическая
проекция Соловьева
Контуры России
в разных проекциях

В ЦЕНТРЕ МИРА
Атлас «Погляд на Украiну – Look at Ukraine», 1998

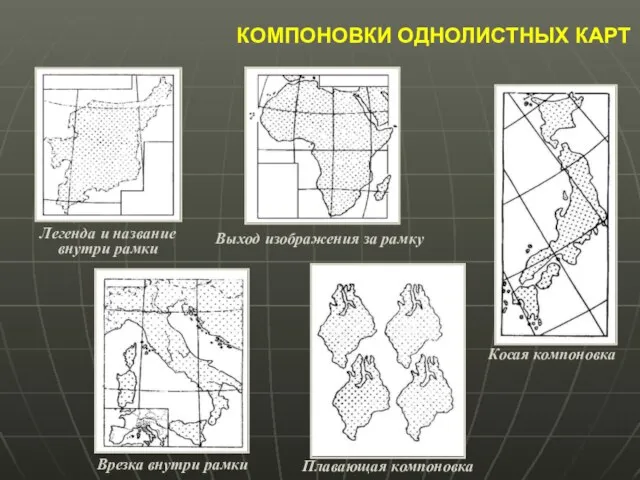
КОМПОНОВКИ ОДНОЛИСТНЫХ КАРТ

КОМПОНОВКИ ДЛЯ КАРТЫ МИРА
Нормальная цилиндрическая
проекция для карты мира
с разными центральными
меридианами:
а) целостное изображение
материков
б) целостное изображение
океанов

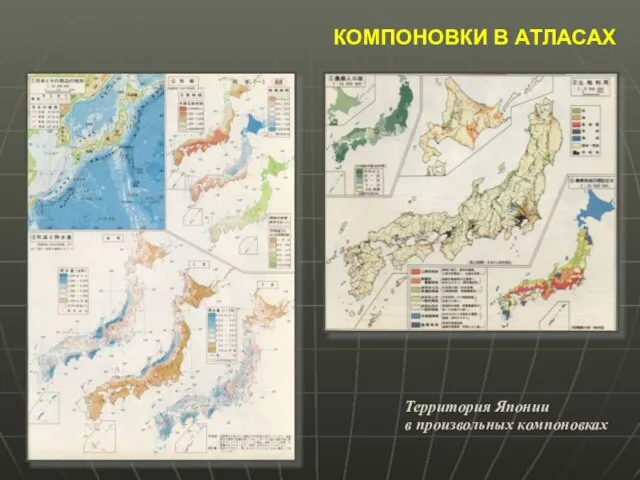
КОМПОНОВКИ В АТЛАСАХ
Территория Японии
в произвольных компоновках

КОМПОНОВКИ В АТЛАСАХ
Климатические карты оз. Байкал и острова Сахалин