Содержание
- 2. Оглавление: Оглавление 1. Введение. 2.Из истории развития функции 3. Способы задания функции 4. Класс элементарных функций.
- 3. Введение. Математика, давно став языком науки и техники, в настоящее время все шире проникает в повседневную
- 4. Из истории развития функции. Впервые функция вошла в математику под именем «переменная величина» в знаменитом труде
- 5. Из истории развития функции. С развитием науки понятие функции уточнялось и обобщалось. Сейчас оно стало настолько
- 6. Способы задания функций. Существуют три основных способа выражения зависимостей между величинами: табличный, графический и аналитический («формульный»).
- 7. Способы задания функций Графический способ представления зависимостей также является одним из средств их фиксации при изучении
- 8. Класс элементарных функции К элементарным функциям относятся практически все функции, встречающиеся в школьном учебнике. Прежде всего,
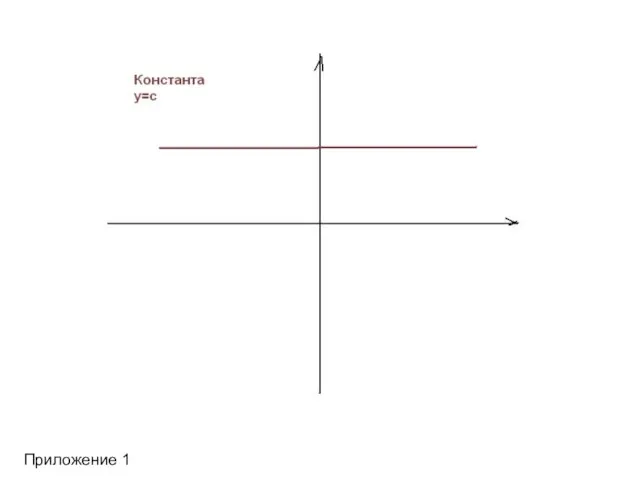
- 9. Приложение 1
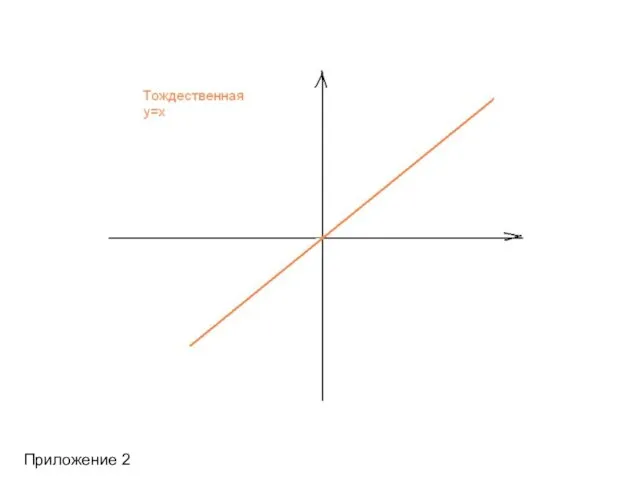
- 10. Приложение 2
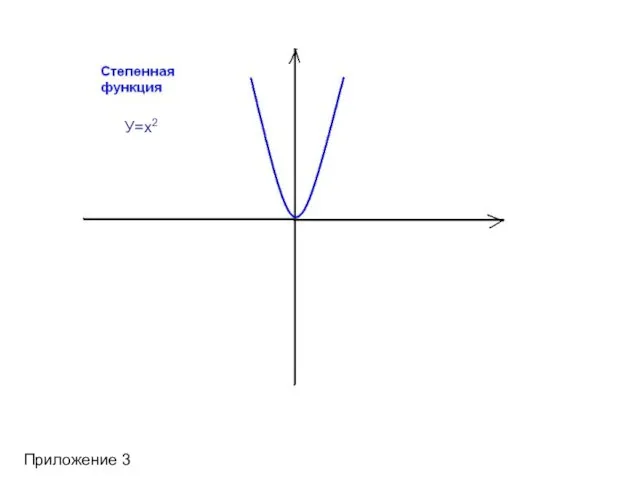
- 11. Приложение 3 У=х2
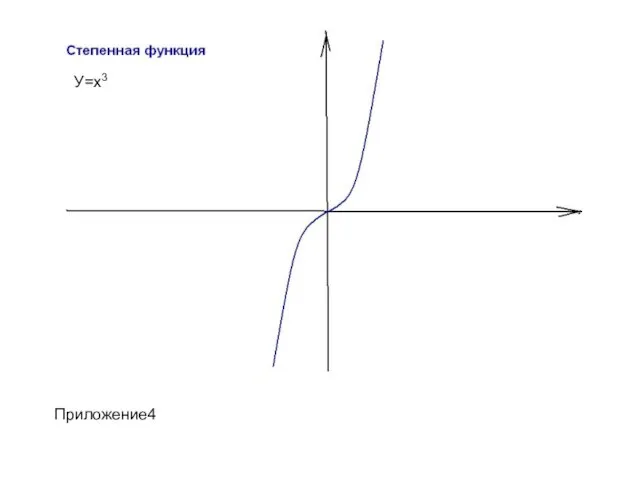
- 12. У=х3 У=х3 Приложение4
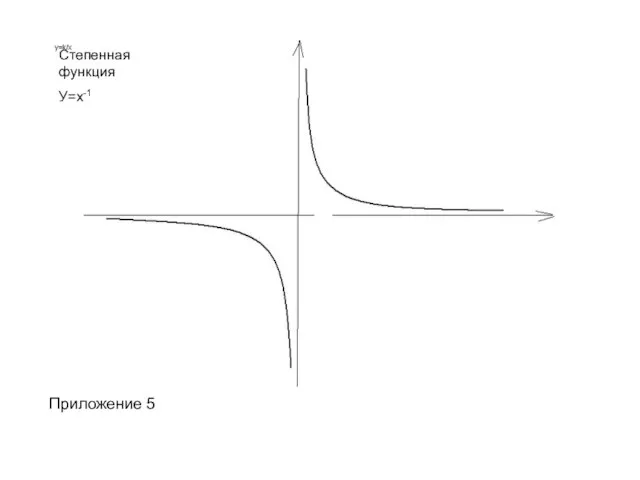
- 13. Степенная функция У=х-1 Степенная функция У=х-1 Приложение 5
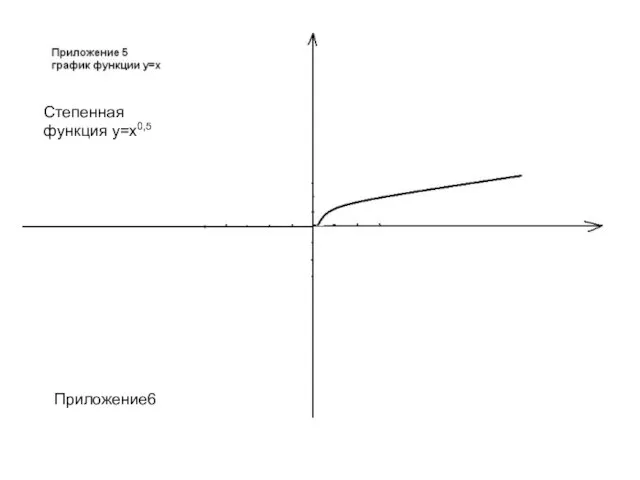
- 14. Приложение6 Приложение6 Степенная функция у=х0,5
- 15. Образование класса элементарных функций Имея определенный набор базисных функций f1 , f2 ,f3 ,...fk и допустимых
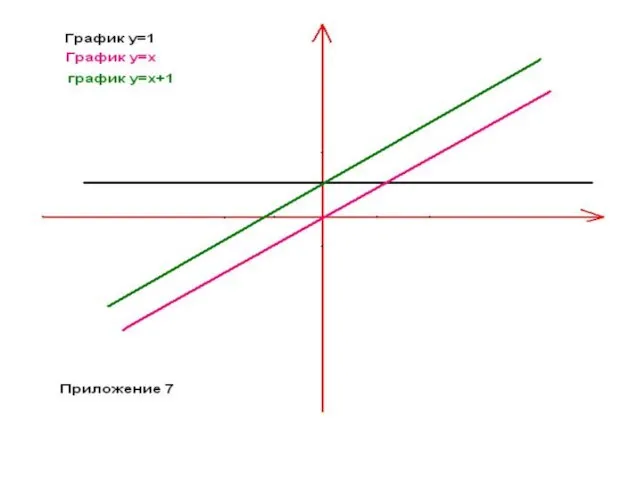
- 16. Построение графиков Чтобы построить график функции у= х +1, надо к графику функции у=х прибавить график
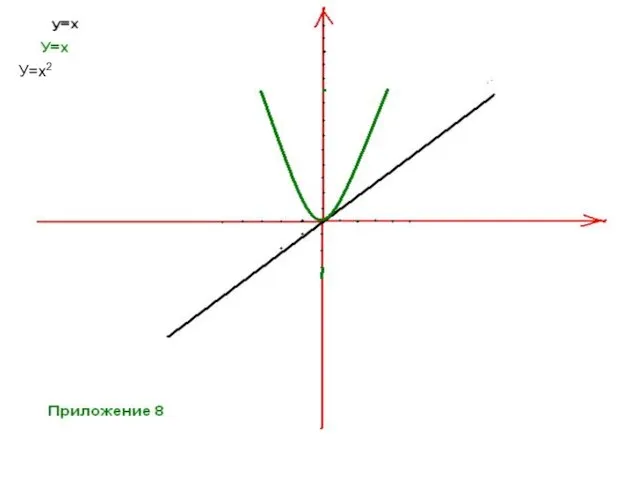
- 18. Построение графиков графика. Для построения графика функции у=х2 достаточно выполнить действие умножение с графиками двух тождественных
- 19. У=х2 У=х2
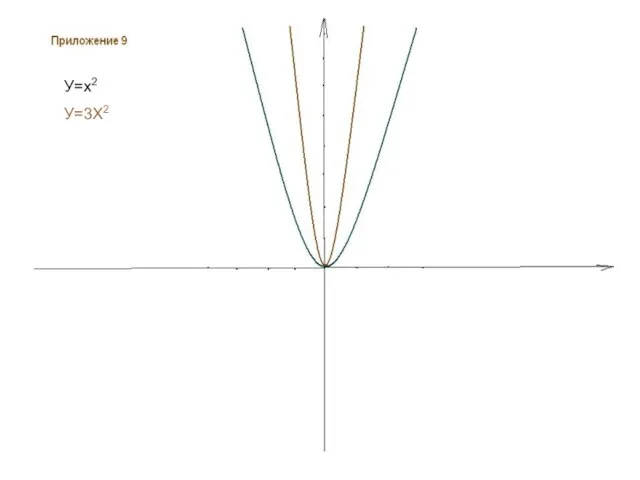
- 20. Построение графиков Для построения графика функции у= 3х2 надо график функции у= х2 умножить на 3.
- 21. У=х2 У=3Х2 У=х2 У=3Х2
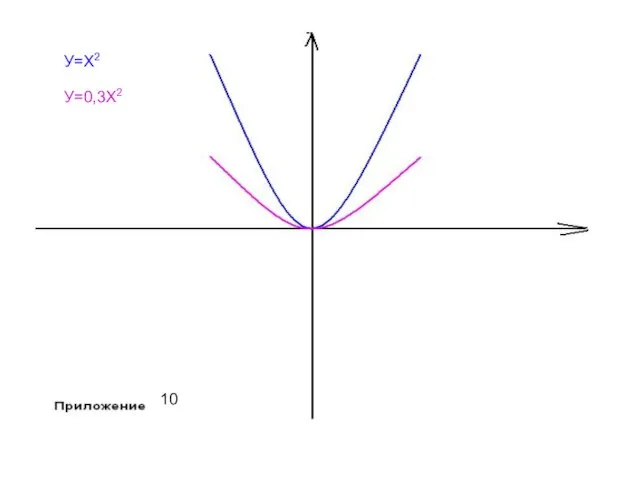
- 22. У=Х2 У=Х2 У=0,3Х2 10
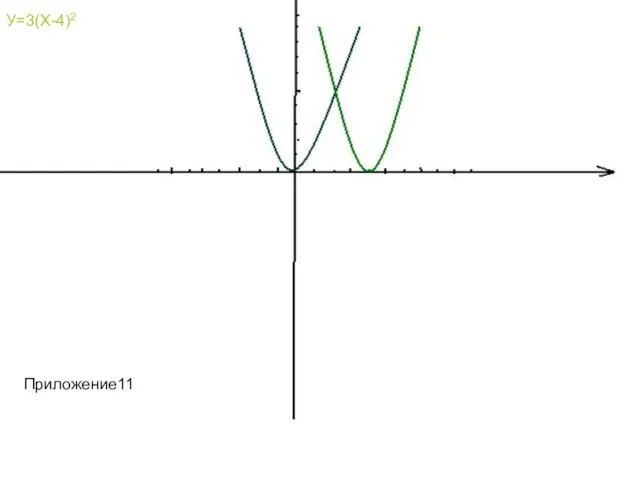
- 23. Построение графиков График функции у=3(х -4)2 можно получить, выполнив следующие действия: - сложить графики тождественной функции
- 24. У=3Х2 У=3Х2 У=3(Х-4)2 Приложение11
- 25. Преобразования исходного графика функции y= f(x). Из вышесказанного можно сделать следующий вывод, что выполняя различные действия
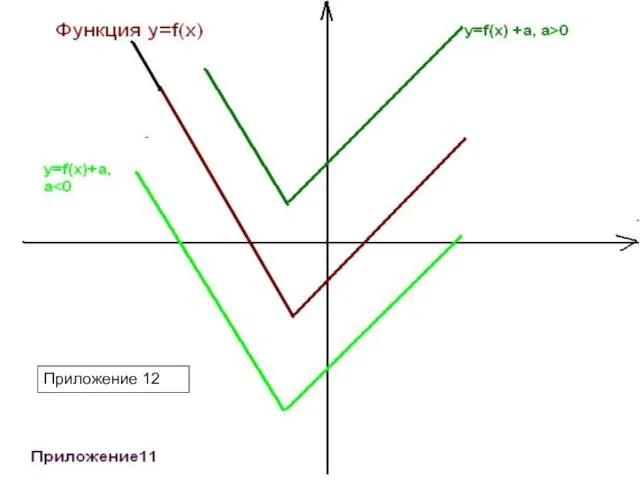
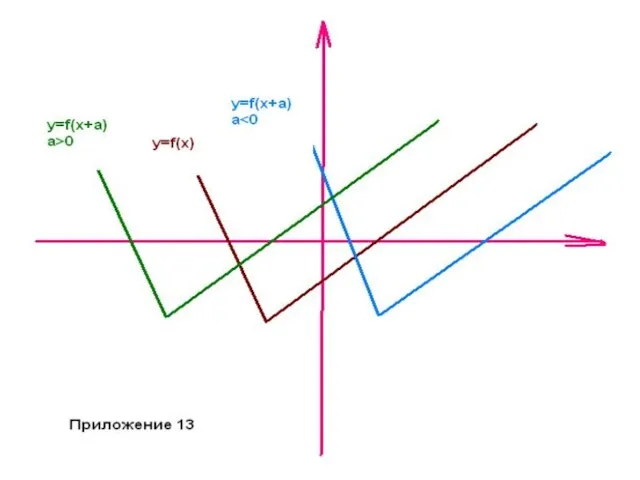
- 26. Преобразования исходного графика функции y= f(x). Параллельный перенос. а)y= f(x)+а – сдвиг по оси Оу на
- 27. Приложение 12 Приложение 12
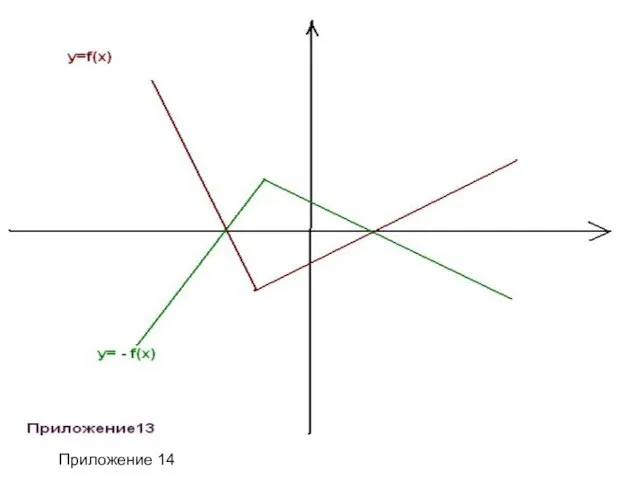
- 29. Преобразования исходного графика функции y= f(x). Симметрия относительно оси Ох. а) у=- f(x) – симметричное отражение
- 30. Приложение 14 Приложение 14
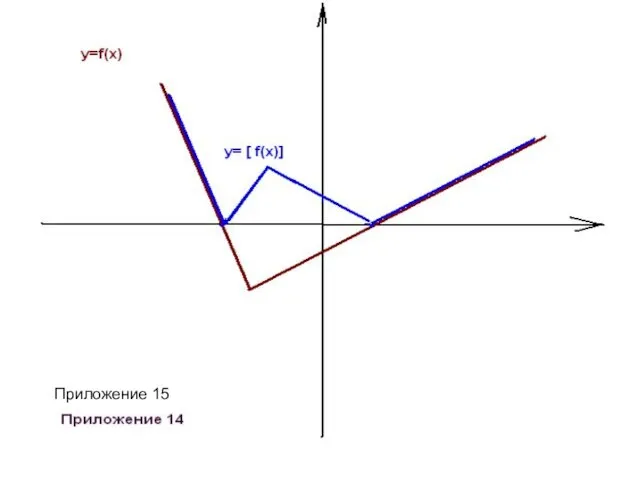
- 31. Приложение 15 Приложение 15
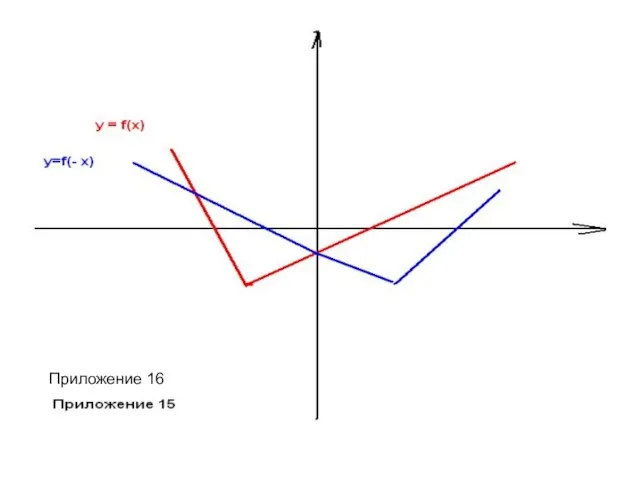
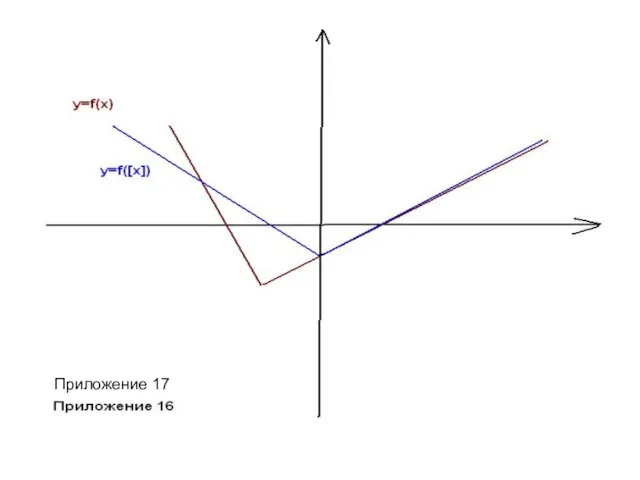
- 32. Преобразования исходного графика функции y= f(x). Симметрия относительно оси Оу. а) у = f(-x) – симметричное
- 33. Приложение 16 Приложение 16
- 34. Приложение 17 Приложение 17
- 35. Заключение. Заканчивая свою работу я увидел, что строить графики элементарных функций интересно и просто. А график
- 37. Скачать презентацию

















 Speaking about the weather
Speaking about the weather Что изучает физика?
Что изучает физика? Мифы о журналистике. То, что вы хотели знать, но боялись спросить
Мифы о журналистике. То, что вы хотели знать, но боялись спросить Строительно-монтажные работы при восстановлении объектов ж/д транспорта при возникновении ЧС
Строительно-монтажные работы при восстановлении объектов ж/д транспорта при возникновении ЧС Ремонт ленточного накопителя IBM 3590
Ремонт ленточного накопителя IBM 3590 Деление дробей
Деление дробей Развитие творческой деятельности школьников в рамках работы лаборатории ранней профессиональной ориентации
Развитие творческой деятельности школьников в рамках работы лаборатории ранней профессиональной ориентации Цветотип
Цветотип Формирование ключевых компетенций на уроках географии
Формирование ключевых компетенций на уроках географии Презентация на тему С огнем не играй - пожар не затевай!
Презентация на тему С огнем не играй - пожар не затевай! Наши любимые сказки Андерсена
Наши любимые сказки Андерсена Soonest пункт выдачи заказов
Soonest пункт выдачи заказов Глобальная сеть интернет
Глобальная сеть интернет Презентация на тему Древние германцы и Римская империя
Презентация на тему Древние германцы и Римская империя  AIESEC
AIESEC  Решение логических задач на олимпиадах по обществознанию (методические указания и комментарии к оцениванию)
Решение логических задач на олимпиадах по обществознанию (методические указания и комментарии к оцениванию) ALTA Personnel Pharma & Medical Equipment
ALTA Personnel Pharma & Medical Equipment Осложнения интубации трахеи
Осложнения интубации трахеи А. С. Грибоедов
А. С. Грибоедов Порядок начисления простых процентов. Лекция 2
Порядок начисления простых процентов. Лекция 2 Курсовая работа на тему: В стране выученных уроков
Курсовая работа на тему: В стране выученных уроков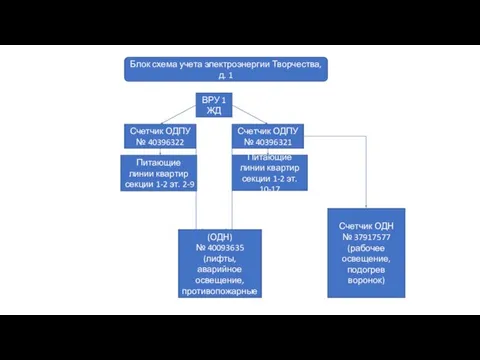 блок схема Творчества, д. 1
блок схема Творчества, д. 1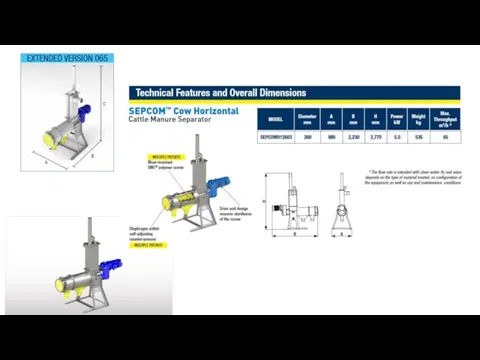 Solid Separator
Solid Separator Результативность системы воспитания детей и молодежи Великого Новгорода
Результативность системы воспитания детей и молодежи Великого Новгорода Тонкая палитра оттенков
Тонкая палитра оттенков инъекции
инъекции Внеклассные мероприятия на основе православных традиций
Внеклассные мероприятия на основе православных традиций Информатизация школьного образовательного пространства
Информатизация школьного образовательного пространства