Слайд 2NP-полнота задачи выполнимости
Задача выполнимости булевой функции:
Вход: булева функция, заданная формулой
Требуется определить, выполнима

ли функция, т.е. существует ли набор, на котором функция равно 1.
Теорема: Задача выполнимости булевой функции NP-полна.
Требуется доказать, что:
1. Эту задачу можно решить за полиномиальное время на НМТ.
2. Любую другую задачу класса NP можно свести к задаче выполнимости.
Слайд 3NP-полнота задачи выполнимости
1. Алгоритм на НМТ для задачи выполнимости:
1. Выбираем набор значений

переменных
2. Вычисляем значение функции на данном наборе
Слайд 4NP-полнота задачи выполнимости
2. Сведение произвольного языка L∈NP к задаче выполнимости:
Пусть M∈НМТ, L(M)=L
Пусть

входом M является слово w.
Покажем, как по M и w построить (за время, ограниченное полиномом) булеву функцию w0, выполнимую т. и т.т. когда M распознаёт w.
Т.к. M распознаёт w, то ∃ Q0, Q1, …, Qq – последовательность состояний M, такая, что Q0 – начальное, а Qq – допустимое.
Слайд 5NP-полнота задачи выполнимости
Определим наборы переменных:
1. Ci,j,t = 1 т.и.т.т., когда i-ая клетка

на ленте машины M содержит символ Xj в момент времени t.
2. Sk,t = 1 т.и.т.т., когда M в момент времени t находится в состоянии qk.
3. Hi,t = 1 т.и.т.т., когда головка в момент t находится над i-ой клеткой
Свяжем эти переменные ограничениями, которые будут истинны только для M на w
Q0, Q1, …, Qq –такая, что Q0 – начальное, а Qq – допустимое.
Слайд 6NP-полнота задачи выполнимости
Утверждение о Q0, Q1, …, Qq равносильно следующему:
В каждом состоянии

головка находится ровно над одной ячейкой
В каждом состоянии в каждой клетке ленты ровно один символ
Каждое состояние Qi, машина находится ровно в одном внутреннем состоянии
При одном переходе может изменится только та клетка, где головка
Изменение состояния происходит в соответствии с функцией переходов
Первое состояние является начальным
Последнее состояние - заключительное





 Легенда о Змеиной горе
Легенда о Змеиной горе Обучение защитным действиям в баскетболе
Обучение защитным действиям в баскетболе Страдательные причастия настоящего времени
Страдательные причастия настоящего времени Повышение качества преподавания математики, информатики
Повышение качества преподавания математики, информатики Вакансии банка Открытие
Вакансии банка Открытие ПРОДВИЖЕНИЕ В ПОИСКОВЫХ СИСТЕМАХ Роскошь или эффективное средство развития бизнеса? Реалии современного Рунета
ПРОДВИЖЕНИЕ В ПОИСКОВЫХ СИСТЕМАХ Роскошь или эффективное средство развития бизнеса? Реалии современного Рунета Высокотехнологичные методы лечения ревматоидного артритаКардиологический диспансерИлюшина Лариса Викторовнаг. Сыктывкар
Высокотехнологичные методы лечения ревматоидного артритаКардиологический диспансерИлюшина Лариса Викторовнаг. Сыктывкар Ятрогенные преступления
Ятрогенные преступления МЁД «Лесные Угодья»
МЁД «Лесные Угодья» Бог и человек
Бог и человек Вторжение на советскую землю началось На улицах осажденного Ленинграда.
Вторжение на советскую землю началось На улицах осажденного Ленинграда. Презентация на тему Переживания, испытанные временем (4 класс)
Презентация на тему Переживания, испытанные временем (4 класс) Кейс из Курска. Из местной компании в международную франшизу за 3 года
Кейс из Курска. Из местной компании в международную франшизу за 3 года Методы хроматографии. Ионообменная хроматография
Методы хроматографии. Ионообменная хроматография Методикаразработки административных регламентов предоставления государственных услуг и административных регламентов исполнен
Методикаразработки административных регламентов предоставления государственных услуг и административных регламентов исполнен Народное творчество
Народное творчество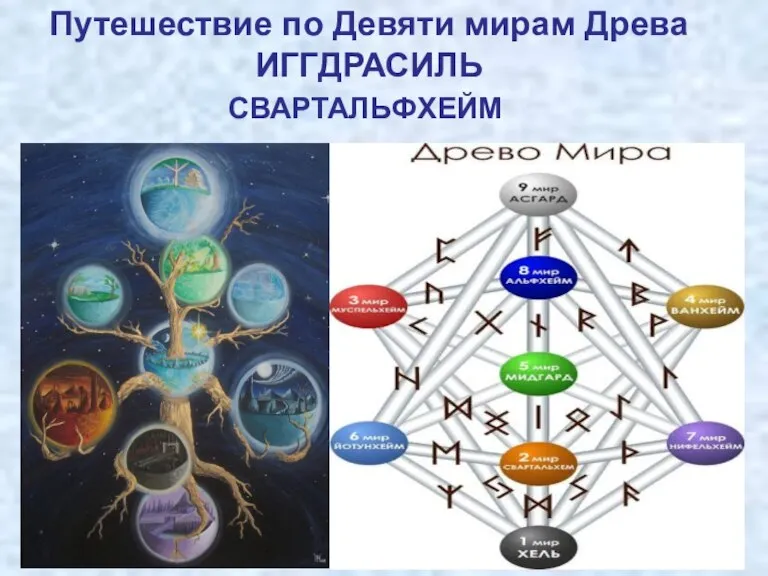 Рунические миры Свартальфхейм
Рунические миры Свартальфхейм ЭКСПЕРТНАЯ СИСТЕМА FILTEX32 ДЛЯ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ ПОЛОСНО-ПРОПУСКАЮЩИХ МИКРОПОЛОСКОВЫХ ФИЛЬТРОВ Беляев Б.А., Б
ЭКСПЕРТНАЯ СИСТЕМА FILTEX32 ДЛЯ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ ПОЛОСНО-ПРОПУСКАЮЩИХ МИКРОПОЛОСКОВЫХ ФИЛЬТРОВ Беляев Б.А., Б Когда появилась одежда?
Когда появилась одежда? 20171028_trudovye_resursy._rynok_truda
20171028_trudovye_resursy._rynok_truda Планета Юпитер
Планета Юпитер Презентация на тему Перпендикуляр и наклонная
Презентация на тему Перпендикуляр и наклонная  Таня Савичева
Таня Савичева Токарный станок и режущий инструмент
Токарный станок и режущий инструмент  Атмосферные фронты. Циклоны и антициклоны 8 класс
Атмосферные фронты. Циклоны и антициклоны 8 класс За нами – Москва! 7 класс
За нами – Москва! 7 класс Оформление изделий в технике Декупаж
Оформление изделий в технике Декупаж Контактная сеть
Контактная сеть