Клітинкові автомати

Лекція 15. Комп’ютерні моделі.
Моделювання динамічних систем
Клітинкові автомати.
Якщо стан дискретної системи у певний момент часу залежить лише від попереднього її стану та правил переходу, то вона називається автоматом.
Клітинковий автомат – клас повністю дискретних геометричних моделей, поведінка яких визначається просторово локальними залежностями. У такий спосіб вдається зв’язати процеси на мікрорівні з макрорівневими змінами досліджуваного об’єкта.
Гра “Життя” (Конвей, 1970).
“Всесвіт” поділено на клітинки, у кожній з яких є або немає життя. У кожний дискретний момент часу стан клітинки визначається станом восьми її сусідів за правилами:
Пуста клітина, що має 3 “живих” сусіди – “оживає”;
Якщо сусідів менше двох (“одинокість”), або більше трьох (“перенасе-лення”) “життя” у ній зникає.

Лекція 15. Комп’ютерні моделі.
Моделювання динамічних систем
Формально клітинковий автомат визначимо як модель Α (λ, ε, ν, φ), що складається з:
λ – регулярна просторова сітка однакових клітинок (сот). У двовимірному випадку найчастіше це сітка квадратів, або правильних шестигранників;
ε – обмежена множина станів, у яких можуть знаходитись клітинки автомата по ходу його еволюції;
ν (с) – множина сусідів, які мають вплив на центральну клітину (с);
φ – правила, які визначають спосіб переходу клітинки від поточного стану до наступного, відповідно до стану її сусідів з множини ν. Ці правила можуть мати детермінований, або ймовірносний характер
φ: et (ν (с) )→ et+1 (с), де e є ε.
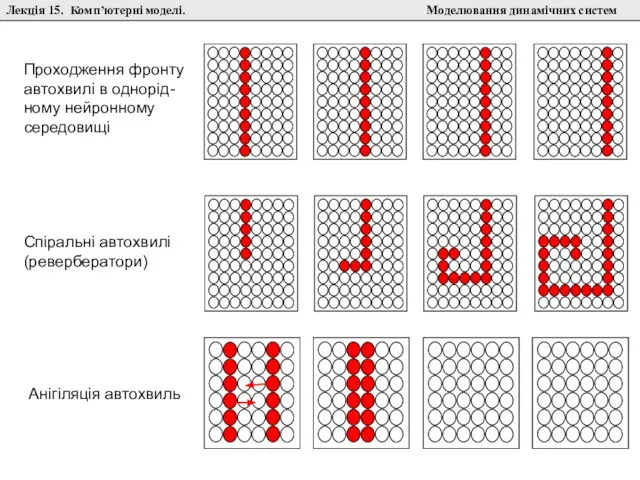
Клітинковий автомат є імітаційною математичною моделлю, де дискретними є не тільки незалежні змінні, а й шукані розв’язки.

Лекція 15. Комп’ютерні моделі.
Моделювання динамічних систем
Модель Вінера-Розенблюта.
Змоделюємо мережу нейронів двовимірною чотирикутною регулярною сіткою λij (I =1..n, j =1..m)
Правила переходу:
Правила зміни рівня активації:
де q – деякий параметр часової релаксації збудження, а коефіцієнт Ckl визначає величину сигнала активації від сусіда, наприклад у найпростішому випадку:
Окіл Мура

Лекція 15. Комп’ютерні моделі.
Моделювання динамічних систем
Анігіляція автохвиль
Спіральні автохвилі (ревербератори)
Проходження фронту автохвилі в однорід-ному нейронному середовищі

Лекція 15. Комп’ютерні моделі.
Моделювання динамічних систем
Застосування в медицині.