Колебание нити, подвешенной за один конец

Свободные колебания подвешенной нити
Будем рассматривать малые колебания такие, что можно пренебречь квадратом производной по сравнению с единицей. Дифференциальное уравнение малых колебаний подвешенной нити:
Здесь

Краевые условия
Задача о колебании подвешенной нити сводится к интегрированию уравнения с граничным условием:
А также с начальными условиями:

Задача сводится к решению уравнения:
Решение будем искать в виде:
Получаем два уравнения:

Решения
При решении используются функции Бесселя
напомним уравнение Бесселя
Где решением будет функция:
Тогда решения требуемых 2-х уравнений будут:

Получим решение
Где коэффициенты, найденные с помощью начальных условий, равны соответственно:

Практическая задача
Тяжелая однородная нить длины , закрепленная верхним концом, в начальный момент отклонена от вертикальной оси на угол a (рад.). найти отклонение нити в любой момент времени.
Начальные условия: Рисунок:

Решение
Функция Бесселя 1-го рода будет равна:
Решение этой задачи запишем в виде:
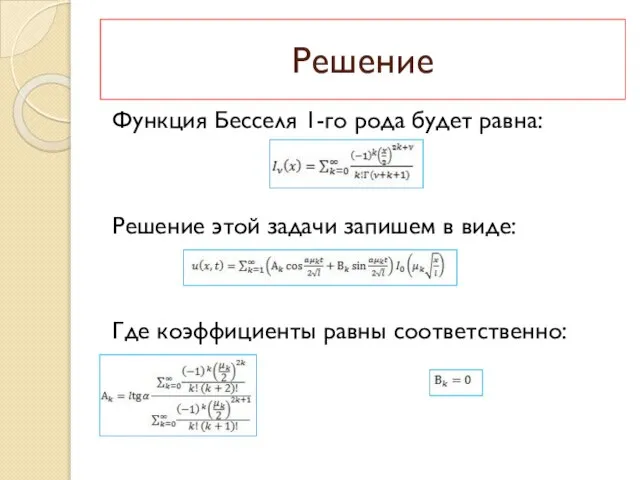
Где коэффициенты равны соответственно:

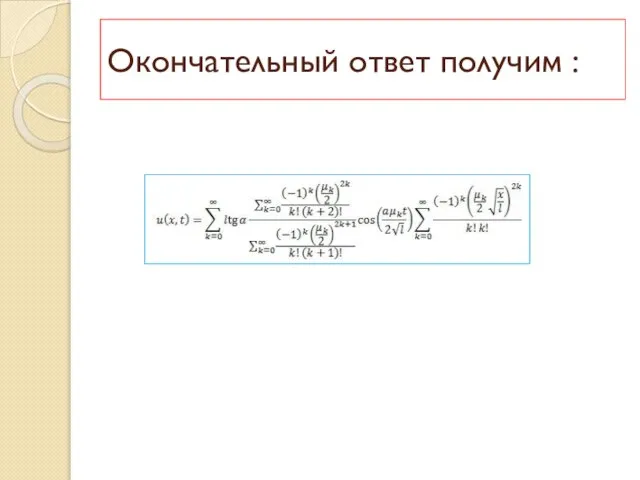
Окончательный ответ получим :