Комплексные числа

N C Z C Q C R C C
N- ”natural” R- “real” C - “complex” Z – исключительная роль нуля “zero”
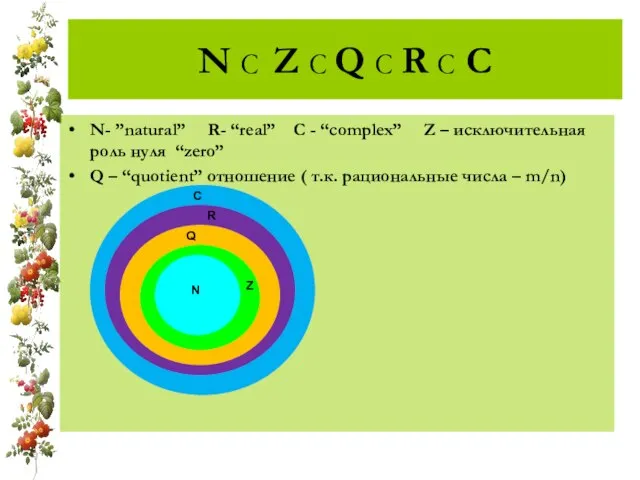
Q – “quotient” отношение ( т.к. рациональные числа – m/n)
C
R
Q
Z
N

Минимальные условия комплексного числа
1) Существует число, квадрат которого = -1.
2) Множество комплексных чисел содержит все действительные числа.
3) Операции сложения, вычитания, умножения и деления комплексных чисел удовлетворяет обычным законом арифметических действий.

Элемент, квадрат которого равен -1 называется мнимой единицей. Обозначается i (переводится «мнимый», «воображаемый»)
"Комплексными числами и функциями комплексного переменного математики пользовались в своих исследованиях уже в XVIII в. Особенно велики заслуги крупнейшего математика XVIII в. Леонарда Эйлера (1707—1783), который по праву считается одним из творцов теории функций комплексного переменного. В замечательных работах Эйлера детально изучены элементарные функции комплексного переменного.
После Эйлера открытые им результаты и методы развивались, совершенствовались и систематизировались, и в первой половине XIX в. теория функций комплексного переменного оформилась как важнейшая отрасль математического анализа. "Первое упоминание о «мнимых» числах как о корнях квадратных и» отрицательных чисел относится еще к XVI в. (Дж. К а р д а н о, 1545). До середины XVIII в. комплексные числа появляются лишь эпизодически в трудах отдельных математиков (И. Ньютон, Н. Бернулли, А. Клеро). Первое изложение теории комплексных чисел на русском языке принадлежит Л. Эйлеру («Алгебра», Петербург, 1763, позднее книга была переведена на иностранные языки и многократно переиздавалась): символ «i» также введен Л. Эйлером. Геометрическая интерпретация комплексных чисел относится к концу XVIII в. (датчанин Каспар Вессель, 1799 г.)."

Условия про операции комплексных чисел позволяют умножать комплексные числа на мнимую единицу ( i ). Такое произведение называют чисто мнимыми числами.
Например: i, 2i, -0,3i – чисто мнимые числа.
3i +13i=(3+13)i = 16i
3i·13i = (3·13) (i·i)=39i2=-39
ПРАВИЛА АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
10 ai+bi=(a+b)i 20 a(bi)=(ab)i
30 (ai)(bi)=abi2= -ab 40 0i =0

Сумма a+bi (a и b действительные числа)
а = 0, то a+bi =0+bi=bi (мнимое)
b = 0, то a+bi =а+0=а ( действительное)
а не равно нулю, то a+bi ни действительное, не мнимое. Оно более сложное составное число.
КОМПЛЕКСНЫМИ ЧИСЛАМИ НАЗЫВАЮТ СУММУ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА И ЧИСТО МНИМОГО ЧИСЛА
Z=a + bi

Кк
КОМПЛЕКСНЫЕ ЧИСЛА РАВНЫ, КОГДА РАВНЫ ИХ ДЕЙСТВИТЕЛЬНЫЕ И МНИМЫЕ ЧАСТИ.
a+bi=c+di, если a=c, b=d
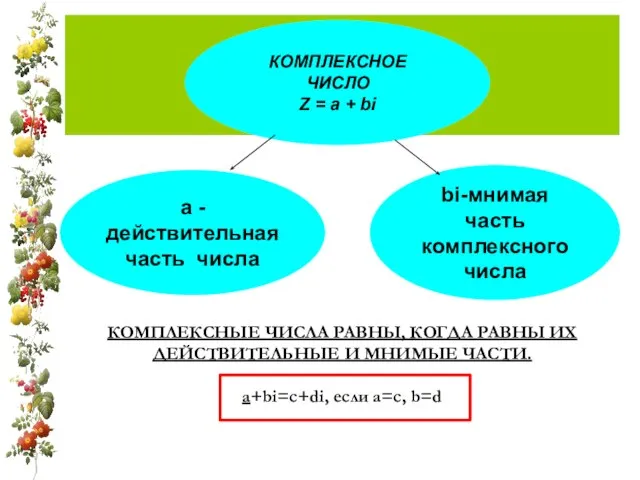
КОМПЛЕКСНОЕ ЧИСЛО
Z = a + bi
а - действительная часть числа
bi-мнимая часть комплексного числа