Конические сечения

Содержание
История исследования
(19 столетий ожидания)
Коника
Экспериментальное доказательство
Вездесущий эллипс/применение конических сечений
Словарь
Список источников

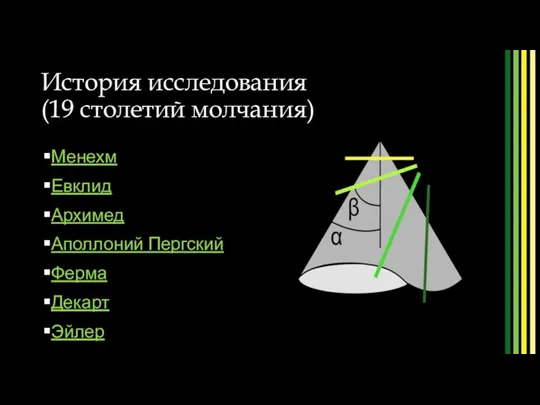
История исследования
(19 столетий молчания)
Менехм
Евклид
Архимед
Аполлоний Пергский
Ферма
Декарт
Эйлер

Менехм (IV в. до н. э.)
Впервые конические сечения (10) появились у Менехма (IV в. до н. э.).
Он рассматривал остроугольный, прямоугольный и тупоугольный конусы (11) и каждый из них пересекал плоскостью, перпендикулярной одной из образующих (13).
В первом случае в сечении с поверхностью конуса получался эллипс (35) (рис. 1), во втором — парабола (17) (рис. 2), в третьем — гипербола (6), точнее, одна, ветвь гиперболы (рис. 3).­
Фактически он пользовался прямоугольными координатами на плоскости: за начало координат принимал вершину кривой второго порядка (12), за одну из координатных осей – главный диаметр, а другую ось проводил перпендикулярно первой в плоскости, в которой лежит кривая.

Евклид (III в. до н. э.)
С именем Евклида связывают становление александрийской математики (геометрической алгебры) как науки.
В XI книге «Начал» дается следующее определение: если вращающийся около одного из своих катетов прямоугольный треугольник, слева вернется в то же самое положение, из которого он начал двигаться, то описанная фигура будет конусом (11). Неподвижный катет, вокруг которого поворачивается треугольник, называется осью конуса (11), а круг, описываемый вращающимся катетом, называется основанием конуса.
Евклид рассматривает только прямые конусы, т. е. такие, у которых ось перпендикулярна к основанию.

Архимед (ок. 287–212))
Разработал предвосхитившие интегральное исчисление методы нахождения площадей, поверхностей и объемов различных фигур и тел.
В трактате «О коноидах и сфероидах» Архимед рассматривает шар (32) (рис. 4), эллипсоид (36) (рис. 5), параболоид (18) (рис. 6) и гиперболоид (7) (рис. 7), вращения и их сегменты и определяет их объемы.
рис. 4
рис. 7
рис. 6
рис. 5
изображения автор: Sam Derbyshir

Архимед (ок. 287–212))

Аполлоний Пергский (ок. 260–ок. 170)
Аполлоний прославился в первую очередь выдающейся работой «Конические сечения» (8 книг), в которой дал содержательную общую теорию эллипса (35), параболы (17) и гиперболы (6).
Именно Аполлоний предложил общепринятые названия этих кривых; до него их называли просто «сечениями конуса».
Он ввёл и другие математические термины, латинские аналоги которых навсегда вошли в науку, в частности: асимптота (2), абсцисса, ордината.

Аполлоний Пергский (ок. 260–ок. 170)
рис. 9
В работе Аполлония «Конические сечения» восемь книг; до наших дней сохранилось семь.
В сравнении с Менехмом он становится на более общую точку зрения: берет произвольный конус, причем рассматривает две его полости, и пересекает конус плоскостью под разными углами. В случае, если плоскость пересекает все образующие(13) конуса, в ее пересечении с поверхностью конуса образуется эллипс; если она параллельна одной из образующих конуса – парабола; если плоскость пересекает обе полости конуса – гипербола.
Фактически Аполлоний пользуется косоугольной системой координат, принимая за начало координат любую точку Р кривой и направляя координатные оси по диаметру и по касательной к кривой, проходящих через точку Р.

Аполлоний Пергский (ок. 260–ок. 170)
рис. 9

Аполлоний Пергский (ок. 260–ок. 170)
рис. 9
Из других заслуг Аполлония перед наукой стоит отметить, что он переработал астрономическую модель Евдокса (рис. 10), введя эпициклы (37) и эксцентрики (33) для объяснения неравномерности движения планет. Эту теорию позднее развили Гиппарх и Птолемей.
Сочинения Аполлония не влияли на развитие науки до VIII века.
С появлением аналитической геометрии, механики и новой теории движения планет Кеплера наступило возрождение идей Аполлония. Таким образом, от создания теории Аполлония до ее применения на практике потребовалось 19 столетий.

Аполлоний Пергский (ок. 260–ок. 170)
рис. 9
Большой интерес представляют не только результаты Аполлония, но и методы, которыми он пользуется. В них можно найти многочисленные мотивы более поздних достижений математики — алгебры, аналитической, проективной геометрии и местами даже дифференциальной геометрии.
Книга оказала огромное влияние на творчество последующих математиков, включая Ферма, Декарта, Ньютона, Лагранжа и многих других.
Каким образом Аполлоний, не владея математическим анализом, сумел сделать свои открытия, неясно. Возможно, у него, как у Архимеда, был некий метод бесконечно малых, который он использовал в эвристических целях, чтобы затем передоказать результат каноническими средствами античной геометрии.
Ван дер Варден пишет:
«Аполлоний виртуозно владеет геометрической алгеброй, но не менее виртуозно умеет скрывать свой первоначальный ход мыслей. Из-за этого-то его книгу и трудно понимать; рассуждения его элегантны и кристально ясны, но что его привело именно к таким рассуждениям, а не к иным каким-нибудь, — об этом можно лишь догадываться».

Пьер Ферма (1601–1665)
рис. 9

Рене Декарт (1596–1650)
рис. 9
«Геометрия» (аналитическая геометрия) получила наибольшую известность.
«Геометрия» состоит из трех книг. Вопросы аналитической геометрии в ней разбросаны без особой системы по всем трем книгам.
В основу «Геометрии» положены две идеи: решение геометрических задач с помощью алгебры и метода координат и понятие переменной величины. «Поворотным пунктом в математике была декартова переменная величина. Благодаря этому в математику вошли движение и тем самым диалектика (8)» — написал Ф. Энгельс в работе «Диалектика природы».
Декарт подобно Ферма, чертил только одну координатную ось с начальной точкой, указывая направления других координат точек. Но иногда он проводил и две координатные оси, правда, располагая их необычным для нас образом. Кроме того, он, и Ферма, почти не употреблял отрицательных координат, что вынуждало его обрывать кривую точками, лежащими на координатных осях.

Леонард Эйлер (1707–1783)
рис. 9
В 1748 г. Эйлер опубликовал большое сочинение «Введение в анализ бесконечных» в двух томах, из которых первый том посвящен введению в анализ, а второй — аналитической геометрии.
Рассматриваются прямоугольные и косоугольные координаты точки на плоскости
Эйлер подробно излагает общую теорию кривых второго порядка, деля эти кривые на типы и приводя их уравнения к каноническим.
Он изучает также кривые третьего порядка, деля их на 16 родов, и кривые четвертого порядка (146 родов).
В основном Эйлер завершил работу систематизации аналитической геометрии.

Коника
Эллипс (+ частный случай окружность)
Парабола
Гипербола
Свойства конических сечений

Эллипс
рис. 9

Эллипс
рис. 9

Парабола
рис. 9

Парабола
рис. 9

Гипербола
рис. 9

Гипербола
рис. 9

Свойства конических сечений
рис. 9
Геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету называется:
эллипсом, если 0≤ε<1;
гиперболой, если ε>1;
параболой, если ε=1.
Эллипс, гипербола, парабола получаются в сечениях кругового конуса плоскостями и поэтому называются коническими сечениями. Это свойство также может служить геометрическим определением эллипса, гиперболы, параболы.

Экспериментальное доказательство
Опыт №1
(с вафельным стаканчиком)
Опыт №2
(с карманным фонариком)
Как начертить эллипс?

Опыт № 1
рис. 9

Опыт № 2
рис. 9

Как начертить эллипс?
рис. 9

Вездесущий эллипс
рис. 9

Словарь

Словарь

Словарь

Словарь

Список источников
Галкин Е. В. Краткая история математики. – М.: АСТ, 2003. – 229с.
Карпушина Н. Во власти сечений//Наука и жизнь, 2012. № 5.
Асимптота//Википедия: [https://ru.wikipedia.org]. – Режим доступа: https://ru.wikipedia.org (Дата обращения: 14.04.2019)
Гипербола (математика)//Википедия: [https://ru.wikipedia.org]. – Режим доступа: https://ru.wikipedia.org (Дата обращения: 14.04.2019)
Гипербола: определение, свойства, построение// Математический форум Math Help Planet: [http://mathhelpplanet.com/static.php]. – Режим доступа: http://mathhelpplanet.com/static.php?p=giperbola (Дата обращения: 14.04.2019)
Гиперболоид//Википедия: [https://ru.wikipedia.org]. – Режим доступа: https://ru.wikipedia.org (Дата обращения: 14.04.2019)
История изучения геометрического тела конус //UZTEST.RU: [http://uztest.ru/]. – Режим доступа: http://uztest.ru/abstracts/?idabstract=523545 (Дата обращения: 14.04.2019)
Коническое сечение//Википедия: [https://ru.wikipedia.org]. – Режим доступа: https://ru.wikipedia.org (Дата обращения: 14.04.2019)
Конус//Википедия: [https://ru.wikipedia.org]. – Режим доступа: https://ru.wikipedia.org (Дата обращения: 14.04.2019)
Кривая второго порядка//Википедия: [https://ru.wikipedia.org]. – Режим доступа: https://ru.wikipedia.org (Дата обращения: 14.04.2019)