Корпускулярная и континуальная концепции описания природы

Корпускулярная
концепция
Концепция атомизма: поиск «элементарных не делимых кирпичиков» мироздания - атомов.

Континуальная
концепция
Материя непрерывна и бесконечно делима

Дискретность (корпускулярность) и
непрерывность (континуальность)
материи
Демокрит –материя состоит из атомов.
Аристотель – материя непрерывна.
Ньютон – свет это частицы.
Гюйгенс – свет это волны.
Классическая физика – поле непрерывно, а вещество дискретно.
Квантовая физика – поля и микрочастицы обладают свойствами непрерывности и дискретности.

Поле и вещество.

Концепции дальнодействия и близкодействия
После работ Ньютона и триумфа закона тяготения утвердилось представление о том, что взаимодействие между телами осуществляется непосредственно через пустое пространство, причем происходит мгновенно. Например считалось, что перемещение Земли должно сразу же приводить к изменению силы тяготения, действующей на Луну. В этом состояла так называемая концепция дальнодействия.

После открытия и исследования электромагнитного поля эти представления были повержены. Скорость распространения электромагнитного поля равна скорости света (в вакууме – 3⋅108 м/с).
Любое взаимодействие не может передаваться со скоростью большей, чем скорость света.
Возникла новая концепция – близкодействия, которая затем была распространена на любые другие взаимодействия. Согласно этой концепции взаимодействие между частицами осуществляется посредством тех или иных полей, скорость распространения которых в пространстве не может быть больше скорости света.

Гравитационное
Электромагнитное
Поле ядерных сил или поле
сильного взаимодействия
Поле слабого взаимодействия
Действуют в пределах ядра
Поле ядерных сил ответственно за взаимодействие нуклонов в ядре, а поле слабого взаимодействия обуславливает некоторые виды ядерных распадов элементарных частиц.
Виды полей и радиус их действия
Rд = ∞
Rд ≈ 10-15
Rд ≈ 10-18

Эти поля ответственны за все взаимодействия в природе и поэтому эти 4 взаимодействия назвали фундаментальными
В классической физике поле и вещество противопоставляются друг другу как два вида материи, качественно отличающихся друг от друга. Но эти формы материи равноценны, т.к. для тех и других выполняются такие общие законы природы, как закон сохранения энергии и т. д.
Различие между этими двумя формами материи не абсолютно. Квантовая физика внесла идею о двойственной корпускулярно-волновой природе любого микрообъекта и показала взаимосвязь этих форм материи. Так микрочастицы могут проявлять волновые свойства, а поля корпускулярные.

Электростатическое поле

Электрический заряд
В природе существует только два типа заряда -положительный и отрицательный
Заряд дискретен – заряд любого тела составляет целое кратное от элементарного заряда:
± e = 1,6⋅ 10-19 Кл
Носители элементарных зарядов:
Электрон (me =9,11 ⋅ 10-31 кг )
Протон (mp =9,11 ⋅ 10-27 кг )

В замкнутой (не обменивающейся зарядами с внешними телами) системе алгебраическая сумма зарядов всех тел остается постоянной:
Закон сохранения электрического заряда

Электрическое поле в вакууме
Электрическое взаимодействие, закон Кулона.
Напряженность электростатического поля.
Принцип суперпозиции полей.
Теорема Гаусса
Потенциал электростатического поля.

Закон Кулона
Закон взаимодействия точечных неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.

Закон Кулона
Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними

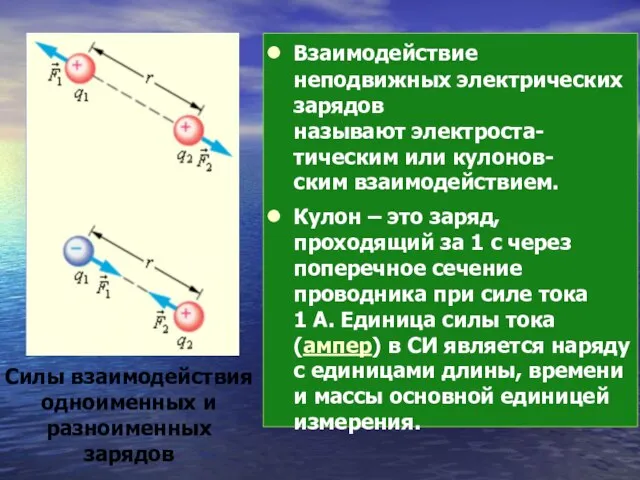
Взаимодействие неподвижных электрических зарядов называют электроста-тическим или кулонов-ским взаимодействием.
Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.
Силы взаимодействия
одноименных и
разноименных
зарядов

Коэффициент k в системе СИ
обычно записывают в виде:
тогда
ε0 = 8,85⋅10-12 Кл2/(Н⋅м2), или
ε0 = 8,85⋅10-12 Ф/м,
где Ф [фарад – единица электроемкости]
ε0 -электрическая постоянная.
= 9⋅109 м/Ф

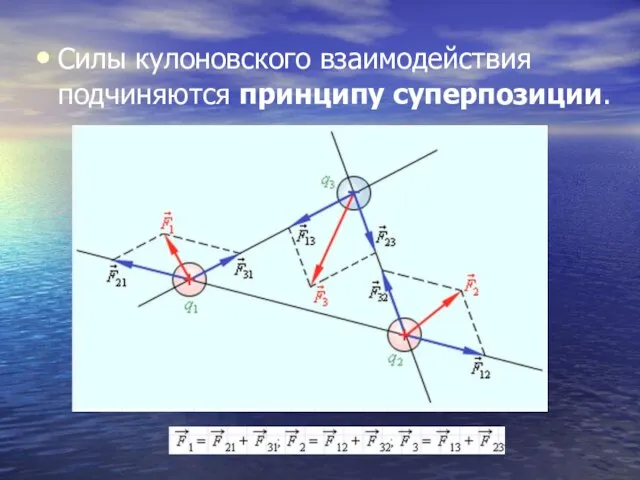
Силы кулоновского взаимодействия подчиняются принципу суперпозиции.

Электростатическое поле.
Электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электростатическое поле.
Поле, окружающее заряженное тело, исследуют с помощью так называемого пробного заряда – небольшого по величине положительного точечного заряда, который не производит заметного перераспределения исследуемых зарядов.

Напряженность электростатического поля
Для количественного определения электрического поля водится силовая характеристика напряженность электростатического поля.
Напряженностью электростатического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда:
Напряженность точечного заряда Q
в вакууме
Напряженность
вектор

Единица напряженности –ньютон на кулон (Н/К)
1 Н/К = 1 В/м, где В (вольт) – единица потенциала электростатического поля.
Электростатическое поле подчиняется принципу суперпозиции:
напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:

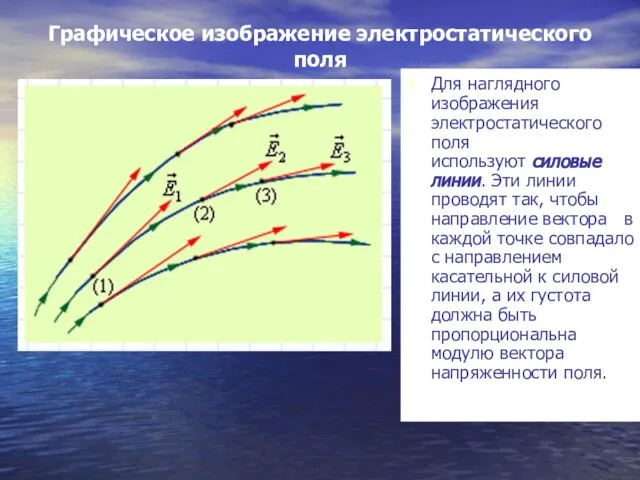
Графическое изображение электростатического поля
Для наглядного изображения электростатического поля используют силовые линии. Эти линии проводят так, чтобы направление вектора в каждой точке совпадало с направлением касательной к силовой линии, а их густота должна быть пропорциональна модулю вектора напряженности поля.

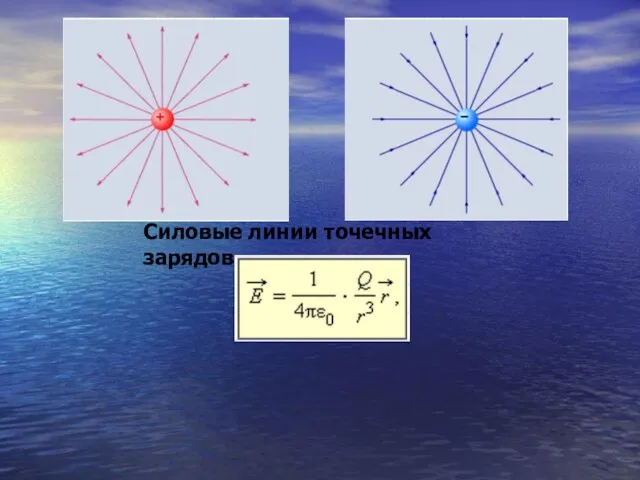
Силовые линии точечных зарядов

Силовые линии двух разноименных зарядов

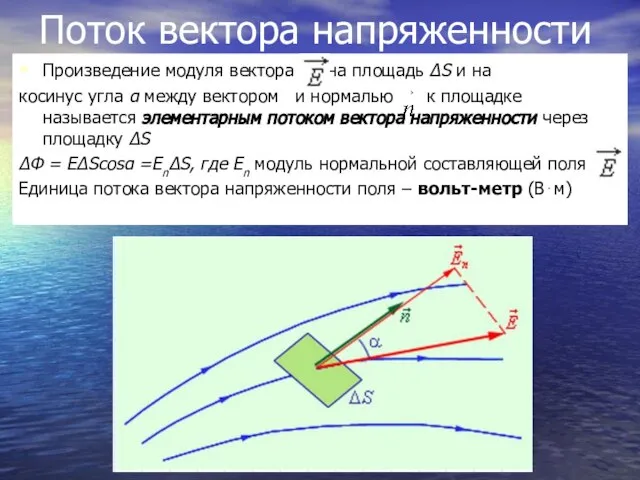
Поток вектора напряженности
Произведение модуля вектора на площадь ΔS и на
косинус угла α между вектором и нормалью к площадке называется элементарным потоком вектора напряженности через площадку ΔS
ΔΦ = EΔScosα =EnΔS, где En модуль нормальной составляющей поля
Единица потока вектора напряженности поля – вольт-метр (В⋅м)

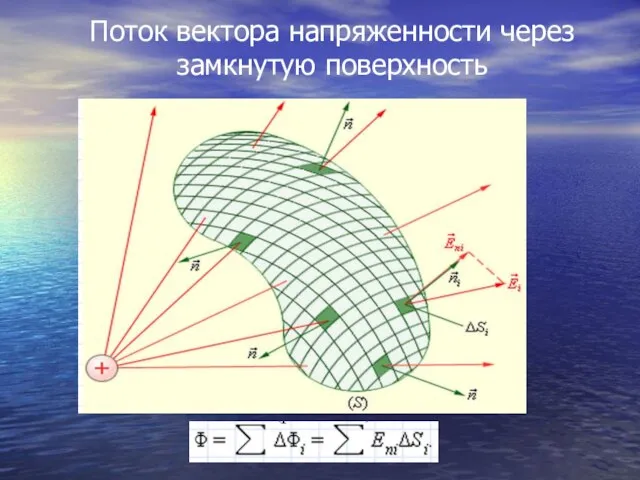
Поток вектора напряженности через замкнутую поверхность

Теорема Гаусса
Теорема Гаусса утверждает:
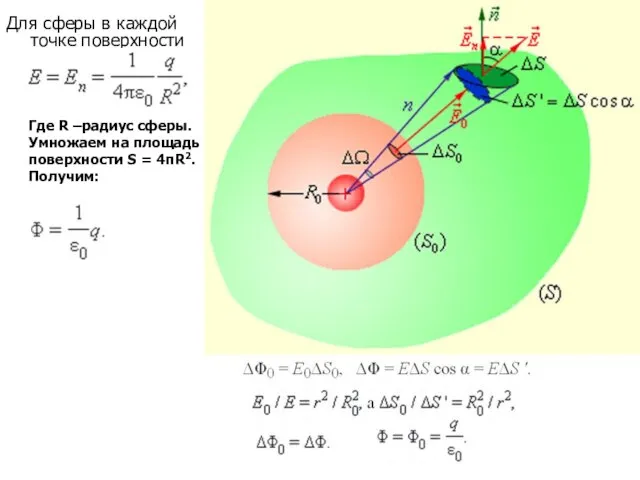
Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.

Для сферы в каждой точке поверхности
Где R –радиус сферы.
Умножаем на площадь
поверхности S = 4πR2.
Получим:

Использование теоремы Гаусса для вычисления напряженности электростатического поля

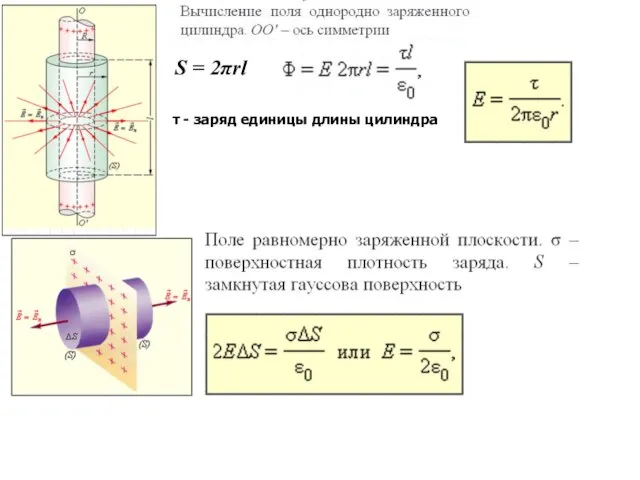
S = 2πrl
τ - заряд единицы длины цилиндра

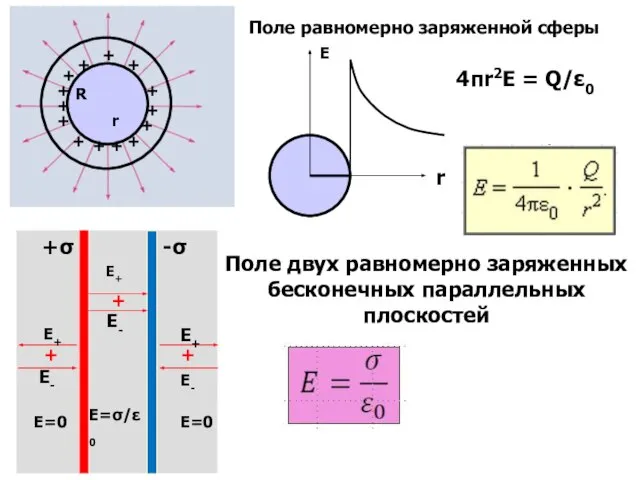
Поле равномерно заряженной сферы
4πr2E = Q/ε0
Поле двух равномерно заряженных бесконечных параллельных
плоскостей

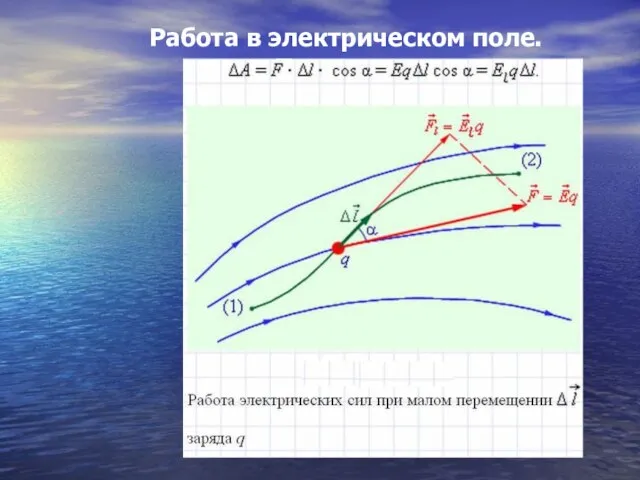
Работа в электрическом поле. Потенциал

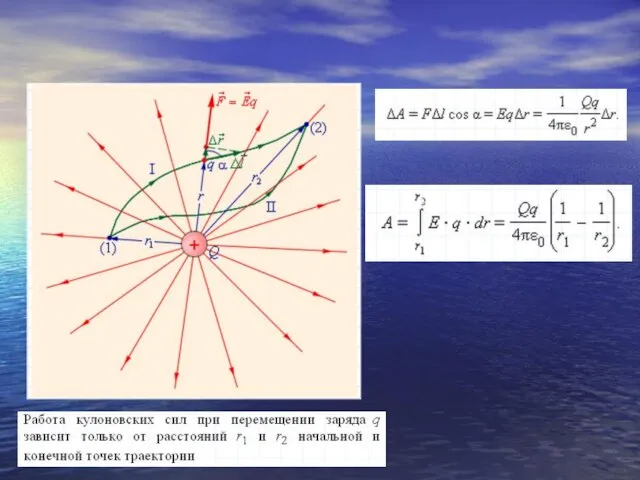
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Следствием независимости работы от формы траектории является следующее утверждение:
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.

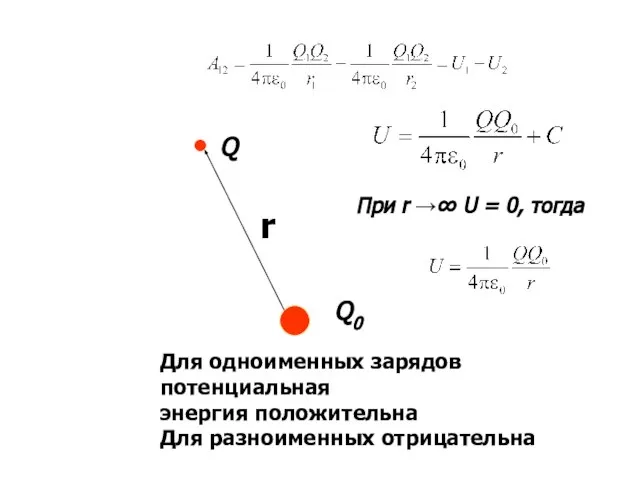
Потенциальная энергия заряда в электрическом поле.
Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.

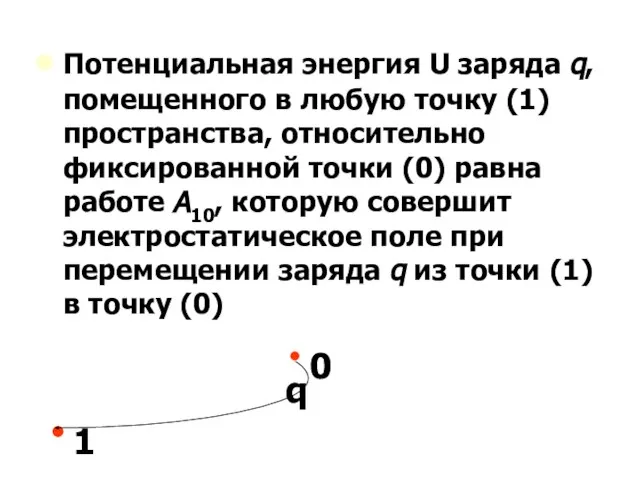
Потенциальная энергия U заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A10, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0)
0
1
q

При r →∞ U = 0, тогда
Для одноименных зарядов потенциальная
энергия положительна
Для разноименных отрицательна

Потенциал φ электростатического поля
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электростатического поля:
ϕ = U/Q

Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
В Международной системе единиц (СИ) единицей потенциала является вольт (В). 1 В = 1 Дж / 1 Кл.

Эквипотенциальные поверхности.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.

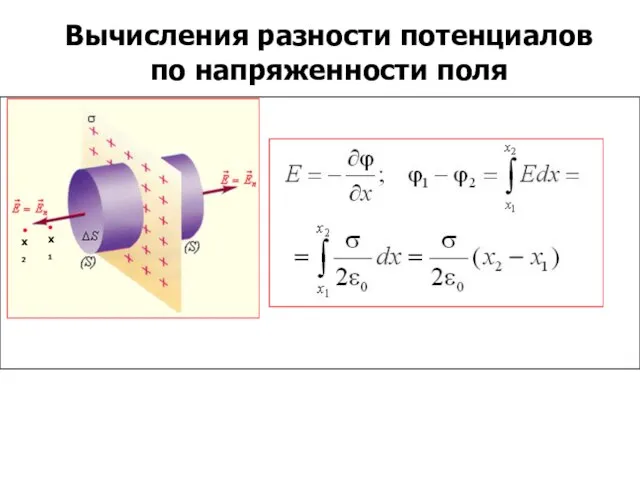
Связь между напряженностью поля и потенциалом.
Если пробный заряд q совершил малое перемещение вдоль силовой линии из точки (1) в точку (2), то можно записать:
ΔA12 = qEΔl = q(φ1 – φ2) = – qΔφ,
где Δφ = φ1 – φ2 – изменение потенциала

Напряженность как градиент потенциала
где
единичные векторы
координатных осей x,y,z
Знак «-» означает, что поле направлено в сторону
Убывания потенциала

Вычисления разности потенциалов по напряженности поля
x2
x1

Единица электроемкости
Единица электроемкости – фарад (Ф)
1 Ф – емкость такого уединенного проводника потенциал которого меняется на 1 В при сообщении ему заряда 1 Кл.
Из этого следует, что емкостью в 1 Ф обладал бы уединенный шар, в вакууме и имеющий радиус R = C/(4πε0) ≈9⋅106 км.
Электроемкость Земли C ≈ 0,7 Ф

Конденсаторы
Если двум изолированным друг от друга проводникам сообщить заряды q1 и q2, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников. Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U.

Электроемкостью системы из двух проводников имеющих одинаковые, но противоположные по знаку заряды называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, – обкладками.
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским.

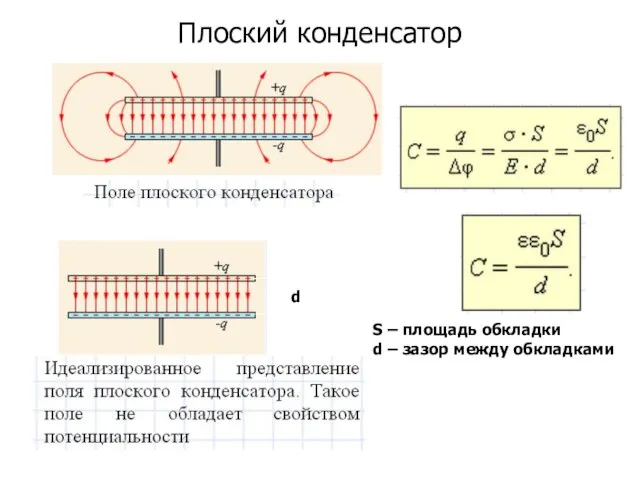
Плоский конденсатор
d
S – площадь обкладки
d – зазор между обкладками

Емкости сферического и цилиндрического конденсаторов
Сферический конденсатор – это система из двух концентрических проводящих сфер радиусов R1 и R2. Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R1 и R2 и длины L.

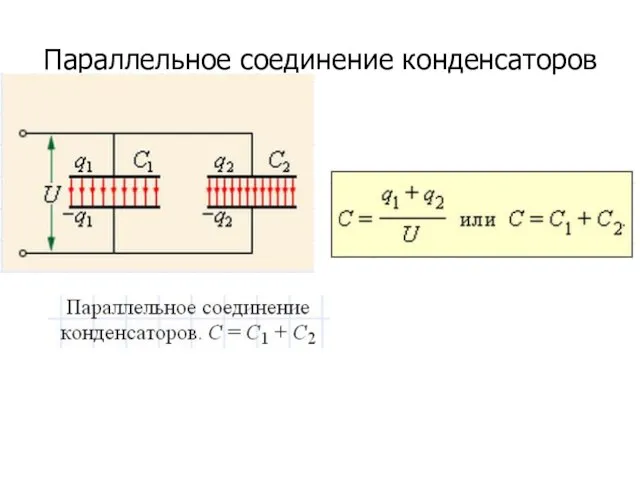
Параллельное соединение конденсаторов

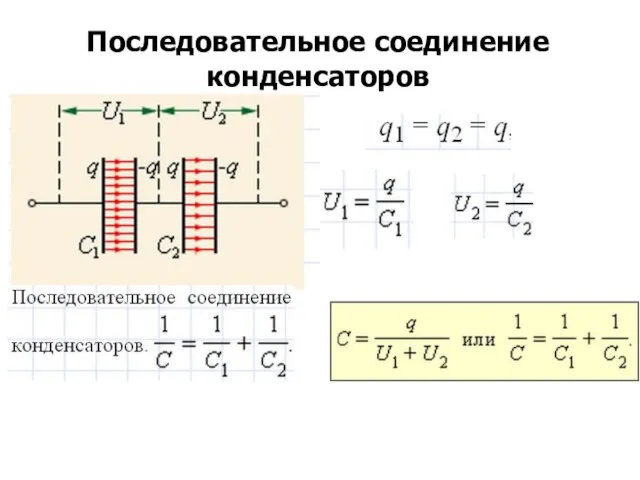
Последовательное соединение конденсаторов

Энергия системы зарядов, уединенного проводника, конденсатора, электрического поля.
Энергия системы зарядов
Где ϕi –потенциал создаваемый в точке, где находиться заряд Qi, всеми зарядами, кроме i – го.

Энергия заряженного уединенного проводника
Энергия заряженного проводника равна той работе, которую надо совершить, чтобы зарядить этот проводник:
dA=ϕdQ =Cϕdϕ

Энергия заряженного конденсатора

Сила, с которой обкладки конденсатора притягиваются друг к другу
dA =Fdx = - dW
x
x

Энергия электростатического поля
Δϕ = Ed
Подставим эти выражения в формулу энергии конденсатора
Объемная плотность энергии электростатического поля

Волновое движение и его свойства
Волны – это изменение состояния среды (возмущение), распространяющееся в этой среде и несущее с собой энергию и импульс без переноса вещества.
Наиболее часто встречающиеся виды волн – упругие (звук) и электромагнитные (свет, радиоволны и другие).

Для описания волнового движения используется уравнение распространения гармонических колебаний в пространстве, например, вдоль координаты x:
A = A0cos(ωt + kx).
оно называется уравнением бегущей одномерной синусоидальной (гармонической) волны.
В нем:
A0 – амплитуда колебаний;
ω – круговая частота (рад/с);
k = ω/υ - волновое число
υ – скорость распространения волны м/с).
период колебаний T (с), который связан с круговой частотой соотношением: T = 2π/ω;

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Следствием независимости работы от формы траектории является следующее утверждение:
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.

Наиболее часто используемыми характеристиками волнового движения являются:
γ - частота колебаний (Гц=1/с) . Она связана с периодом формулой: γ = 1/T;
λ – длина волны (м). (λ = υT).
υ – скорость распространения волны м/с).
Скорость распространения каждого вида волн зависит только от свойств среды, в которой они распространяются.
Например скорость звука в воздухе не зависит от длины волны (υ ~ 343 м/с). В воде она порядка 1500 м/с

По характеру колебаний волны подразделяются на:
поперечные - колебания совершаются поперек направления их распространения (свет).
продольные - колебания совершаются вдоль направления их распространения (звук).
поверхностные - распространяются вдоль границы раздела двух сред, например, на поверхности воды, и частицы жидкости движутся почти по окружности, т. е. они представляют собой комбинацию поперечных и продольных волн.
Кроме бегущих волн существуют так называемые стоячие волны, которые можно рассматривать как результат сложения двух бегущих волн. В определенных условиях, в результате такого сложения, амплитуда колебаний в каждой точке пространства перестает зависеть от времени. В зависимости от x ее величина, будет разная (от 0 до A0 ).

Свойства волнового движения
При не очень больших возмущениях среды волновые процессы подчиняются принципу суперпозиции (принципу наложения). То есть результирующий эффект сложного процесса воздействия представляет собой сумму эффектов, вызываемых каждым воздействием в отдельности. Согласно этому принципу, две волны могут распространяться в той же самой среде в разных направлениях совершенно независимо друг от друга. Принципу суперпозиции подчиняются как волны в упругой среде, так и электромагнитные волны.

Дифракция
Проникновение волны в область геометрической тени называют дифракцией. Чем меньше ширина преграды и чем больше длина волны, тем сильнее проявляется дифракция.

Интерференция волн
Явление ослабления или усиления волнового движения в результате суперпозиции когерентных волн называется интерференцией.
Когерентными называются волны одинаковой частоты, если их разность фаз не зависит от времени.

Эффект Доплера
Эффект Доплера заключается в изменении принимаемой приемником частоты (или длины) волны в зависимости от движения источника (или приемника) излучения.

Электромагнитные волны
Все окружающее нас пространство пронизано электромагнитными волнами. Солнце и окружающие нас тела, радиоантенны и далекие звезды испускают электромагнитные волны, которые в зависимости от длины волны носят разные названия: радиоволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновское излучение и γ-излучение.

Электромагнитные волны, независимо от длины волны, возникают из-за ускоренного движения заряженных частиц.