Корреляционный анализ

Понятие корреляции отражает, главным образом, степень выраженности связи между переменными.
Регрессионный анализ отвечал на вопрос: Каков характер связи между признаками (прямолинейный, криволинейный, какой функцией эту связь можно описать).
Корреляционный анализ отвечает на вопрос: Какова сила связи между признаками.
Понятие корреляции

Одним из подходов к корреляции является вычисление доли объясняемой дисперсии, т.е. доли вариабельности одного признака, зависящей от вариабельности другого.
Эта мера вычисляется по формуле: r2 × 100(%) (где r - коэфф. кор-реляции.)
Например, для коэффициента корреляции r=0,5, доля объясняемой дисперсии равна 0,52 × 100(%) = 25%
Понятие корреляции

Коэффициент корреляции показывает, в какой степени изменение значения одного признака сопровождается изменением значения другого признака.
Основной носитель информации о корреляции - коэффициент корреляции (r)
Значения коэффициента корреляции изменяются в интервалах от 1 до -1.
Крайние значения (±1) указывают на наличие линейной функциональной связи между признаками.
Ноль - на отсутствие статистической связи.
Понятие коэффициента корреляции

По направлению, связь может быть прямой и обратной, а по силе – сильной, средней и слабой. Узнать эти свойства связи позволяет коэффициент корреляции:
Оценка связи по силе и направлению

Коэффициент корреляции вычисляют двумя способами:
1) Параметрический метод Пирсона (20% биомед.данных)
!Критерий согласия!
2) Непараметрические методы: ранговой корреляции Спирмена, метод Кендалла, гамма и проч.
Формула коэффициента корреляции Пирсона (параметрический)
Формула коэффициента корреляции Спирмена (Ранговый, непараметрический)

Алгоритм работы с коэффициентом корреляции
1. Определение распределения данных (критерий согласия). Выбор адекватного методы вычисления к.к.
2. Вычисление коэффициента корреляции
3. Проверка статистической гипотезы о значимости коэффициента корреляции (по критерию Стьюдента)
4. Вывод о силе, направлении и достоверности связи между признаками.

1. Определение распределения данных
(критерий согласия)
Если данные распределены нормально, то к ним применим параметрический метод Пирсона.
Если признаки или хотя бы один из них распределен не нормально, допустимо применение только непараметрических ранговых методов (Спирмена, Кендалла, Гамма и др.).
Проверка гипотезы о виде распределения (критерия согласия) Колмогорова-Смирнова, Лилефорса, Шапиро-Вилка.
H0 критерия согласия: Признак распределен нормально
H1 критерия согласия: Признак распределен не нормально
Проверка по каждому признаку!

2. Вычисление коэффициента корреляции
А) Метод Пирсона. См. учебник
Б) Метод Спирмена:
Правила присваивания рангов
Ранг наблюдения – номер, который получит наблюдение в совокупности после ранжирования (по определенному правилу).
Если отдельные наблюдения встречаются в ряду несколько раз, то каждому из них присваивается одинаковый ранг, равный среднему рангу.
Коэффициент ранговой корреляции Спирмена вычисляется (d-разность рангов):

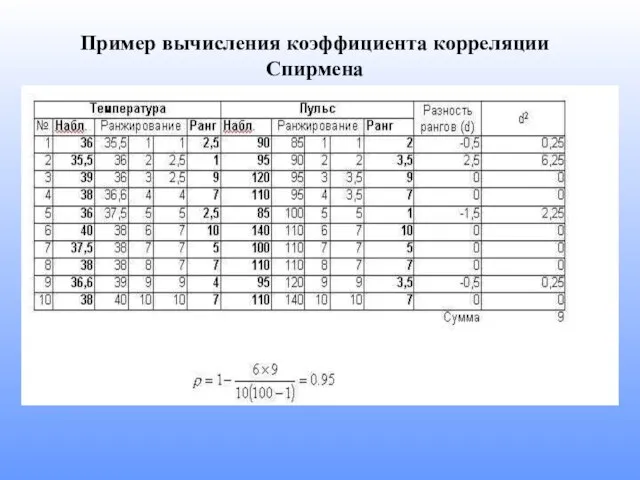
Пример вычисления коэффициента корреляции Спирмена

3. Проверка статистической гипотезы о значимости коэффициента корреляции (по критерию Стьюдента)
1. Формулировка гипотез:
H0: Коэффициент корреляции не достоверен (r = 0)
H1: Коэффициент корреляции достоверен (r ≠ 0)
2. Уровень значимости (α=0,05)
3. Работа с критерием Стьюдента
3.1 Вручную
3.2 В программа СА. P-level
4. Вывод: p> α Нет оснований отвергать H0
p< α отвергаем H0,, принимаем H1
t крит=табл. Критические точки t-критерия Стьюдента (Альфа и n-2 степеней свободы)

4. Вывод о силе, направлении и достоверности связи между признаками.
1. Оценка направления связи - по знаку к.к.
2. Оценка силы связи - по значению к.к.
3. Оценка достоверности связи - сравнение p и α
Пример: r = 0.39 p = 0.4; r = 0.97 p = 0.04; r = -0.23 p = 0.001