Круги Эйлера

Цель исследования:
изучение биографии Л. Эйлера
изучение способа решения задач с помощью кругов Эйлера;
Задачи исследования:
Познакомится с кругами Эйлера, кругами (диаграммами) Эйлера – Венна.
Составлять и решать подобные задачи

Биография Леонарда Эйлера
Леона́рд Э́йлер (15) апреля 1707, Базель, Швейцария — 7 (18) сентября
1783, Санкт-Петербург, Российская империя) — российский и швейцарский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.

Почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. В 1726 году он был приглашён работать в Санкт-Петербург. В 1731—1741 и, начиная с 1766 года, был академиком Петербургской Академии Наук (в 1741—1766 годах работал в Берлине, оставаясь почётным членом Петербургской Академии). Хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском.

Типы кругов Эйлера
Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.

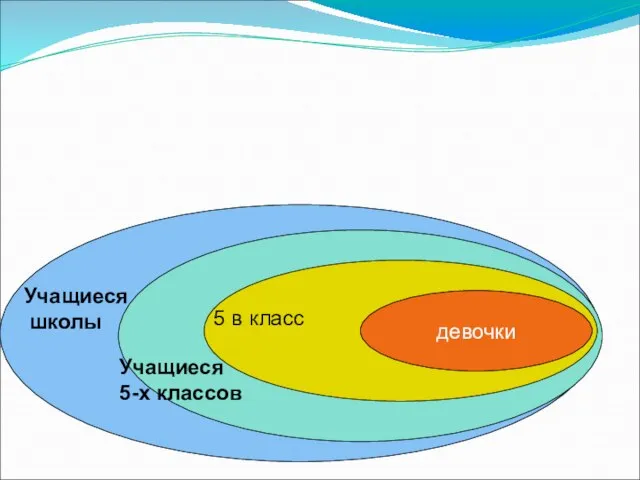
Учащиеся
школы
Учащиеся
5-х классов
5 в класс
девочки

Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?
2
3
4
ОТВЕТ : 9 ПОДРУГ
Кактусы
фиалки
кф
Задача №1

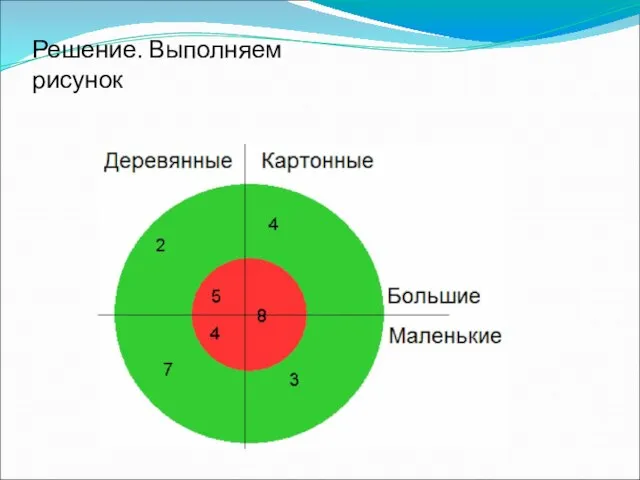
Задача, решаемая с помощью диаграммы Эйлера – Венна.
Ребятам поручили изготовить кубики. Несколько кубиков сделали из картона, а остальные из дерева. Кубики были двух размеров: большие и маленькие. Часть из них покрасили в зеленый цвет, другую – в красный. Получилось 16 зеленых кубиков. Зеленых кубиков большого размера было 6. Больших зеленых из картона было 4. Красных кубиков из картона было 8,красных кубиков из дерева – 9. Больших деревянных кубиков было 7, а маленьких деревянных кубиков было 11. Сколько же всего получилось кубиков?
Задача №2

Решение. Выполняем рисунок

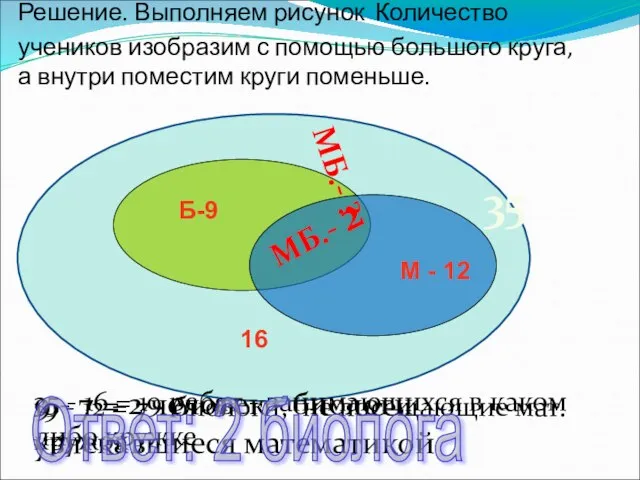
Задача №3
В классе 35 учеников. В математическом кружке из них 12 занимаются, в биологическом - 9, а 16 ребят не посещают эти кружки. Сколько биологов увлекаются математикой.

35
35 - 16 = 19 ребят - занимающихся в каком либо кружке
19 - 12 = 7 - биологи, не посещающие мат. кружок
9 - 7 = 2 человек - биологи увлекавшиеся математикой
Решение. Выполняем рисунок Количество учеников изобразим с помощью большого круга, а внутри поместим круги поменьше.
16
Б-9
М - 12
МБ.- ?
МБ.- 2
Ответ: 2 биолога

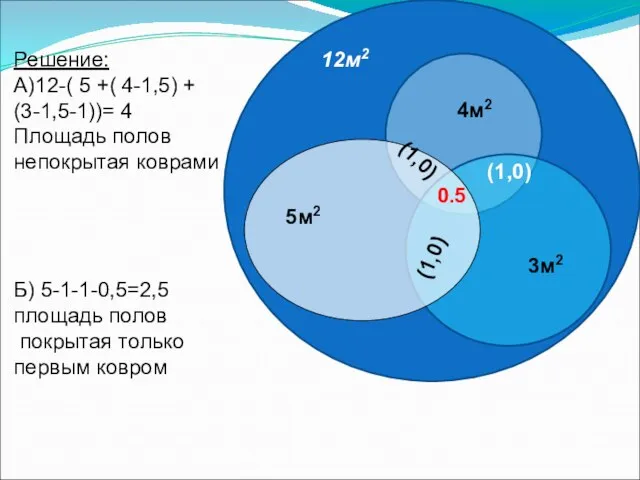
На полу площадью 12м2 лежат три ковра: площадь одного 5м2, другого - 4м2 и третьего - 3м2. Каждые два ковра перекрываются на площади 1,5м2, причем 0,5м2 из этих полутора квадратных метров приходится на участок пола, где перекрываются все три ковра. а) Какова площадь пола, не покрытая коврами? б) Какова площадь пола, покрытая одним только первым ковром?
Задача №4

Решение:
А)12-( 5 +( 4-1,5) + (3-1,5-1))= 4
Площадь полов
непокрытая коврами
Б) 5-1-1-0,5=2,5 площадь полов
покрытая только первым ковром

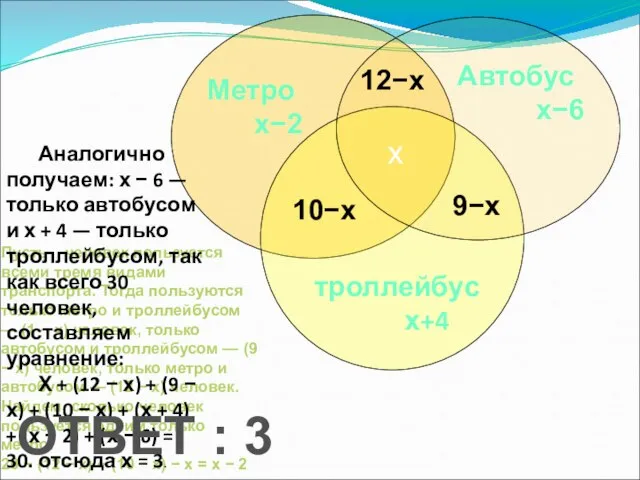
Всего – 30 человек
Пользуются метро – 20 человек
Автобусом – 15 человек
Троллейбусом – 23 человека
Метро и троллейбусом – 10 человек
Метро и автобусом – 12 человек
Троллейбусом и автобусом – 9
Сколько человек ежедневно пользуются всеми тремя видами транспорта?
Задача №6

троллейбус
х+4
Автобус
х−6
Метро
х−2
х
10−х
9−х
12−х
Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (1 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро:
20 − (12 − х) − (10 − х) − х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3.
ОТВЕТ : 3

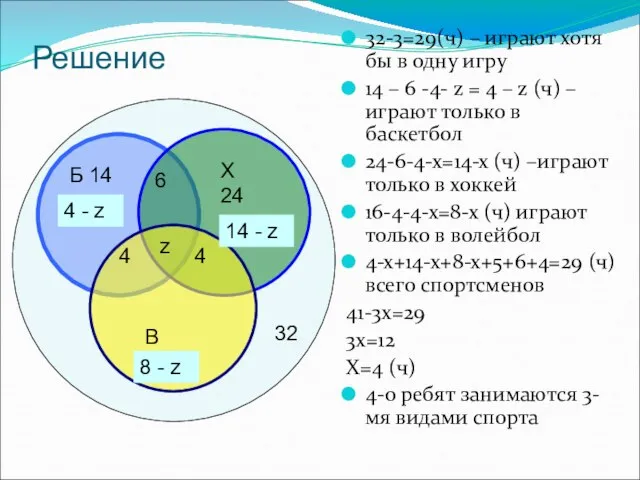
Всего- 32 чел
Баскетбол - 16 чел
Хоккей - 24 чел
Волейбол - 16 чел
Б.Х - 6 чел
Б.В - 4 чел
В.Х - 4 чел
Ни чем– 3 чел
Сколько человек занимаются всеми видами спорта? В одной спортивной секции?
Задача №5

Решение
32-3=29(ч) – играют хотя бы в одну игру
14 – 6 -4- z = 4 – z (ч) –играют только в баскетбол
24-6-4-х=14-х (ч) –играют только в хоккей
16-4-4-х=8-х (ч) играют только в волейбол
4-х+14-х+8-х+5+6+4=29 (ч) всего спортсменов
41-3х=29
3х=12
Х=4 (ч)
4-о ребят занимаются 3-мя видами спорта
Б 14
4 - z
Х 24
14 - z
В 16
8 - z
6
z
4
4
32

заключение
Ты человек, а значит, ты
Обязан рассуждать –
А без логичной простоты
Ты будешь пропадать.
Пусть за собой она зовёт –
Уйми в коленях дрожь!
Коль с Логикой пойдёшь вперёд –
Нигде не пропадёшь!
(С. Алдошин)

Выводы
Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.

Выводы:
Для решения задач, решаемых с помощью кругов Эйлера, был составлен алгоритм, состоящий из следующих этапов:
Записываем краткое условие задачи.
Выполняем рисунок.
Записываем данные в круги (или в диаграмму Эйлера).
Выбираем условие, которое содержит больше свойств.
Анализируем, рассуждаем, не забывая записывать результаты в части круга (диаграммы).
Записываем ответ.