Круги Эйлера в решении задач

Леонард Эйлер
Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал в Россию. Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира.
Одним из первых, кто использовал для решения задач круги, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с кругами. Затем этот метод основательно развил швейцарский математик Леонард Эйлер (1707 – 1783).
(1707 г.-1783 г.)

С1761 по 1768 год им были написаны знаменитые «Письма к немецкой принцессе», где Эйлер как раз и рассказывал о своем методе, об изображении множеств в виде кругов. Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения». Понятно, что слово «круг» здесь весьма условно, множества могут изображаться на плоскости в виде произвольных фигур.

После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841 – 1902). Этот метод широко используется в его книге «Алгебра логика». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.

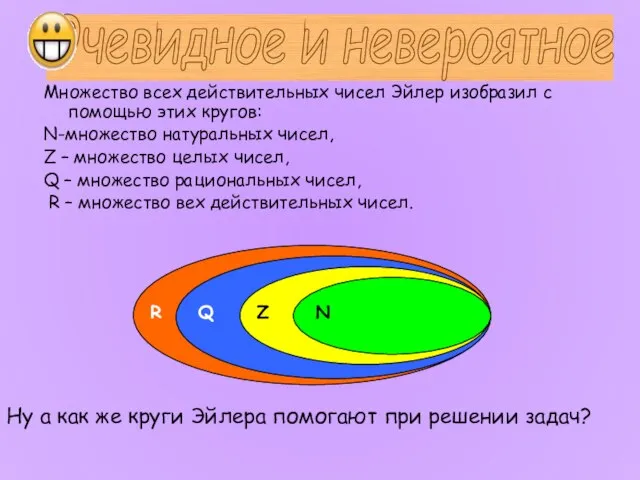
Множество всех действительных чисел Эйлер изобразил с помощью этих кругов:
N-множество натуральных чисел,
Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество вех действительных чисел.
Очевидное и невероятное
Ну а как же круги Эйлера помогают при решении задач?
R
Q
Z
N

Круги Эйлера
Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.

Круги ЭЙЛЕРА — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.

Типы кругов Эйлера

Решение задач
"Обитаемый остров" и "Стиляги"
Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Решение
Чертим два множества таким образом:
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.
15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».
11 – 6 = 5 – человек, которые смотрели только «Стиляги».
Получаем:
Ответ. 5 человек смотрели только «Стиляги».
6
«обитаемый остров»
«Стиляги»
«обитаемый остров»
«Стиляги»
9
6
5

«Мир музыки»
В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?
Решение
Изобразим эти множества на кругах Эйлера.

Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно, 25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры:
Ответ: 6 покупателей купили диски и Максим, и Земфиры.

Рассмотрение простейших случаев кругов Эйлера – Венна
а) Пусть дано некоторое множество и указано свойство А. Очевидно, элементы данного множества могут обладать или не обладать данным свойством. Поэтому данное множество распадается на две части, которые можно обозначить через А и А*. На рисунке можно это изобразить двумя способами.
Большой круг изображает данное множество, маленький круг А – ту часть элементов данного множества, которое обладает свойством А, а кольцеобразная часть А* – ту часть элементов, которые не обладают свойством А.

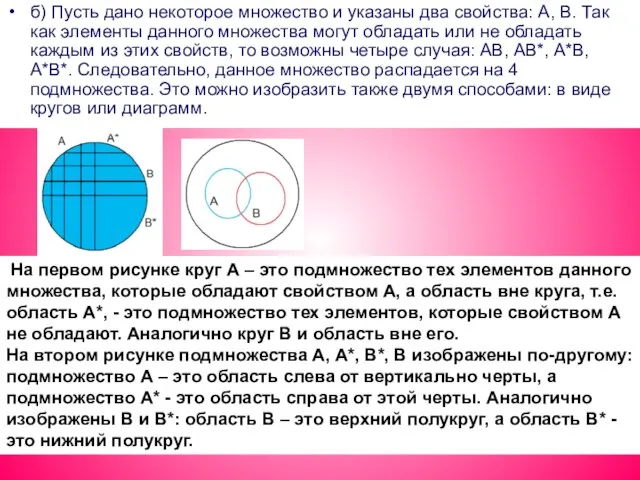
б) Пусть дано некоторое множество и указаны два свойства: А, В. Так как элементы данного множества могут обладать или не обладать каждым из этих свойств, то возможны четыре случая: АВ, АВ*, А*В, А*В*. Следовательно, данное множество распадается на 4 подмножества. Это можно изобразить также двумя способами: в виде кругов или диаграмм.
На первом рисунке круг А – это подмножество тех элементов данного множества, которые обладают свойством А, а область вне круга, т.е. область А*, - это подмножество тех элементов, которые свойством А не обладают. Аналогично круг В и область вне его.
На втором рисунке подмножества А, А*, В*, В изображены по-другому: подмножество А – это область слева от вертикально черты, а подмножество А* - это область справа от этой черты. Аналогично изображены В и В*: область В – это верхний полукруг, а область В* - это нижний полукруг.

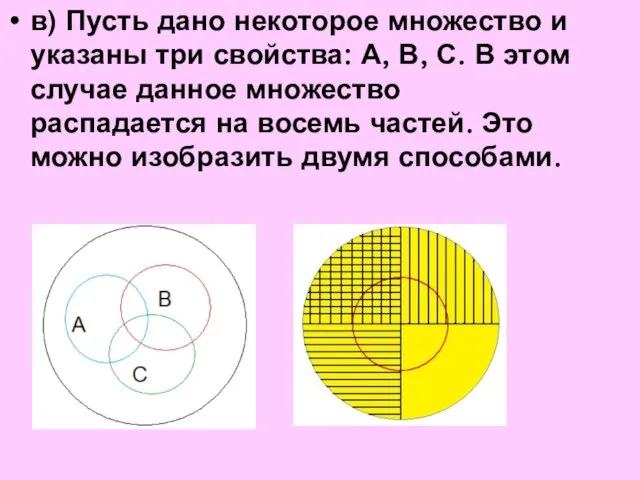
в) Пусть дано некоторое множество и указаны три свойства: А, В, С. В этом случае данное множество распадается на восемь частей. Это можно изобразить двумя способами.

Задачи, решаемые с помощью кругов Эйлера
Задача №1. Сколько натуральных чисел из первого десятка не делится ни на 2, ни на 3?
Решение. Для решения задачи удобно воспользоваться кругами Эйлера. В нашем случае три круга: большой круг – это множество чисел от 1 до 10, внутри большого – два меньших круга, пресекающихся друг с другом. Пусть множество чисел, кратных 2– это множество А, а множество чисел, кратных 3 – множество В. Рассуждаем. На 2 делится каждое второе число. Значит, таких чисел будет 10:2=5. На 3 делится 3 числа (10:3). На 2 и 3 делятся те числа, которые делятся на 6. Такое число только одно. Поэтому множество А состоит из 5-1=4 чисел, множество В – 3-1=2 чисел. Отсюда следует, что в первом десятке содержится 10-(4+1+2)=3 числа.

Задача № 2. Задача, решаемая с помощью диаграммы Эйлера – Венна.
Ребятам поручили изготовить кубики. Несколько кубиков сделали из картона, а остальные из дерева. Кубики были двух размеров: большие и маленькие. Часть из них покрасили в зеленый цвет, другую – в красный. Получилось 16 зеленых кубиков. Зеленых кубиков большого размера было 6. Больших зеленых из картона было 4. Красных кубиков из картона было 8,красных кубиков из дерева – 9. Больших деревянных кубиков было 7, а маленьких деревянных кубиков было 11. Сколько же всего получилось кубиков?
Решение. Выполняем рисунок.

Составление задач, имеющих практическое значение.
Задача 1. В классе 35 учеников. В математическом кружке из них 12 занимаются, в биологическом - 9, а 16 ребят не посещают эти кружки. Сколько биологов увлекаются математикой.
Решение: Мы видим, что кружки посещают 19 ребят, так как 35 - 16=19, из них 10 человек посещают только математический кружок (19-9=10) и 2 биолога (12-10=2) увлекаются математикой.
Ответ: 2 биолога.
С помощью кругов Эйлера легко увидеть и другой способ решения задачи.
Количество учеников изобразим с помощью большого круга, а внутри поместим круги поменьше.
Очевидно, что в общей части кругов окажутся те самые биологи-математики, о которых спрашивается в задаче. Теперь посчитаем: Внутри большого круга 35 учеников, внутри кругов М и Б : 35-16=19 учеников, внутри круга М - 12 ребят, значит, в той части круга Б, которая не имеет ничего общего с кругом М, находится 19-12=7 учеников, следовательно, в МБ находится 2 ученика (9-7=2). Таким образом, 2 биолога увлекаются математикой.
1)35-16=19(чел.);
2) 12+9=21 (чел.);
3)21-19=2(чел.).
Ответ: 2 биолога.

Заполняем диаграмму.
1) Надо начинать с того подмножества, для которого указаны три свойства. Это большие зеленый кубики из картона – таких кубиков 4.
2) Далее ищем подмножества, для которого указаны два свойства из перечисленных трех. Это большие зеленые кубики – 6. Но это подмножество состоит из картонных и деревянных. Картонных было 4. Значит, деревянных 6-4=2.
3) Больших деревянных кубиков 7. Из них зеленых – 2. Значит, красных будет 7-2=5.
4) Красных деревянных кубиков 9., из них 5 – большие. Значит, маленьких красных кубиков из дерева будет 9-5=4.
5) Маленьких деревянных кубиков 11. Из них красных – 4. Значит, маленьких зеленых кубиков из дерева 11-4=7.
6) Всего зеленых кубиков 16. Зеленые кубики помещены в кольцеобразную часть, состоящую из четырех частей. Значит, маленьких зеленых кубиков из картона 16-(4+2+7)=3.
7) Осталось последнее условии: красных кубиков из картона было 8. Нам и не надо узнать, сколько из них маленьких, сколько больших.
8) Считаем: 2+5+8+4+4+7+3=33. Ответ: всего было изготовлено 33 кубика.

В результате работы над данной темой я пришла к следующим выводам: 1. Все множества чисел связаны между собой так, что каждое следующее, более объемное, включает в себя предыдущее множество полностью;
2. Любое натуральное число является элементом любого следующего множества.
3. Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.
вывод