Содержание
- 2. ВВЕДЕНИЕ Начертательная геометрия- раздел, изучаемый в 1 семестре по дисциплине «Инженерная и компьютерная графика», служит теоретической
- 5. Центральное и параллельное проецирование Аппарат центрального проецирования (система, обеспечивающая построение проекционного изображения) включает в себя: центр
- 6. Параллельное проецирование и его свойства В аппарат параллельного проецирования входят плоскость проекций П1 и направление проецирования
- 7. Виды проецирования Процесс отображения точек пространственного предмета на плоскость проекций с помощью проецирующих линий называется проецированием.
- 8. ПРОЕКЦИИ ГЕОМЕТРИЧЕСКИХ ЭЛЕМЕНТОВ НА ОРТОГОНАЛЬНОМ ЧЕРТЕЖЕ Метод параллельного проецирования является основным при составлении чертежей зданий и
- 9. Для получения плоского чертежа точки А необходимо повернуть плоскость П1 вокруг оси x по часовой стрелке,
- 10. ПРЯМАЯ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ Способы задания прямой Проекциями двух точек (конечным отрезком). Точкой и
- 11. Принадлежность точки прямой линии. Точка принадлежит прямой, если ее проекции принадлежат соответствующим (одноименным) проекциям прямой. Следом
- 12. Натуральная величина отрезка прямой равна гипотенузе прямоугольного треугольника, одним из катетов которого является проекция прямой, а
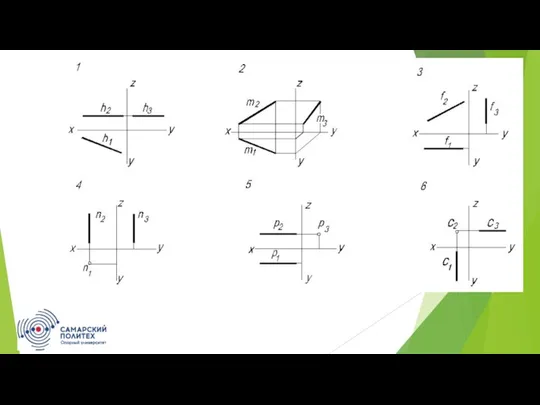
- 13. Прямые частного положения Среди прямых частного положения различают линии уровня и проецирующие прямые. Прямые линии, параллельные
- 14. Профильная прямая p – прямая, параллельная профильной плоскости проекций p || П3 Прямые уровня параллельны одной
- 15. Прямая линия, перпендикулярная одной из плоскостей проекций или параллельная направлению проецирования, называется проецирующей. Рассмотрим проецирующие прямые.
- 16. Профильно-проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций c┴ П3 Проецирующие прямые параллельны двум плоскостям проекций
- 20. Скачать презентацию
Слайд 2ВВЕДЕНИЕ
Начертательная геометрия- раздел, изучаемый в 1 семестре по дисциплине «Инженерная и компьютерная
ВВЕДЕНИЕ
Начертательная геометрия- раздел, изучаемый в 1 семестре по дисциплине «Инженерная и компьютерная

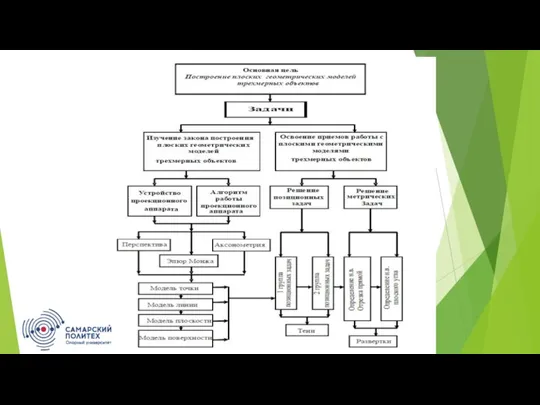
Позиционными называются задачи на взаимную принадлежность и пересечение геометрических фигур принадлежность точки прямой, плоскости или поверхности (принадлежность прямой плоскости; взаимное положение прямой и плоскости; взаимное положение плоскостей; взаимное положение прямой или плоскости с поверхностью; взаимное положение поверхностей); метрическими – задачи на определение расстояний и натуральных величин геометрических фигур (расстояния от точки до прямой или плоскости; расстояния между двумя параллельными или скрещивающимися прямыми; величины плоской фигуры или двухгранного угла), конструкторскими – задачи на построение геометрических фигур, отвечающих заданным условиям.
Логическая структура учебного курса «Инженерная и компьютерная графика» в 1 семестре изображена на 3 слайде. Она накладывает жесткие требования на методику его освоения, характерной чертой которой является регулярность в контроле качества знаний и максимально возможная индивидуализация обучения. Результатом освоения этого учебного курса является формирование алгоритмического мышления. Гармония образного и логического мышления выгодно отличает инженерную графику от многих других дисциплин технического вуза.
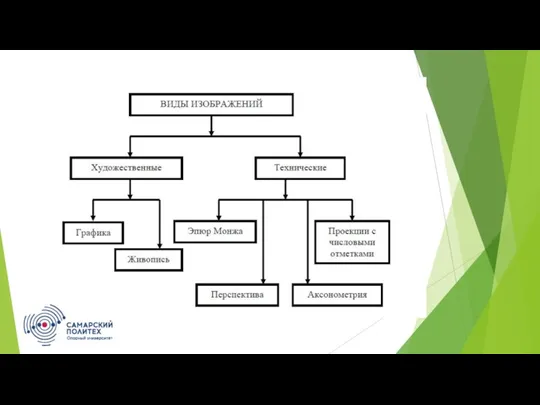
Виды изображений показаны на 4 слайде. Создание художественных изображений называется рисованием или живописью. Его характерной чертой является игнорирование использования специальных инструментов для проведения линий. Процесс создания технических изображений называется черчением, где проведение различных линий требует использования специальных инструментов.
Слайд 5Центральное и параллельное проецирование
Аппарат центрального проецирования (система, обеспечивающая построение проекционного изображения) включает
Центральное и параллельное проецирование
Аппарат центрального проецирования (система, обеспечивающая построение проекционного изображения) включает

(A1, B1, C1, D1 – проекции точек А, В, С, D на плоскость П1; [SA);[SB)… – проецирующие лучи).
Проецирующими элементами называются все прямые и плоскости, проходящие через центр
проекций, а также все конические или пирамидальные поверхности, вершины которых совпадают с
центром проецирования. Точка пересечения проецирующего луча с картинной плоскостью
называется проекцией точки на эту плоскость. Проекция предмета на плоскость – это множество
проекций всех его точек на заданную плоскость.
В общем случае проекцией называется фигура, образовавшаяся от пересечения проецирующего элемента (луча, плоскости или
поверхности) с плоскостью проекций (называемой иногда картинной плоскостью).
Чертеж, кроме передачи формы предмета, должен решать метрическую задачу, т.е. передавать размеры предмета, сооружения. Чертежи, полученные методом центрального проецирования, отличаются большой наглядностью, поскольку построены на том же принципе, что и аппарат человеческого зрения. Однако такие чертежи сложно выполнять и измерять, поскольку размеры предмета искажаются.
Сущность метода параллельного проецирования заключается в следующем: центр проецирования S удаляется в бесконечность, а положение точек пространства и картинной плоскости остается неизменным. Так как центр проецирования удален в бесконечность, проецирующие лучи, проходящие через бесконечно удалённый центр, становятся параллельными. Направление проецирования выбирается произвольно, в зависимости от желаемого результата проецирования. Проецирующими также могут быть любые поверхности – плоскости, линейчатая цилиндрическая или призматическая поверхности, образующие которых параллельны направлению проецирования.
Параллельные проекции подразделяются на косоугольные и прямоугольные (проецирующие лучи располагаются под углом α=900).
Слайд 6 Параллельное проецирование и его свойства
В аппарат параллельного проецирования входят плоскость проекций
Параллельное проецирование и его свойства
В аппарат параллельного проецирования входят плоскость проекций

1. Проекцией точки является точка, проекцией прямой – прямая, проекцией плоской фигуры – фигура ей соответственная. Проекция фигуры на одну плоскость проекций однозначно не определяет пространственного положения объекта.
2. Если точка пространства лежит на прямой, то ее проекция лежит на соответствующей проекции прямой.
3. Если прямые и плоскости совпадают с направлением проецирования, то они сами становятся проецирующими элементами и их проекции вырождаются: прямая проецируется в точку, плоская фигура – в прямую линию.
4. Отношение величин отрезков, лежащих на прямой, и их проекций сохраняется. Если точка В расположена на отрезке АС и делит его в определенном отношении, то её проекция В1 лежит на проекции А1С1 и делит ее в том же отношении.
5. Если прямые в пространстве параллельны друг другу, то параллельны и их одноименные проекции.
6. Если отрезок параллелен плоскости, то его проекция будет параллельна самому отрезку и равна его натуральной величине.
7. Плоская фигура проецируется на плоскость в натуральную величину, если она параллельна этой плоскости.
8. Прямой угол проецируется в натуральную величину, если одна его сторона параллельна, а вторая не перпендикулярна плоскости проекций.
Слайд 7 Виды проецирования
Процесс отображения точек пространственного предмета на плоскость проекций с
Виды проецирования Процесс отображения точек пространственного предмета на плоскость проекций с

Слайд 8ПРОЕКЦИИ ГЕОМЕТРИЧЕСКИХ ЭЛЕМЕНТОВ НА ОРТОГОНАЛЬНОМ ЧЕРТЕЖЕ
Метод параллельного проецирования является основным при составлении
ПРОЕКЦИИ ГЕОМЕТРИЧЕСКИХ ЭЛЕМЕНТОВ НА ОРТОГОНАЛЬНОМ ЧЕРТЕЖЕ
Метод параллельного проецирования является основным при составлении

Для получения проекций точки А на три
Плоскости проекций П1, П2 и П3 через точку А
Проводятся проецирующие лучи [AA1) – до
пересечения с плоскостью П1 , [AA2) – до
пересечения с плоскостью П2 и [AA3) – до
пересечения с плоскостью П3 .
Слайд 9 Для получения плоского чертежа точки А необходимо повернуть плоскость П1 вокруг оси
Для получения плоского чертежа точки А необходимо повернуть плоскость П1 вокруг оси

Плоский чертеж, получившийся после совмещения плоскостей проекций с плоскостью П2, принято называть эпюром (как минимум, 2 изображения предмета, связанных между собой линиями проекционной связи, расположенными перпендикулярно осям).
В зависимости от расположения точек относительно плоскостей проекций различают точки общего и частного положения (точки пространства, лежащие в плоскостях проекций).
Слайд 10ПРЯМАЯ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ
Способы задания прямой
Проекциями двух точек (конечным отрезком).
Точкой
ПРЯМАЯ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ
Способы задания прямой
Проекциями двух точек (конечным отрезком).
Точкой

Линией пересечения двух плоскостей.
Своими проекциями прямой.
Классификация прямых
В зависимости от положения прямых относительно плоскостей проекций различают прямые общего положения и прямые частного положения. Прямая общего положения – прямая, наклоненная под произвольными углами ко всем трем плоскостям проекций. Для решения задач в начертательной геометрии часто используются чертежи на двух совмещенных плоскостях проекций, которые называются двухкартинными комплексными чертежами.
Слайд 11 Принадлежность точки прямой линии. Точка принадлежит прямой, если ее проекции принадлежат соответствующим
Принадлежность точки прямой линии. Точка принадлежит прямой, если ее проекции принадлежат соответствующим

Следом прямой называется точка пересечения прямой с плоскостью проекций. Следы прямой являются точками частного положения, лежащими на плоскостях проекций. Поэтому горизонтальный след M совпадает со своей горизонтальной проекцией, а фронтальный след N – со своей фронтальной проекцией.
Слайд 12 Натуральная величина отрезка прямой равна гипотенузе прямоугольного треугольника, одним из катетов которого
Натуральная величина отрезка прямой равна гипотенузе прямоугольного треугольника, одним из катетов которого

Слайд 13Прямые частного положения
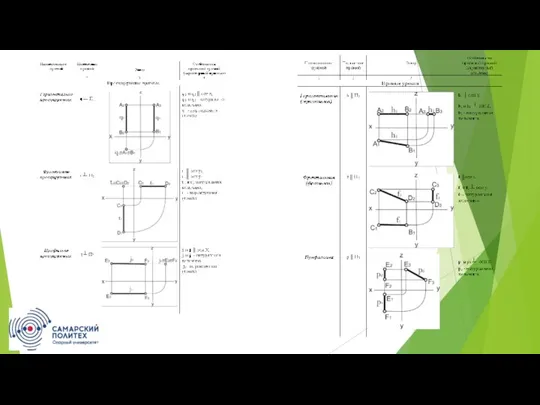
Среди прямых частного положения различают линии уровня и проецирующие прямые.
Прямые частного положения
Среди прямых частного положения различают линии уровня и проецирующие прямые.

Горизонтальяма параллельная горизонтальной плоскости проекций h || П1
Фронталь f – прямая, параллельная фронтальной плоскости проекций f || П2
Слайд 14Профильная прямая p – прямая, параллельная профильной плоскости проекций p || П3
Прямые
Профильная прямая p – прямая, параллельная профильной плоскости проекций p || П3
Прямые

Слайд 15 Прямая линия, перпендикулярная одной из плоскостей проекций или параллельная направлению проецирования, называется
Прямая линия, перпендикулярная одной из плоскостей проекций или параллельная направлению проецирования, называется

Горизонтально-проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций а ┴ П1.
Фронтально-проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций b ┴ П2
Слайд 16Профильно-проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций c┴ П3
Проецирующие прямые параллельны
Профильно-проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций c┴ П3
Проецирующие прямые параллельны

 Решения для бизнеса, основанные на открытом программном коде
Решения для бизнеса, основанные на открытом программном коде Штат Айова
Штат Айова Викторина «Золотое кольцо России»
Викторина «Золотое кольцо России» Стандартизация в России и других странах
Стандартизация в России и других странах Презентация на тему Физика твердого тела Кристаллофизика
Презентация на тему Физика твердого тела Кристаллофизика
 Технический анализ ценных бумаг
Технический анализ ценных бумаг Анализ диалогов из фильма Ирония судьбы
Анализ диалогов из фильма Ирония судьбы Природно-ресурсный потенциал России
Природно-ресурсный потенциал России Презентация на тему Древнегреческая цивилизация
Презентация на тему Древнегреческая цивилизация  Дыхательная гимнастика
Дыхательная гимнастика Проект Ботанический Сад
Проект Ботанический Сад Игры XXII Олимпиады
Игры XXII Олимпиады Лист. Строение листа
Лист. Строение листа Звездочёт
Звездочёт Договор транспортной экспедиции
Договор транспортной экспедиции АКСАКОВ КОНСТАНТИН СЕРГЕЕВИЧ (1817–1860)
АКСАКОВ КОНСТАНТИН СЕРГЕЕВИЧ (1817–1860) Организация труда персонала в ресторане высшего класса общегородского типа при подготовке банкета-коктейль-фуршет на 100 человек
Организация труда персонала в ресторане высшего класса общегородского типа при подготовке банкета-коктейль-фуршет на 100 человек Система «1С:Образование 4». Организация учебного процесса на основе цифровых образовательных ресурсов
Система «1С:Образование 4». Организация учебного процесса на основе цифровых образовательных ресурсов Практикум-18Воля и мотивация
Практикум-18Воля и мотивация Свойства параллелепипеда
Свойства параллелепипеда Развитие культуры письменной речи младших школьников на уроках русского языка
Развитие культуры письменной речи младших школьников на уроках русского языка Как сохранить значимые социально-политические особенности на фоне интернационализма
Как сохранить значимые социально-политические особенности на фоне интернационализма Raportul departamentului local de proiecte și constucții
Raportul departamentului local de proiecte și constucții Заполнение Психоматрицы. Занятие 2
Заполнение Психоматрицы. Занятие 2 Аэротренажер. Модернизация тренажера
Аэротренажер. Модернизация тренажера Рождественский турнир по хоккею с шайбой среди любительских команд
Рождественский турнир по хоккею с шайбой среди любительских команд Использование кавалетти для подготовки всадников в конкуре
Использование кавалетти для подготовки всадников в конкуре Семья Соколовых
Семья Соколовых