Ломакина Ирина Владимировна,учитель математики высшей квалификационной категории МОУ «Средняя общеобразовательная школа №11» г

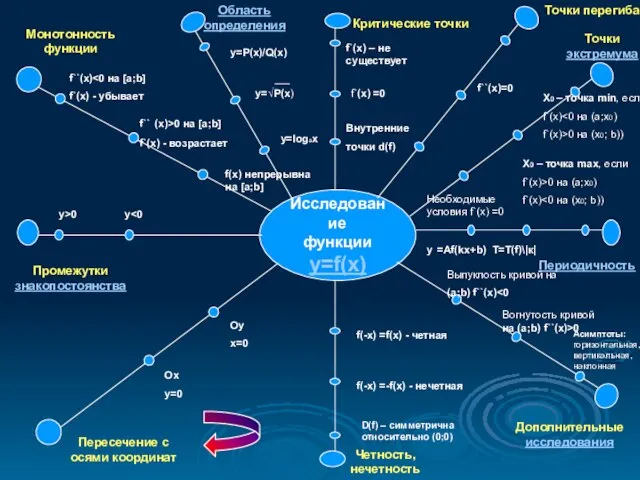
Исследование функции с помощью производной

Исследование
функции
y=f(x)

I. 1. Область определения
функции: х ≠ -3 и х ≠ 2
I. 2. Почему не существует график
функции?
Область определения функции
пустое множество.

II.1. Функция в нуль не обращается.
II.2. График функции ось абсцисс не пересекает.

III.1.Область определения функции симметрична относительно начала координат и выполняется равенство у(-х) = -у(х),значит функция нечетная.
III.2. у = (1-cos2x)/2, Т = 2π/2 = π

IV.1. Убывает на всей числовой оси функция у = -х³ - х, т.к. её производная
-3х² - 1 отрицательна при всех значениях х.
IV.2. Промежутки возрастания (-∞;-1,8], [0,2; ∞), убывания [-1,8;0,2], точка максимума х=-1,8, минимума х=0,2, точки перегиба нет.

V.1.Исследовать функцию
у = х³/6 + х²/2+1,7 на выпуклость,
вогнутость.
у΄= х ²/2 + х, у˝ = х +1,
у˝ = 0 при х =-1 – точка перегиба,
у˝ >0 при х>-1- функция выпукла вниз (вогнута);
у˝ <0 при х<-1- функция выпукла вверх.

Имеет ли функция точку перегиба на отрезке [1;2]
у΄= -4x³+12x²-8x, у˝ = -12x² + 24x – 8
у˝ = 0 -12x² + 24x – 8=0
3x² - 6x + 2=0
D = √3
x = 1 + √3/3, х = 1 - √3/3
1 + √3/3 – точка перегиба из отрезка [1;2]

ЭЙЛЕР (Euler) Леонард (1707-83), математик, механик, физик и астроном. По происхождению швейцарец. В 1726 был приглашен в Петербургскую АН и переехал в 1727 в Россию.

НЬЮТОН (Newton) Исаак (1643-1727), английский математик, механик, астроном и физик, создатель классической механики, Разработал дифференциальное и интегральное исчисления.
ЛЕЙБНИЦ (Leibniz) Готфрид Вильгельм (1646-1716), немецкий философ, математик, физик, языковед. Один из создателей дифференциального и интегрального исчислений.