Содержание
- 2. Цели урока: Повторить свойства квадратичной функции. Закрепить их знание при построении графиков квадратичной функции. Уметь определять
- 3. Учебно-воспитательные задачи: Образовательные: Приобретение знаний по применению графического изображения квадратичной функции. Применение приемов решения задач. Развивающие:
- 4. Оборудование: Геометрический инструмент. Компьютер Компьютерная презентация. Исторический материал. Метод: Словесный. Практический. Групповая работа. Защита проектов. Тип
- 5. Ход урока 1. Организационный момент. 2. Вести с урока. 1) повторить определение квадратичной функции, ее свойства
- 6. Определение. Функция вида у = ах2+bх+с, где а, b, c – заданные числа, а≠0, х –
- 7. График квадратичной функции -Парабола Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной
- 8. Свойства Парабола — кривая второго порядка. Она имеет ось симметрии, называемой осью параболы. Ось проходит через
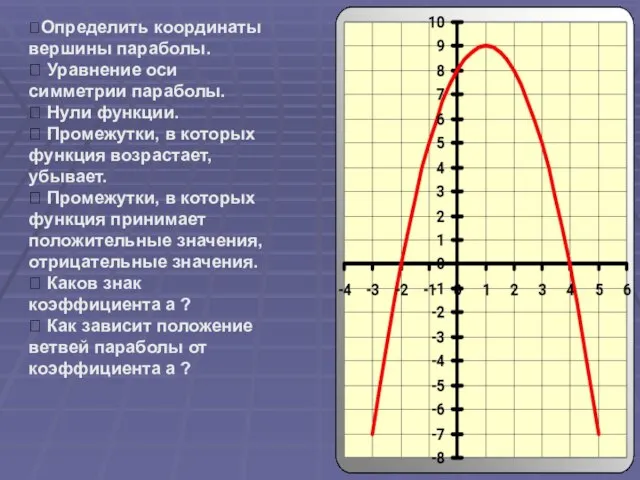
- 9. ⮚Определить координаты вершины параболы. ⮚ Уравнение оси симметрии параболы. ⮚ Нули функции. ⮚ Промежутки, в которых
- 10. Вершина параболы: Задание. Найти координаты вершины параболы: 1) у = х 2 -4х-5 2) у=-5х 2+3
- 11. Координаты точек пересечения параболы с осями координат. С Ох: у=0 ах2+bх+с=0 С Оу: х=0 у=с Задание.
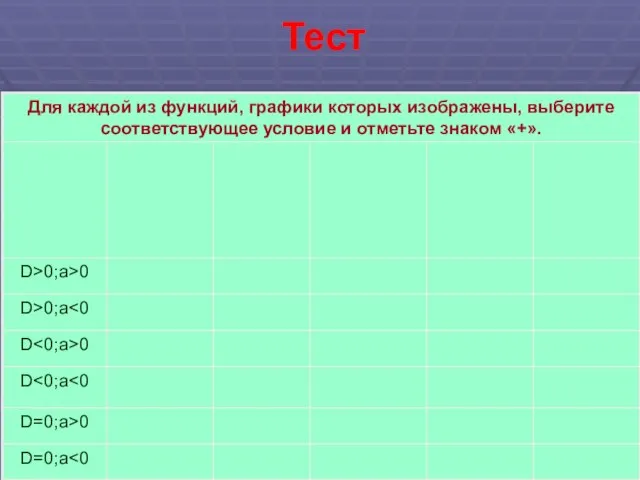
- 12. Тест
- 13. Построить график функции и по графику выяснить ее свойства. У = -х2-6х-8 Свойства функции: у>0 на
- 15. Скачать презентацию










 Группа «Минимизация рисков перехода на ФГОС НОО. Мониторинг ФГОС НОО»
Группа «Минимизация рисков перехода на ФГОС НОО. Мониторинг ФГОС НОО» Everyday slang. Сленг на каждый день
Everyday slang. Сленг на каждый день Степень сравнения прилагательных
Степень сравнения прилагательных Открытки с 9 мая
Открытки с 9 мая Понятие преступления и формы его множественности. Тема 3
Понятие преступления и формы его множественности. Тема 3 Разработка Учебных планов бакалавров и магистров по направлению «Энергетическое машиностроение» профиль подготовки бакалавров:
Разработка Учебных планов бакалавров и магистров по направлению «Энергетическое машиностроение» профиль подготовки бакалавров:  СТРУКТУРА РОССИЙСКОГО АВТОПАРКАГРУЗОВЫХ АВТОМОБИЛЕЙ ИАК «ВладВнешСервис», январь 2010
СТРУКТУРА РОССИЙСКОГО АВТОПАРКАГРУЗОВЫХ АВТОМОБИЛЕЙ ИАК «ВладВнешСервис», январь 2010 Прокачай в себе волонтера
Прокачай в себе волонтера praktika_po_zhkkh
praktika_po_zhkkh «Информационно-коммуникационные технологии в деятельности учителя математики»(18 часов)
«Информационно-коммуникационные технологии в деятельности учителя математики»(18 часов) Век медный,бронзовый, железный
Век медный,бронзовый, железный Литейное производство. Прибыли и холодильники отливок. (Лекция 7)
Литейное производство. Прибыли и холодильники отливок. (Лекция 7) Олимпида 2020
Олимпида 2020 Курительные смеси
Курительные смеси Holidays
Holidays Учимся мастерству
Учимся мастерству Муниципальное общеобразовательное учреждение«Средняя общеобразовательная школа № 13 »
Муниципальное общеобразовательное учреждение«Средняя общеобразовательная школа № 13 » Управление проектных продаж
Управление проектных продаж Арт-кластер Таврида
Арт-кластер Таврида Особенности предварительного расследования уголовных дел в отношении группы лиц с участием военнослужащих
Особенности предварительного расследования уголовных дел в отношении группы лиц с участием военнослужащих Рассмотрение дел о защите прав и законных интересов группы лиц. Лекция № 17
Рассмотрение дел о защите прав и законных интересов группы лиц. Лекция № 17 «Особенности преподавания русского языка по учебному комплексу Н.Г. Гольцовой, И.В. Шамшина»
«Особенности преподавания русского языка по учебному комплексу Н.Г. Гольцовой, И.В. Шамшина» Директор ФСИН России и его полномочия
Директор ФСИН России и его полномочия ЕВРАЗ: город друзей – город идей!
ЕВРАЗ: город друзей – город идей! НИ ДНЯ БЕЗ ПРАЗДНИКА!
НИ ДНЯ БЕЗ ПРАЗДНИКА! Презентация на тему Достопримечательности Бразилии
Презентация на тему Достопримечательности Бразилии  Как найти идею
Как найти идею Тургенев биография
Тургенев биография