Решение квадратичных неравенств

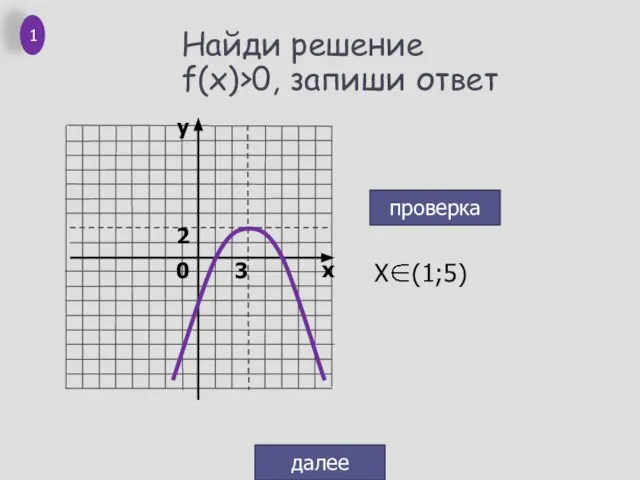
Найди решение
f(x)>0, запиши ответ
проверка
далее
1
0
2
3

f(x)<0
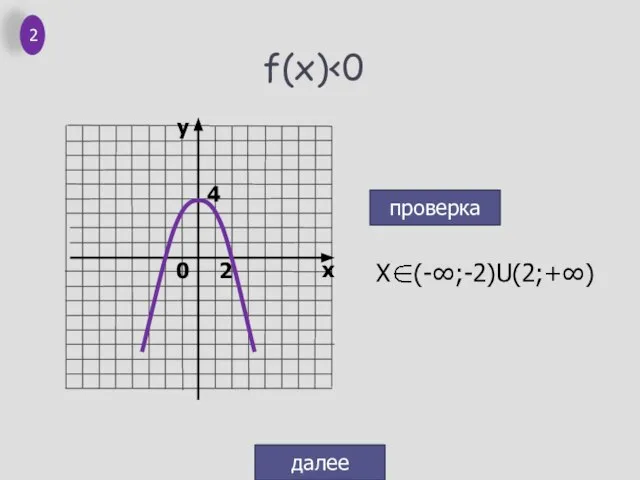
проверка
далее
2
0
4
2

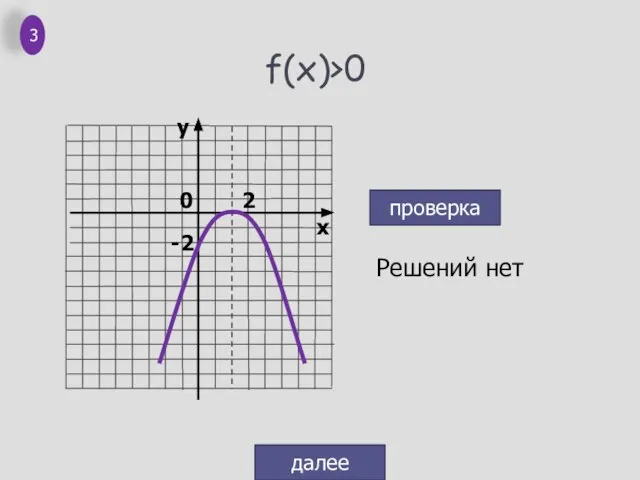
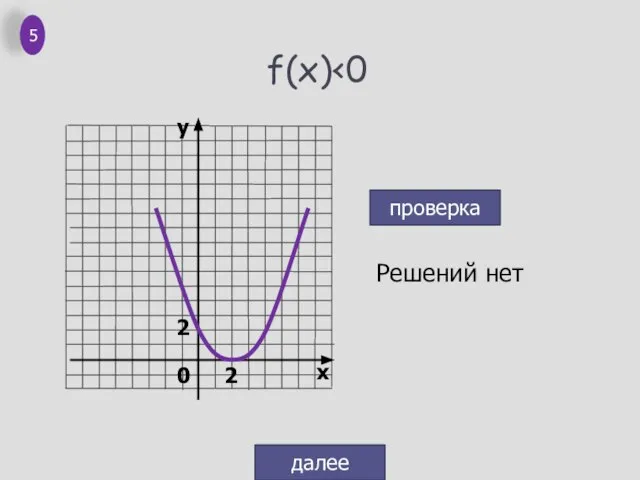
f(x)>0
Решений нет
проверка
далее
3
0
-2
2

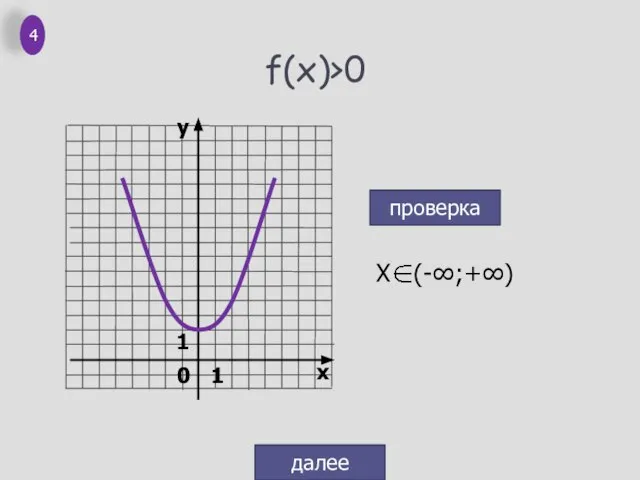
f(x)>0
проверка
далее
4
0
1
1

f(x)<0
Решений нет
проверка
далее
5
0
2
2

f(x)<0
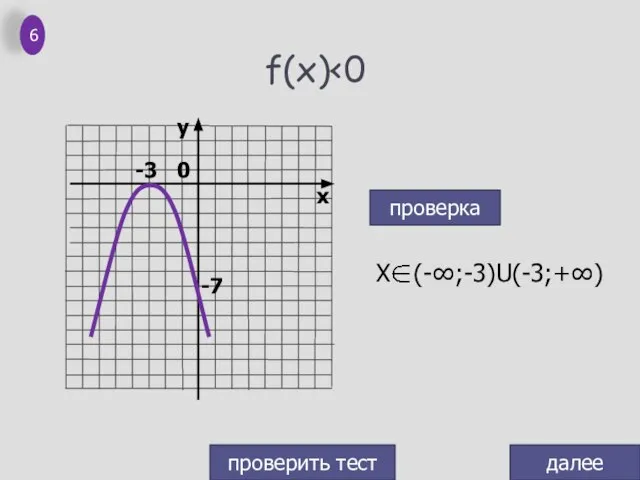
проверка
далее
проверить тест
6
0
-3
-7

Квадратичные неравенства
Неравенство вида
ах²+bх+с<0 (ах²+bх+с≤0, ах²+bх+с>0, ах²+bх+с≥0), где а, b, с-любые числа, а≠0, называется квадратичным.
Например: а) 2х²≥0
б) -4х²+8<0
в) 2х-х²≤0
г) 14х+5>3х²

5x²+9x-2 < 0
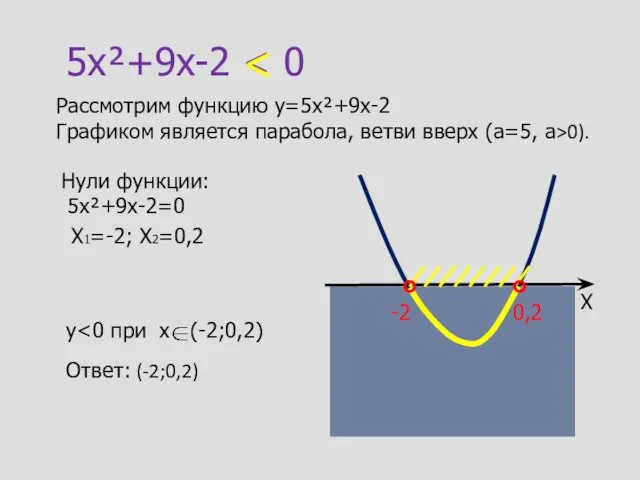
Рассмотрим функцию y=5x²+9x-2
Графиком является парабола, ветви вверх (а=5, а>0).
Нули функции: 5x²+9x-2=0
X1=-2; X2=0,2
X
-2
0,2
Ответ: (-2;0,2)
<

Чтобы решить квадратичное неравенство методом парабол, надо:
Рассмотреть функцию у=ах²+bх +с, определить направление ветвей;
Найти нули функции, решив квадратное уравнение ах²+bх+с=0;
Схематически построить параболу, учитывая направление ветвей и точки пересечения с осью х;
Учитывая знак неравенства, выбрать нужные промежутки и записать ответ.

3x²-11x-4 > 0
Рассмотрим функцию y=3x²-11x-4
Графиком является парабола, ветви вверх (а=3, а>0).
Нули функции: 3x²-11x-4=0
X1=-1/3; X2=4
X
-1/3
4
Ответ: (-∞; -1/3)U(4; +∞)
<

-1/4x²+2x-4<0
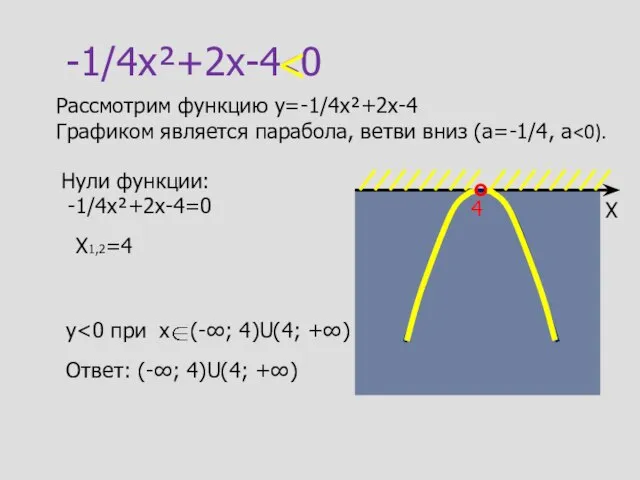
Рассмотрим функцию y=-1/4x²+2x-4
Графиком является парабола, ветви вниз (а=-1/4, а<0).
Нули функции:
-1/4x²+2x-4=0
X1,2=4
X
4
Ответ: (-∞; 4)U(4; +∞)
<

x²-3x+4 > 0
Рассмотрим функцию y=x²-3x+4
Графиком является парабола, ветви вверх (а=1, а>0).
Нули функции: x²-3x+4=0
D<0; действительных корней нет
X
Ответ: (-∞; +∞)
<
График функции с осью ox
не пересекается

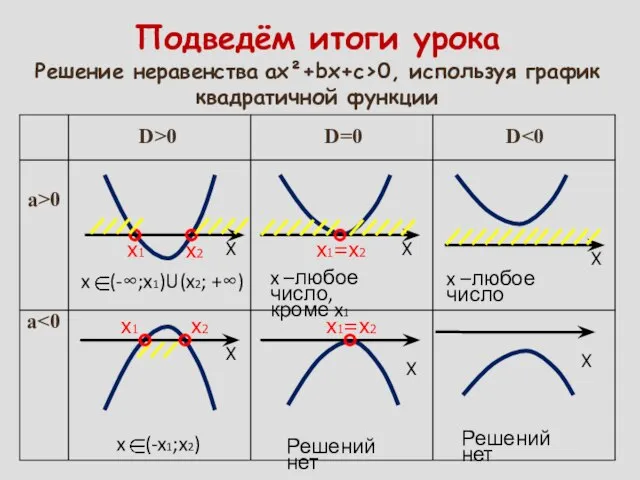
Подведём итоги урока
Решение неравенства ах²+bх+с>0, используя график квадратичной функции
X
x1
x2
D>0
D=0
D<0
a>0
a<0
X
x1=x2
x –любое число,
кроме x1
x –любое число
X
x1
x2
X
X
x1=x2
Решений нет
X
Решений нет