Содержание
- 2. Определение. Функция вида у = ах2+bх+с, где а, b, c – заданные числа, а≠0, х –
- 3. Графиком квадратичной функции является парабола, ветви которой направлены вверх(если а>0) или вниз (если а Например: у=2х²+4х-1
- 4. Чтобы построить график функции надо: Описать функцию: название функции, что является графиком функции, куда направлены ветви
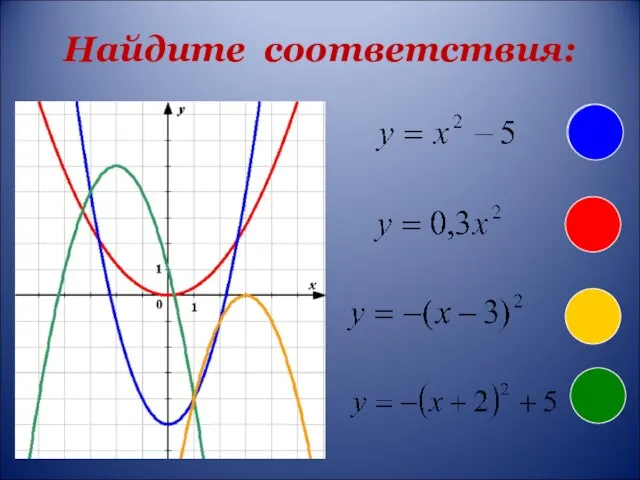
- 5. Найдите соответствия:
- 6. Вершина параболы: Задание. Найти координаты вершины параболы: 1) у = х 2 -4х-5 2) у=-5х 2+3
- 7. Координаты точек пересечения параболы с осями координат. С осью Ох: у=0 ах2+bх+с=0 С осью Оу: х=0
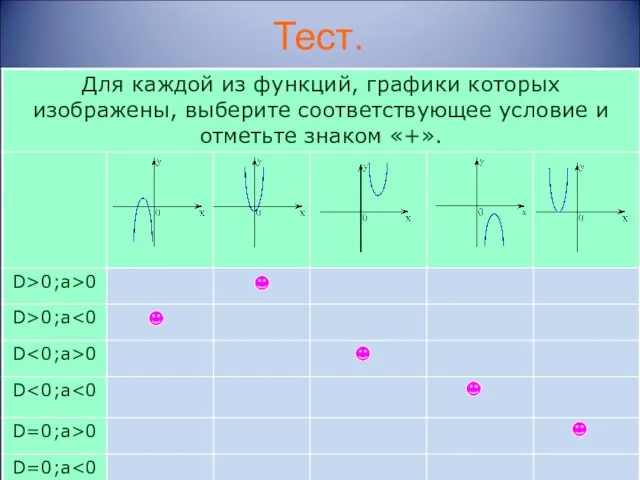
- 8. Тест.
- 9. Алгоритм построения графика функции у = ах2 + bх +с. 1. Определить направление ветвей параболы. 2.
- 10. Построить график функции и по графику выяснить ее свойства. y = -х2-6х-8
- 11. а Нули функции -4 и -2 Ось параболы х =-3 Таблица значений функции
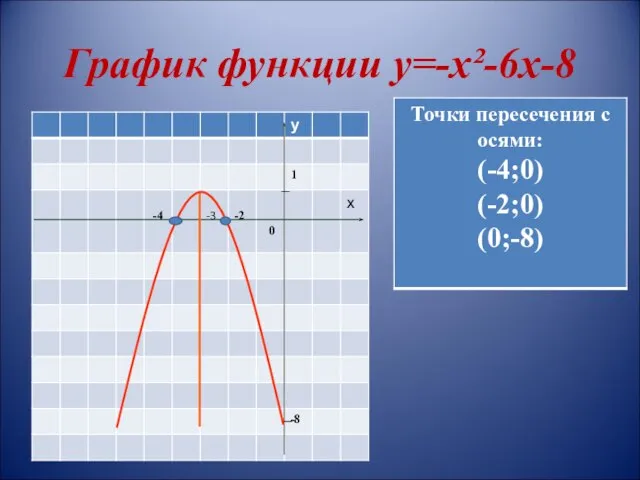
- 12. График функции у=-х²-6х-8
- 13. Свойства функции: у>0 на промежутке у Функция возрастает на промежутке Функция убывает на промежутке Наибольшее значение
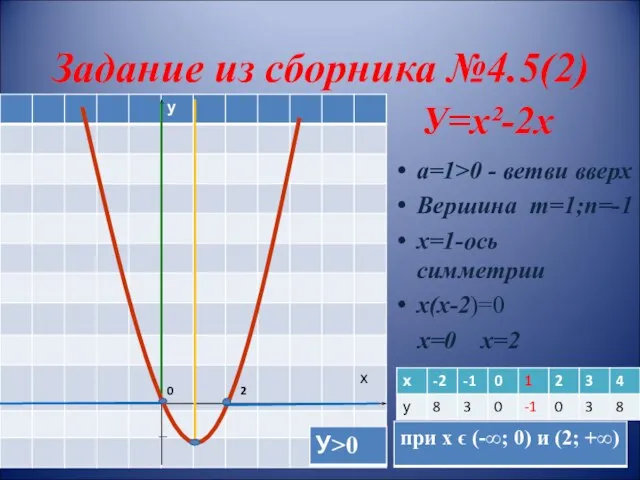
- 14. Задание из сборника №4.5(2) У=х²-2х а=1˃0 - ветви вверх Вершина m=1;n=-1 х=1-ось симметрии х(х-2)=0 х=0 х=2
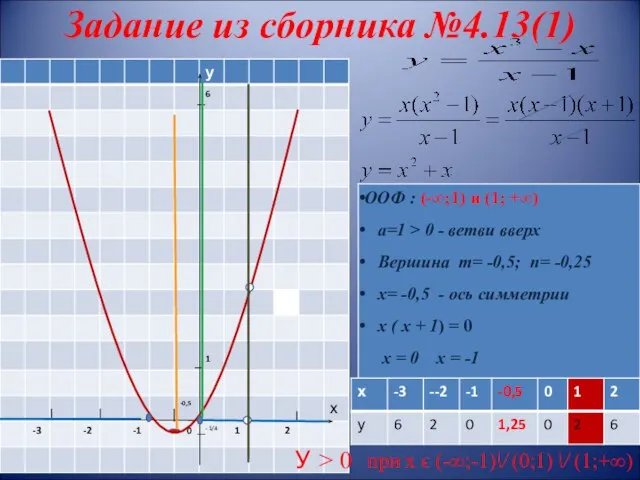
- 15. Задание из сборника №4.13(1) У ˃ 0 при х ϵ (-∞;-1) (0;1) (1;+∞)
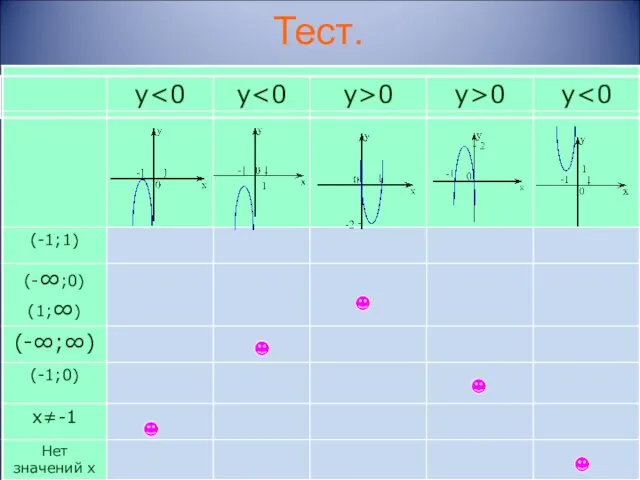
- 16. Тест.
- 17. Домашнее задание: № 4.17(2) №4.19 (2) № 4.9(2) № 4.8(2) № 4.13(2)
- 19. Скачать презентацию










 ORDERS OF ARCHITECTURE
ORDERS OF ARCHITECTURE Кабельные системы обогрева в строительстве
Кабельные системы обогрева в строительстве Презентация на тему Жаркие пустыни
Презентация на тему Жаркие пустыни Воронцов А.Б. 21 мая 2010
Воронцов А.Б. 21 мая 2010 Имидж, поведение и репутация как фактор жизненного успеха
Имидж, поведение и репутация как фактор жизненного успеха День матери
День матери Пингвины
Пингвины Политическая власть. Тема 3
Политическая власть. Тема 3 Разработка электрической винто-моторной группы для лёгкого летательного аппарата
Разработка электрической винто-моторной группы для лёгкого летательного аппарата  Детское воскресное служение
Детское воскресное служение Технология кислородной резки
Технология кислородной резки История вышивки лентами
История вышивки лентами 11 Программа развития МБСКОУ СКОШ 3 VIII вида г. Ишима на 2012 – 2014 гг. Департамент по социальным вопросам администрации г. Ишима Муницип
11 Программа развития МБСКОУ СКОШ 3 VIII вида г. Ишима на 2012 – 2014 гг. Департамент по социальным вопросам администрации г. Ишима Муницип Решение задач на движение
Решение задач на движение Olympiade in der Schule
Olympiade in der Schule Имущественные права личного характера в российском гражданском праве
Имущественные права личного характера в российском гражданском праве Ежегодно команда юношей принимает участиев межрегиональных соревнованиях среди кадетских корпусов, православных гимназий, дет
Ежегодно команда юношей принимает участиев межрегиональных соревнованиях среди кадетских корпусов, православных гимназий, дет Традиции Бурятии
Традиции Бурятии Сайт, который продает. Интернет магазин – это легко!
Сайт, который продает. Интернет магазин – это легко! Применение СУП в командной работе
Применение СУП в командной работе Н.В. Гоголь «Женитьба»
Н.В. Гоголь «Женитьба» Девиантное поведение
Девиантное поведение Педагогическая компетентность учителя как результат самообразования
Педагогическая компетентность учителя как результат самообразования Натюрморт с чучелом птицы
Натюрморт с чучелом птицы Право на оружие
Право на оружие "Ты не одинока"
"Ты не одинока" Курсы дистанционного обучения для электроэнергетики
Курсы дистанционного обучения для электроэнергетики Церковь Иль-Джезу
Церковь Иль-Джезу