Содержание
- 2. Квадратное уравнение Квадратным уравнением называется уравнение вида ах2 + bx + c = 0, где а,
- 3. Коэффициенты квадратного уравнения Числа а, b и с называют коэффициентами квадратного уравнения. ах2 + bx +
- 4. Неполное квадратное уравнение Квадратное уравнение, в котором хотя бы один из коэффициентов b или с равен
- 5. Виды неполных квадратных уравнений и их корни ах2 + c = 0, где с ≠ 0.
- 6. Виды неполных квадратных уравнений и их корни 2. ах2 + bx = 0, где b ≠
- 7. Виды неполных квадратных уравнений и их корни 3. ах2 = 0 Имеем единственный корень х =
- 8. Метод выделения полного квадрата Решить уравнение х2 + 14x + 24 = 0. Решение. х2 +
- 9. Формула корней квадратного уравнения Корни квадратного уравнения ах2 + bx + c = 0 можно найти
- 10. Формула корней квадратного уравнения Возможны 3 случая: 1. D > 0. Тогда уравнение имеет 2 различных
- 11. Формула корней квадратного уравнения 2. D = 0. Тогда уравнение имеет единственный корень: х2 - 4x
- 12. Формула корней квадратного уравнения 3. D Тогда уравнение не имеет корней, т. к. не существует .
- 13. Корни квадратного уравнения с четным вторым коэффициентом Если b = 2k, то корни уравнения ах2 +
- 14. Корни квадратного уравнения с четным вторым коэффициентом Решить уравнение 1. х2 + 18x + 32 =
- 15. Корни квадратного уравнения с четным вторым коэффициентом Решить уравнения 2. 3х2 + 2x + 1 =
- 16. Приведенное квадратное уравнение Приведенное квадратное уравнение – это уравнение вида х2 + px + q =
- 17. Формула корней приведенного квадратного уравнения х2 + px + q = 0. х2 - x -
- 18. Теорема Виета Теорема. Если х1 и х2 – корни приведенного квадратного уравнения х2 + px +
- 19. Теорема Виета для квадратного уравнения общего вида Теорема. Если х1 и х2 – корни квадратного уравнения
- 20. Теорема, обратная теореме Виета Теорема. Если числа х1, х2, р и q связаны условиями х1 +
- 21. Квадратный трехчлен Квадратным трехчленом называется многочлен вида а х2 + bx + c, где а, b,
- 22. Разложение квадратного трехчлена на линейные множители Теорема. Если х1 и х2 – корни квадратного трехчлена а
- 23. Неприводимый многочлен Если квадратный трехчлен ах2 + bx + c не имеет корней, то соответствующий многочлен
- 24. Уравнения, содержащие неизвестное в знаменателе Схема решения: Найти общий знаменатель дробей, входящих в уравнение. Умножить обе
- 25. Уравнения, содержащие неизвестное в знаменателе Общий знаменатель: (t + 1)(t - 2). Умножим на него обе
- 26. Уравнения, содержащие неизвестное в знаменателе Общий знаменатель: х(х – 3)(х + 3) . Тогда: 2х –
- 27. Биквадратные уравнения Уравнение вида ах4 + bx2 + c = 0, где а ≠ 0, b
- 28. Решение уравнений методом замены неизвестного Нет корней Ответ: 43.
- 29. Модуль Модуль числа х – это расстояние от начала отсчета до точки х на координатной прямой.
- 30. Уравнения, содержащие неизвестное под знаком модуля | х2 - 2х - 39| = 24. х2 -
- 31. Уравнения, содержащие неизвестное под знаком модуля 9х2 - = 0. x > 0, x 9х2 -
- 33. Скачать презентацию






























 Стандарт cXML в корпоративных приложениях электронной коммерции
Стандарт cXML в корпоративных приложениях электронной коммерции Целл-у-лосс - новинка от Herbalife. Деликатное выведение лишней жидкости из организма
Целл-у-лосс - новинка от Herbalife. Деликатное выведение лишней жидкости из организма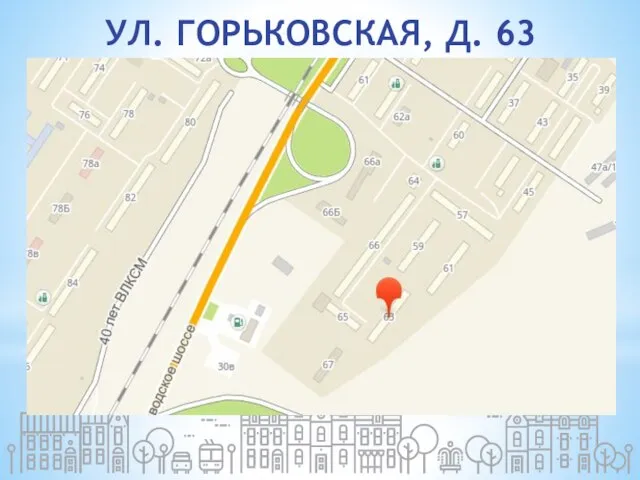 Улица Горьковская д. 63. Планируемые мероприятия
Улица Горьковская д. 63. Планируемые мероприятия Организация аварийно-спасательных работ
Организация аварийно-спасательных работ Знаток правил дорожного движения Знаток правил дорожного движения Юсупова Ирина Равиловна МОУ «СОШ 60», г. Набережные Челны.
Знаток правил дорожного движения Знаток правил дорожного движения Юсупова Ирина Равиловна МОУ «СОШ 60», г. Набережные Челны. Контроль якості металів і зварних з'єднань
Контроль якості металів і зварних з'єднань C новым учебным годом!!! 2012/13
C новым учебным годом!!! 2012/13 Презентация на тему Физика твердого тела Кристаллофизика
Презентация на тему Физика твердого тела Кристаллофизика
 посвящение в читатели
посвящение в читатели Строим домик из спичек
Строим домик из спичек Дню Защитника Отечества посвящается
Дню Защитника Отечества посвящается Изобразительность в музыке
Изобразительность в музыке SWOT-анализ
SWOT-анализ Народное прикладное искусство
Народное прикладное искусство Творчы праэкт Humanities Blues
Творчы праэкт Humanities Blues Рудольф Арнхейм
Рудольф Арнхейм Пэчворк
Пэчворк Особенности психологического сопровождения детей с ограниченными возможностями здоровья в условиях ДОУ
Особенности психологического сопровождения детей с ограниченными возможностями здоровья в условиях ДОУ Золотое сечение на Новгородчине
Золотое сечение на Новгородчине 家人
家人 Внешняя политика СССР в 1985-1991 гг
Внешняя политика СССР в 1985-1991 гг Жилищное право
Жилищное право Презентация на тему Социальная сфера презентация
Презентация на тему Социальная сфера презентация Экслибрис. Задание по прикладной композиции
Экслибрис. Задание по прикладной композиции Итоги интернет-урока«LEARNING MORE ABOUT LONDON / УЗНАЕМ БОЛЬШЕ О ЛОНДОНЕ»
Итоги интернет-урока«LEARNING MORE ABOUT LONDON / УЗНАЕМ БОЛЬШЕ О ЛОНДОНЕ» Хить Александр АнатольевичГенеральный директор ООО "Ассистанская компания"Украинская служба помощи" тел. 8 067 630 70 88 e-mail:
Хить Александр АнатольевичГенеральный директор ООО "Ассистанская компания"Украинская служба помощи" тел. 8 067 630 70 88 e-mail:  Олимпийское движение в России
Олимпийское движение в России Мышление. Тест Какой у вас тип мышления
Мышление. Тест Какой у вас тип мышления