КВАДРАТНЫЕ УРАВНЕНИЯ

Цель:
образовательные: углубить знания по теме «Квадратные уравнения»,вывести и доказать формулы корней квадратного уравнения, сформулировать умения применять формулы в решении задач;
развивающие: развивать умения в нахождении корней квадратного уравнения, абстрагировать и обобщать, развивать навыки самоконтроля;
воспитательные: воспитывать волю и настойчивость для решения поставленной задачи

1.Квадратные уравнения. Определение , примеры.
2.Неполные квадратные уравнения.
3.Метод выделения полного квадрата . Вывод формулы корней квадратных уравнений . Решение квадратных уравнений.
4.Приведённое квадратное уравнение.
5.Теорема Виета.
6.Теорема , обратная теореме Виета.
7.Разложение квадратного трёхчлена на множители.
8.Уравнения сводящиеся к квадратным.
9.Занимательные задачи.
10.Список используемого материала.

Квадратным уравнением называется уравнение
ax2+bx+c=0,
где a,b,c- заданные числа, a≠0.
x- неизвестное,
a- первый или старший коэффициент,
b- второй коэффициент,
с- свободный член.
Например:
х2+7x-24=0
4x2-x+5=0
2x2+6x=x2+3x+9
На главную
о!
Квадратное уравнение .
Далее

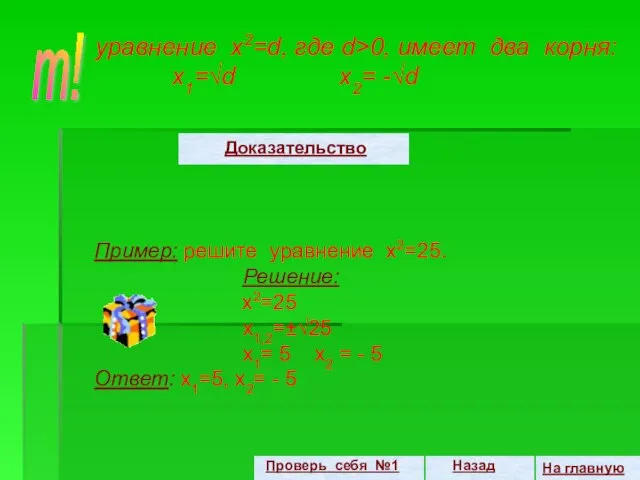
уравнение x2=d, где d>0, имеет два корня:
x1=√d x2= -√d
На главную
т!
Проверь себя №1
Пример: решите уравнение x2=25.
Решение:
x2=25
х1,2=±√25
x1= 5 x2 = - 5
Ответ: х1=5, х2= - 5

Неполные квадратные уравнения.
квадратное уравнение ax2+bx+c=0
называют неполным, если хотя бы один из
коэффициентов b или c равен 0.
ax2=0 , (b=c=0)
ax2+c=0 , (b=0) а≠0
ax2+b=0 , (c=0).
Например:
3х2=0 х2-6х=0
9х2-81=0 (х2-9)/(х-3)=0
На главную
о!

Метод выделения полного квадрата.
ax2+bx+c=0 , a ≠ 0 , /а На главную
=
-c
a
x2+
2bx
2a
+
=
х2+
+

!
Если b2-4ac≥0, то:
b2-4ac=D - дискриминант
- мы вывели формулу корней квадратного уравнения.

Пример: решите квадратное уравнение x2+2x-3=0
методом выделения полного квадрата.
Решение:
x2+2x-3=0
x2+2x=3 x2+2x+1=3+1
(x+1)2=4 , из этого следует :
x+1=2 , или x+1=-2 ,
x1=1 x2= - 3
Ответ: х1=1, х2= - 3
На главную

Формула квадратного уравнения .
если b2-4ac<0, то уравнение ax2+bx+c=0 не имеет действительных корней,
если b2-4ac>0, то уравнение ax2+bx+c=0 имеет два действительных корня,
если b2-4ac=0, то уравнение ax2+bx+c=0 имеет два равных корня (x1=x2)
!
На главную
Проверь себя №2

аx2+bx+c=0,если b-чётное число,
b=2m , a≠0 , m2-ac≥0
На главную
то Доказательство

x2+px+q=0 – приведённое квадратное уравнение ,
(ax2+bx+c=0, где a=1)
Любое квадратное уравнение аx2+bx+c=0 может быть приведённым , если разделить
обе части на а , а≠0
или
о!

Теорема Виета.
Если x1и x2 - корни уравнения x2+px+q=0,то справедливы формулы :
x1+x2=-p x1x2=q
т.е. сумма корней приведённого квадратного уравнения равна второму коэффициенту , взятому с противоположным знаком , а произведение корней равно свободному члену.
На главную
т!
Доказательство
Далее

Пример : один из корней уравнения x2-14x-15=0
положителен . Не решая уравнения , определить
знак второго корня.
Решение: По теореме Виета: x1x2= -15<0 , пусть x1>0 ( по
условию ),тогда x2<0.
Ответ : x2<0
На главную

Теорема , обратная теореме Виета.
т!
Если числа p , q ,х1, x2 – таковы, что x1+x2=-p , x1x2=q , то x1 и x2 - корни уравнения x2+px+q=0.
Доказательство:
х2+px+q=0
х1+x2=-p , x2x1=q
х2-x(x1+x2)+x1x2=x2-xx1-xx2+x1x2=x(x-x1)-x2(x-x1)=(x-x1)(x-x2),
т.е. х2+px+q=(x-x1)(x-x2)

Многочлен ax2+bx+c=0 , где а ≠ 0 , называют квадратным трёхчленом. Его можно разложить на множители способом группировки.
Теорема: если x1 и x2 - корни квадратного уравнения ax2+bx+c=0 , то при всех x справедливо равенство: ax2+bx+c=a(x-x1)(x-x2)
На главную
о!
Доказательство
Далее

аx2+bx+c=a(x-x1)2 , если D=0
аx2+bx+c=a(x-x1)(x-x2) , если D>0
Теорема: если квадратное уравнение ах2+bx+c=0
имеет корни х1 и х2 , то справедливо тождество
ax2+bx+c=а(х-х1)(х-х2). В случае , когда уравнение
имеет лишь один корень х1 , справедливо
тождество ax2+bx+c=a(x-x1)2 . Если уравнение не
имеет корней , то квадратный трёхчлен ax2+bx+с
не разлагается на множители .
На главную
т!
Проверь себя №4

Уравнения , сводящиеся к квадратным.
о!
Уравнение ax4+bx2+c=0 , где а≠0 , называют биквадратным. Решите биквадратное уравнение: 9х4+5х2-4=0. Решение: пусть х2=t , тогда x4=t2 , отсюда: 9t2+5t-4=0
D=25+4×4×9=169
t1=-1 , t2=8/18=4/9 x2= -1- не может быть x2=4/9 из этого следует x1,2=±2/3 Ответ: х1,2= ± 2/3
На главную

Решите уравнение: , О.Д.З.:х ≠-2 , х ≠3
Решение : , |× (х+2)(х-3), получим:
3(х-3)-4(х+2)=3(х+2)(х-3)
3х-9-4х-8=3х2+6х-9х-18
-х-17=3х2-3х-18
3х2+х+17-18-3х=0
3х2-2х-1=0
х1=1 х2=-1/3
Ответ: х1=-1/3 и х2=1
На главную

Решите уравнение: О.Д.З.:х≠1 и х≠2
Решение: умножим данное уравнение на (х-1)(х-2) 1+3(х-2)=(3-х)(х-1) 1+3х-6=3х-3-х2+х 1-6-х+х2+3=0 х2-х-2=0 х1,2=1/2±3/2 х1=2 х2=-1 х1=2-не подходит по О.Д.З.
Ответ : х=-1.
Корень х=2 - посторонний . При решении уравнения , содержащего неизвестное в знаменателе дроби , необходима проверка.
На главную

Решите уравнение:
Решение: х2+7х+12=0 х1,2=-7/2±1/2 х1=-4 и х2=-3 , х2+7х+12=(х+4)(х+3) , |×(х+4)(х+3) О.Д.З.:х≠-4 , х≠-3;получим:
(х+7)(х+3)-(х+4)+1=0 х2+7х+21+3х-х-4+1=0 х2+9х+18=0
х1,2=-9/2±3/2 х1 = -6 х2=-3 – не подходит по О.Д.З. Ответ: х = -6
На главную

На главную
1.Стая обезьян.
2.Ряд чисел.
3.Пчелиный рой.
4.Какие числа?
5.Интересное о дискриминанте.
6.Квадратное уравнение.
7.Теорема Виета.
Занимательные задачи.

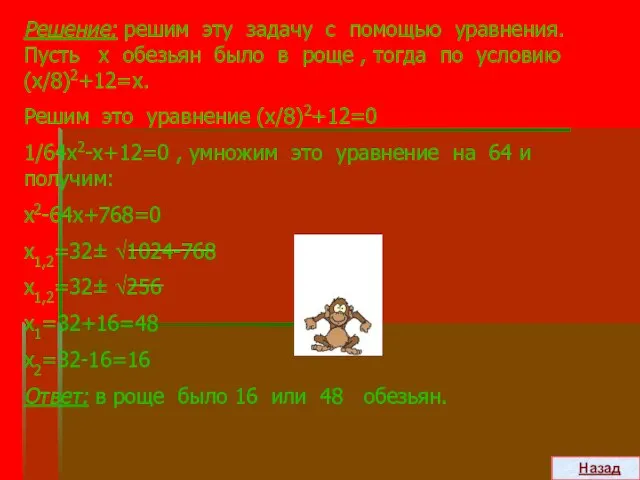
На две партии разбившись,
Забавлялись обезьяны.
Часть восьмая их в квадрате
В роще весело резвилась;
Криком радостным двенадцать
Воздух свежий оглашали.
Вместе сколько, ты мне скажешь ,
Обезьян там было в роще?
Решение
Стая обезьян.

Решение: решим эту задачу с помощью уравнения. Пусть х обезьян было в роще , тогда по условию (х/8)2+12=х.
Решим это уравнение (х/8)2+12=0
1/64х2-х+12=0 , умножим это уравнение на 64 и получим:
х2-64х+768=0
х1,2=32± √1024-768
х1,2=32± √256
х1=32+16=48
х2=32-16=16
Ответ: в роще было 16 или 48 обезьян.

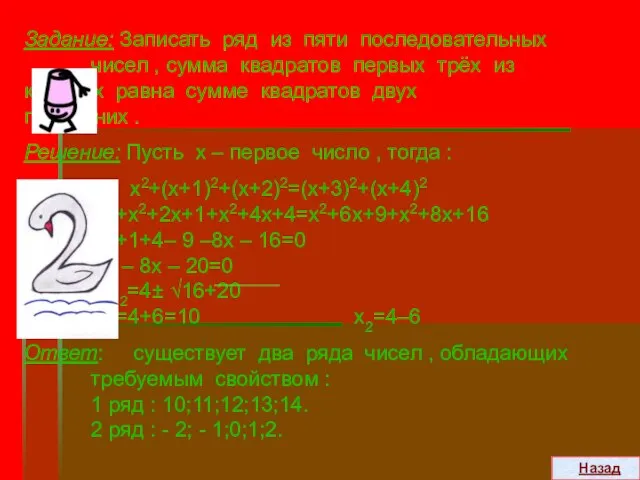
Задание: Записать ряд из пяти последовательных чисел , сумма квадратов первых трёх из которых равна сумме квадратов двух последних .
Решение: Пусть х – первое число , тогда :
х2+(х+1)2+(х+2)2=(х+3)2+(х+4)2 х2+х2+2х+1+х2+4х+4=х2+6х+9+х2+8х+16 х2+1+4– 9 –8х – 16=0 х2 – 8х – 20=0 х1,2=4± √16+20 х1=4+6=10 х2=4–6
Ответ: существует два ряда чисел , обладающих требуемым свойством : 1 ряд : 10;11;12;13;14. 2 ряд : - 2; - 1;0;1;2.

Пчёлы в числе , равном квадратному корню из
половины всего их роя , сели на куст жасмина ,
оставив позади себя 8/9 роя . И только одна пчёлка из
того же роя кружится возле лотоса , привлечённая
жужжанием подруги , неосторожно попавшей в западню
сладко пахнущего цветка . Сколько всего было пчёл в
рое?
Решение
Пчелиный рой.

Решение: Пусть всего пчёл было х , тогда : Решим это уравнение: √х/2=у , х=2у2 у+ +2=2у2 – |× 9; 9у+16у2+18-18у2=0 9у-2у2+18=0 – |× (-1) 2у2-9у-18=0 D=81+4×2×18=81+144=225 у1,2= у1=-6/4
у2=6
х1=2(-6/4)2=2(-3/2)2=2×9/4=4,5 , но число пчёл – натуральное, следовательно 4,5 – не подходит. х2=2×62=2×36=72
Ответ: всего было 72 пчёл в рое .

Задание: найти три последовательных числа , отличающихся
тем свойством , что квадрат среднего на 1 больше
произведения двух остальных .
Решение:
(х-1) и х и (х+1)
х2 - (х-1)(х+1)=1
х2-х2+1=1
Ответ : можно взять любы последовательные числа.
Какие числа?

Если вам скажут :“ Квадратное уравнение ,
дискриминант которого меньше нуля , не имеет
решения ” , можете уточнить : “ Не имеет решения в
действительных числах , в комплексных же имеет
целых два ”.
Пример:
х2–2х+5=0 х1,2=1± √ (1-5 ) х1,2=1± √ (- 4 ) х1=1+2i x2=1– 2i
Ответ: х1=1+2i
x2=1–2i

Задание: в уравнении 4х2–15х+4m2=0 , найти m так , чтобы один корень был квадратом другого .
Решение: х1=х22 (4m2)/4=х×х2 , значит m2=x3 , m=± √(x3)=±x √(x) .
х+х2=15/4 х =(15–4х2)/4 4х=15–4х2 4х2+4х–15=0 х1,2=(–2± √4+4×15 )/4 х1,2=(-2±8)/4 х1=-10/4 – не натуральное число под корнем . х2=6/4=3/2 m=±3/2 √(3/2)
Ответ: m=±3/2 √(3/2)

Задание: найти сумму квадратов корней уравнения
ax2+bx+c=0 , не находя его корней.
Решение:
x1+х2=- b/x
x1×x2 =c/a
x2+bx/a+c/a=0
x12+x22=(x1+x2)2-2x1x2=(-b/a)2-2c/a=b2/a2-2c/a=(b2-2ac)/a2
Ответ:х12+х22=(b2-2ас)/а2

Проверь себя №1.
1.Как будет выглядеть квадратное уравнение , если известны его коэффициенты а=2 , b=7 , с=-1 ? 1)2х2+7х+1=0+7х+1=0 2)2х2+7х – 1=0 +7х – 1=0 3)7х2+2х – 1 =0
2.Найдите корни уравнения х2=289 . Какой из них является арифметическим? 1)х=17 , это арифметический корень 2)х= -17 , это арифметический корень 3)х1=17, это арифметический корень ; х2=-17
3.Решите уравнение х2= – 16 1)х1,2=±4 2)х= –4 =±4 2)х= –4 3) нет действительных корней

Проверь себя №2.
1.Чему равен дискриминант уравнения 2х2+3х+1=0 1)D=9 2)+3х+1=0 1)D=9 2)D=17 +3х+1=0 1)D=9 2)D=17 3)D=1
2.Не решая уравнения 4х2– 7х –2=0 , скажите , сколько корней оно имеет ? 1)данное уравнение имеет один корень – 7х –2=0 , скажите , сколько корней оно имеет ? 1)данное уравнение имеет один корень 2)данное уравнение имеет два действительных корня 3)данное уравнение не имеет действительных корней
3.Продолжите фразу :» Если дискриминант меньше нуля , то …» 1)уравнение не имеет решения Если дискриминант меньше нуля , то …» 1)уравнение не имеет решения 2)уравнение не имеет действительных корней Если дискриминант меньше нуля , то …» 1)уравнение не имеет решения 2)уравнение не имеет действительных корней 3)уравнение имеет два равных корня

Проверь себя №3.
1.Один из корней уравнения х2 –15х +14=0 равен 1 .Чему равен второй корень ? 1) 14 –15х +14=0 равен 1 .Чему равен второй корень ? 1) 14 2) 15 –15х +14=0 равен 1 .Чему равен второй корень ? 1) 14 2) 15 3) –15
2.Не решая уравнения х2+2х – 80=0 , найдите сумму и произведение его корней . 1)х1+х2= – 80 ; х1х2 =2 =2 2)х1+х2= – 2 ; х1х2= – 80 80 3)х1+х2= 80 ; х1х2 =2
3.Как будет выглядеть приведённое квадратное уравнение , если известны его корни : х1=5 , х2=2 ? 1)х2–7х +10=0 –7х +10=0 2)х2+10х +7=0 3)х2–7х –10=0
Назад

Проверь себя №4.
1.Если 2х2+х-3=2(х-1)(х+3/2) ,то какие корни будет иметь уравнение 2х2+х-3=0 ? 1)х1=-1 ,х2=-3/2 2)=-3/2 2)х1=-1 ,х2=3/2 =3/2 3)х1=1 ,х2=-3/2 =-3/2 4)х1=1 ,х2=3/2
2.Разложите на множители квадратный трёхчлен х2- 15х+26 , если решением уравнения х2 - 15х+26 =0 являются корни х1=13 , х2=2 1)(х+13)(х+2) 2)(х-13)(х+2) 3)(х-13)(х-2) 3)(х-13)(х-2) 4)(х+13)(х-2)

ПРАВИЛЬНЫЙ ОТВЕТ
Проверь себя №1

ПРАВИЛЬНЫЙ ОТВЕТ
Проверь себя №2

ПРАВИЛЬНЫЙ ОТВЕТ
Проверь себя №3

ПРАВИЛЬНЫЙ ОТВЕТ
Проверь себя №4

НЕПРАВИЛЬНЫЙ ОТВЕТ
Проверь себя №1

НЕПРАВИЛЬНЫЙ ОТВЕТ
Проверь себя №2

НЕПРАВИЛЬНЫЙ ОТВЕТ
Проверь себя №3

НЕПРАВИЛЬНЫЙ ОТВЕТ
Проверь себя №4

Доказательство:
ax2+bx+c=0
ax2+2mx+c=0
D=4m2-4ac=4(m2-ac)

Доказательство:
х1= -p/2 + √ (p/2)2-q +
х2= -p/2 - √(p/2)2-q
х1+x2=-2p/2=-p , x1+x2=-p
х1x2=(-p/2)2=(√(p/2)2-q)2=(p/2)-(p/2)2+q2=q , x1x2=q

Доказательство:
Пр. часть a(x-x1)(x-x2)=ax2-axx2-axx1+ax1x2=ax2-а(х1+х2)х+ах1х2
х1 и x2 – корни уравнения ax2+bx+c=0, т.е.
уравнения x2+bx/a+c/а=0,то
по теореме Виета x1+x2=-b/а , x1x2=c/а
из этого следует: ax2-a(-b/a)x+ac/а=ах2+bx+c , что и
требовалось доказать.

Доказательство:
х2=d, d>0
х 2- d=0
d=(√d)2
x 2– (√d )2 =0 (x - √d)(x +√d)=0
x1=√d x2=-√d ,что и требовалось доказать.