Содержание
Слайд 2 Кв. уравнения в Древнем Вавилоне. Главное меню
Необходимость решать уравнения не только
Кв. уравнения в Древнем Вавилоне. Главное меню
Необходимость решать уравнения не только

первой, но и второй степени ёщё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей веры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводя только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилонии, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводя только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилонии, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Слайд 3 Кв. уравнения в Индии. Главное меню
Задачи на квадратные уравнения встречаются уже
Кв. уравнения в Индии. Главное меню
Задачи на квадратные уравнения встречаются уже

в 499 г.
В Древней Индии были распространены публичные соревнования в решении трудных задач.
В одной из старинных индийских книг говорится по поводу таких соревнований следующее: "Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи.
Задача знаменитого индийского математика Бхаскары:
Обезьянок резвых стая Всласть поевши, развлекаясь. Их в квадрате часть восьмая На поляне забавлялась. А 12 по лианам..... Стали прыгать, повисая. Сколько было обезьянок, Ты скажи мне, в этой стае?
В Древней Индии были распространены публичные соревнования в решении трудных задач.
В одной из старинных индийских книг говорится по поводу таких соревнований следующее: "Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи.
Задача знаменитого индийского математика Бхаскары:
Обезьянок резвых стая Всласть поевши, развлекаясь. Их в квадрате часть восьмая На поляне забавлялась. А 12 по лианам..... Стали прыгать, повисая. Сколько было обезьянок, Ты скажи мне, в этой стае?
 Компьютер и здоровье глаз
Компьютер и здоровье глаз Пейзаж.Времена года
Пейзаж.Времена года Организационное и информационное обеспечение фандрейзинга
Организационное и информационное обеспечение фандрейзинга Сложноподчиненное предложение. Повторение и обобщение изученного.
Сложноподчиненное предложение. Повторение и обобщение изученного. История радио и мобильной связи
История радио и мобильной связи А как ты знаешь физику?
А как ты знаешь физику? Презентация на тему Нефтяная промышленность
Презентация на тему Нефтяная промышленность  Изобразительное искусство барокко
Изобразительное искусство барокко Как начать бизнес в интернете?
Как начать бизнес в интернете? Sony Ericsson: Из VGA в HD
Sony Ericsson: Из VGA в HD Символика Краснодарского края
Символика Краснодарского края Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить.
Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить. Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020
Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020 Children's behavior and its influence on their future acts
Children's behavior and its influence on their future acts РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС
РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС Слова-паразиты, или экология речи
Слова-паразиты, или экология речи Иммунная система и канцерогенез
Иммунная система и канцерогенез  Подарки AI Journey. Предложения. Сберклауд
Подарки AI Journey. Предложения. Сберклауд Философские теории неврозов
Философские теории неврозов Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel)
Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel) Деструктивность учащегося и образовательной среды: точки соприкосновения
Деструктивность учащегося и образовательной среды: точки соприкосновения БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ
БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ Подготовка граждан к военной службе
Подготовка граждан к военной службе Ультразвуковые накладные расходомеры Flexim
Ультразвуковые накладные расходомеры Flexim Презентация для заказных проектов
Презентация для заказных проектов Поступление на государственную службу
Поступление на государственную службу Оценка достижений учащихся в разновозрастной группе
Оценка достижений учащихся в разновозрастной группе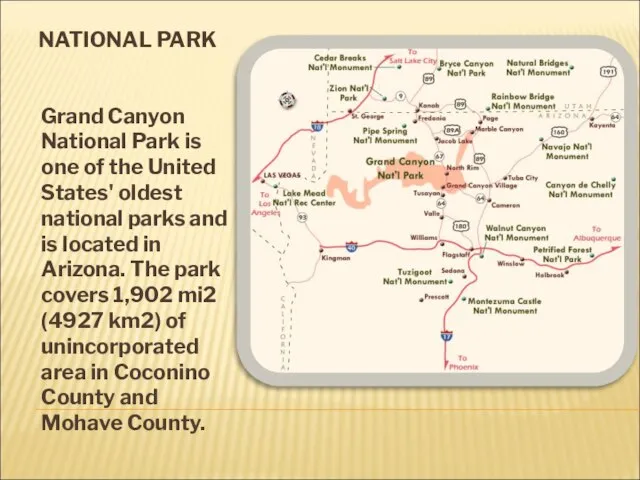 Grand Canyon National Park
Grand Canyon National Park