Содержание
- 2. Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной
- 3. Содержание Квадратный трехчлен Квадратичная функция Квадратные уравнения Разложение квадратного трёхчлена на множители
- 4. КВАДРАТНЫЙ ТРЕХЧЛЕН
- 5. Определение Многочлен ax²+bx+c , где а, в, с – числа (коэффициенты), причем а ≠ 0 называется
- 6. Назовите коэффициенты: 1) 2х² - 6х + 1 2) - 2х² + 8х – 5 3)
- 7. КВАДРАТИЧНАЯ ФУНКЦИЯ
- 8. Запомним Функция у = ax²+bx+c, где а, в, с – произвольные числа, причем а ≠0 называется
- 9. Ветви параболы у = ax²+bx+c направлены вверх, если а > 0, и вниз если а Как
- 10. Найти координаты вершины параболы, её ось симметрии и построить её: у = 2х² - 8х +
- 11. Самостоятельно: вычислить координаты вершины параболы 1) у = х² + 4х + 5 2) у =
- 12. Рефлексия: 1) Сегодня на уроке я запомнил… 2) Сегодня на уроке я научился… 3) Сегодня на
- 13. Квадратные уравнения
- 14. Содержание: Определение квадратного уравнения Классификация квадратных уравнений Способы решения квадратного уравнения
- 15. Определение Квадратным уравнением называется уравнение вида ax²+bx+c=0, где x - переменная, a, b, c – любые
- 16. Классификация . Квадратные уравнения. неполное полное b = 0; x² + c = 0 ах² +
- 17. Запомним Решить квадратное уравнение – это значит найти все его корни или установить, что их нет.
- 18. Способы решения квадратного уравнения: Разложением на множители Выделением полного квадрата По формуле корней (универсальный способ) По
- 19. Разложение левой части на множители
- 20. Например: Выделение полного квадрата
- 21. Рассмотрим ещё одно решение: Решим уравнение: х² + 6х - 7 = 0. Решение: х² +
- 22. Алгоритм решения квадратного уравнения ПО ФОРМУЛЕ КОРНЕЙ: Найти число, называемое дискриминантом квадратного уравнения и равное D
- 23. - если D=0, то данное квадратное уравнение имеет единственный корень, который равен - если D>0, то
- 24. Решить уравнение: 2x2- 5x + 2 = 0 Здесь a = 2, b = -5, c
- 25. Решить самостоятельно: x2- 2x + 1 = 0. 2x2- 3x +5= 0. Проверим 1 уравнение: получили
- 26. Работаем в парах: 1) Выберите квадратные уравнения и определите значения их коэффициентов: А) 2х² – 8
- 27. Проверим: Квадратные уравнения: А) 2х² – 8 = 0, где а=2; в=0; с=-8 Б) -х² +
- 28. Проверим: 2) Приведенные квадратные уравнения: И) х² + 5 - 2х = 0 3) Неполные квадратные
- 29. Пример решения квадратного уравнения Дано уравнение: Решение: Ответ:
- 30. Самостоятельная работа (по вариантам)
- 31. Проверь решение:
- 32. Проверь решение:
- 33. Запомни: по теореме Виета решаются только приведенные квадратные уравнения Теорема Виета: Если корни х₁ и х₂
- 34. НАПРИМЕР Дано приведённое квадратное уравнение x²-7x+10=0 Решение: методом подбора проверим числа 2 и 5. Их произведение
- 35. Решить : Решаем вместе: 1) х² - 15х + 14 = 0 2) х² + 3х
- 36. Проверим ответы: 1) х₁ =-1 х₂ =-7 2) х₁ = 1 х₂ = 18 3) х₁
- 37. Решение квадратных уравнений по коэффициентам Если сумма коэффициентов равна 0, т.е. а + в + с
- 38. Решить самостоятельно по группам: 1) 3х² + 4х + 1 = 0, 2) 5х² - 4х
- 39. Проверим:
- 40. Проверим:
- 41. Проверим:
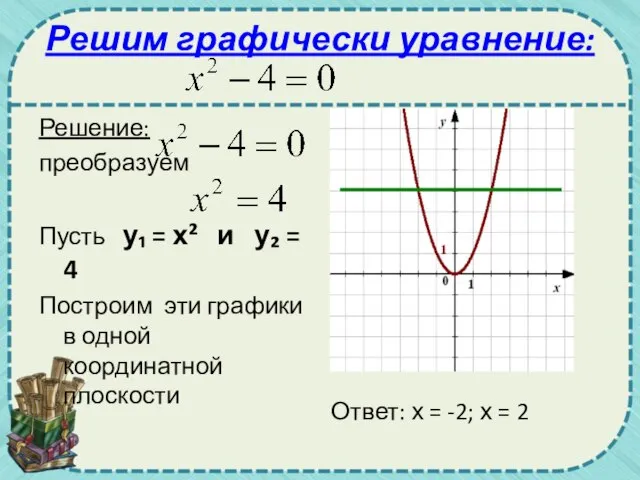
- 42. Решим графически уравнение: Решение: преобразуем Пусть у₁ = х² и у₂ = 4 Построим эти графики
- 43. Решить графически уравнения по вариантам: 1 вариант 1) х² + 2х – 3 = 0 2)
- 44. Введение новой переменной Умение удачно ввести новую переменную – облегчает решение Например: надо решить уравнение (2х+3)²
- 45. Решить самостоятельно в парах: а) (х² - х)² - 14(х² - х) + 24 = 0;
- 46. Разложение квадратного трехчлена на множители
- 47. Запомнить: Если квадратное уравнение ax²+bx+c=0 имеет корни х₁ и х₂, то квадратный трехчлен ax²+bx+c, раскладывается на
- 48. Разложите квадратный трехчлен на множители: 1 вариант 1) х² - 11х + 24 2) х² +
- 49. Проверим 1 вариант 1) (х-8)(х-3) 2) (х+3)(х+4) 3) – (х-1)(х+9) 4) 3·(х-1/6)(х+13/6) 5) -5·(х-1)(х- 0,2) 2
- 50. Рефлексия: Сегодня на уроке я запомнил… Сегодня на уроке я научился… Сегодня на уроке я узнал
- 51. СПАСИБО ЗА УРОК !!!
- 53. Скачать презентацию

















































 ВодорастворимыеРастительныеМасла (ВРМ)
ВодорастворимыеРастительныеМасла (ВРМ) Областные особенности русского костюма
Областные особенности русского костюма Проект на тему: Фэн-шуй ( | ) в классной комнате. - презентация
Проект на тему: Фэн-шуй ( | ) в классной комнате. - презентация Панели стеновые CPL
Панели стеновые CPL Подготовка к ЕГЭ. Решение задач на движение
Подготовка к ЕГЭ. Решение задач на движение Презентация замороженных фруктовых пюре и ягод Dira
Презентация замороженных фруктовых пюре и ягод Dira Зеленый наряд нашего города
Зеленый наряд нашего города Техника квиллинг
Техника квиллинг «Атлас флоры и фауны Белого моря» это коллективная монография, подготовленная большой группой специалистов. Книга дает возможнос
«Атлас флоры и фауны Белого моря» это коллективная монография, подготовленная большой группой специалистов. Книга дает возможнос Текхнология блокчейн: инвестиции в будущее
Текхнология блокчейн: инвестиции в будущее Выгода открытия бизнеса в 2020 году
Выгода открытия бизнеса в 2020 году Изменение фоновых картинок в презентациях PowerPoint и текстовом редакторе Word
Изменение фоновых картинок в презентациях PowerPoint и текстовом редакторе Word Романтизм в русской живописи XIX века
Романтизм в русской живописи XIX века Развитие методов синтеза, исследование физико-химических и электрофизических свойств модифицированных наноуглеродных и фторугл
Развитие методов синтеза, исследование физико-химических и электрофизических свойств модифицированных наноуглеродных и фторугл Профи-digest
Профи-digest lecture_5
lecture_5 Виды сказуемых
Виды сказуемых Radiographic Interpretation of Infections of Jaws
Radiographic Interpretation of Infections of Jaws phpm2fa0e_ovosibirskaya-oblast
phpm2fa0e_ovosibirskaya-oblast Итоги 2-й четверти
Итоги 2-й четверти Математика-царица наук?
Математика-царица наук? Экономический смысл налогообложения
Экономический смысл налогообложения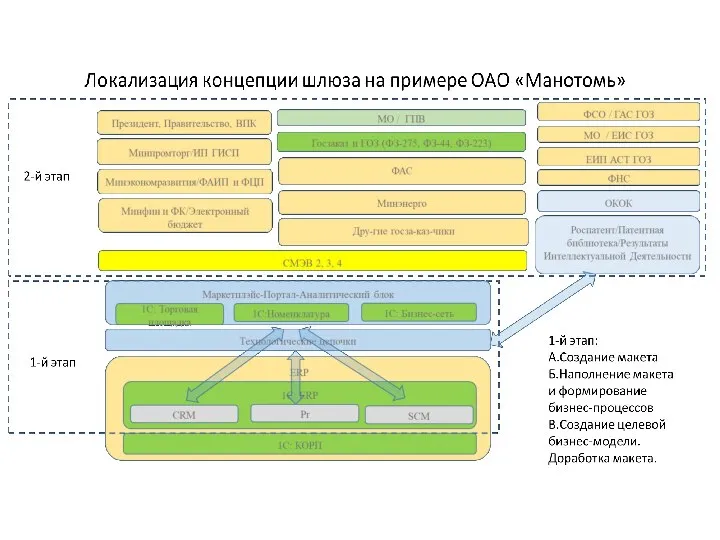 Локализация концепции шлюза на примере ОАО Манотомь
Локализация концепции шлюза на примере ОАО Манотомь Презентация на тему Справедливость и равенство
Презентация на тему Справедливость и равенство Protection of environment
Protection of environment Статусы пассажиров. Служебные пассажиры
Статусы пассажиров. Служебные пассажиры Буквы Ч и Щ в суффиксах имён существительных
Буквы Ч и Щ в суффиксах имён существительных Отдыхаем на отлично
Отдыхаем на отлично