Содержание
- 2. Выстроив дом лабиринтом с глухими стенами и крышей, Дедал – тогда замечательный гений в строительном деле
- 3. Содержание. Введение 1. Семью кругами к тайне 1.2. Большой каменный дом 1.3. Непреходящий символ 1.4. Как
- 4. Введение Лабиринт - архитектурное сооружение, сконструированное таким образом, что, однажды попав в него, невозможно или очень
- 5. Введение Лабиринт как символ Пути выражает идею движения человека к истине, это то, что вынуждает человека
- 6. Введение Другим названием лабиринта, широко распространенным в Западной Европе, было "троя". Вергилий упоминает об обрядовых играх,
- 7. 1. Семью кругами к тайне Первые похожие на лабиринт наскальные рисунки появились на Земле еще в
- 8. 1. Семью кругами к тайне Строго говоря, не всякий клубок запутанных ходов следует называть лабиринтом. Классический
- 9. 1. Семью кругами к тайне Иначе устроены ходы головоломки, именуемые на английский манер «мейзами» (maze). Мейзы
- 10. 1. Семью кругами к тайне Простейший лабиринт существовал во многих модификациях. автор легко увеличивал или уменьшал
- 11. 1.2. Большой каменный дом Таково буквальное значение греческого слова labyrinthos. Оно как нельзя лучше подходит Кносскому
- 12. 1.2. Большой каменный дом В 1900—1930 годах английский археолог Артур Эванс, проводя раскопки в Кносе, открыл
- 13. 1.2. Большой каменный дом Кносский дворец сильно пострадал во время извержения вулкана на острове Фера около
- 14. 1.2. Большой каменный дом Есть основания полагать, что в виде классического лабиринта возводили и крепостные стены
- 15. 1.3. Непреходящий символ Но лабиринты — это не только сооружения, гораздо чаще они встречаются как знаки,
- 16. 1.4. Как сразиться с Минотавром Лабиринт в христианской философии и архитектуре становится метафорой материального мира, проходя
- 17. 1.4. Как сразиться с Минотавром Многие из них были декорированы аллегорическими изображениями Тесея и Минотавра, сценами
- 18. 1.4. Как сразиться с Минотавром Искусство создания лабиринтов начало претерпевать значительные изменения с расширением представлений человека
- 19. Лабиринт, высаженный в 1670 году в саду виллы Альтьери в Риме, стал излюбленной забавой Папы Климента
- 20. 1.5. Дорога без конца Главной неразгаданной загадкой древнего символа остается его происхождение. Так и не смогли
- 21. 1.5. Дорога без конца На роль его «прародителей» претендуют и наскальные изображения концентрических колец в виде
- 22. 1.5. Дорога без конца История лабиринта по-прежнему не закончена. Его дороги, словно бесконечная лента времени, стремятся
- 23. Суеверия из лабиринта В древности изображение лабиринта считали прекрасным оберегом. Так, индейские племена тохоно и пима
- 24. Суеверия из лабиринта - Отправляясь в опасное место, можно попробовать нарисовать узор лабиринта на ладони. И
- 25. Суеверия из лабиринта Нет на земле более загадочных построек, чем лабиринты. Они манят, запутывают, пугают и
- 26. 2. Геометрическая постановка задачи о лабиринтах. Аллеи, дорожки, коридоры, галереи лабиринта тянутся, изгибаясь во все стороны,
- 27. 2. Геометрическая постановка задачи о лабиринтах. Эйлер установил четыре основных правила, которые применимы к сетям. Число
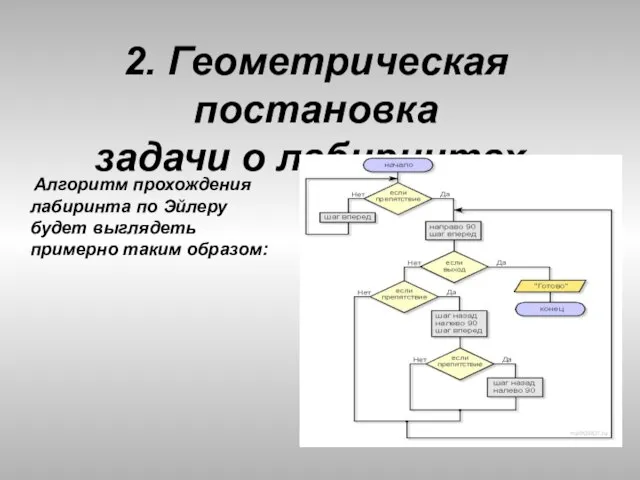
- 28. 2. Геометрическая постановка задачи о лабиринтах. Алгоритм прохождения лабиринта по Эйлеру будет выглядеть примерно таким образом:
- 29. 3. Решение задачи. Правило 1. Отправляемся по дороге от начального пункта (первого перекрестка) и идем по
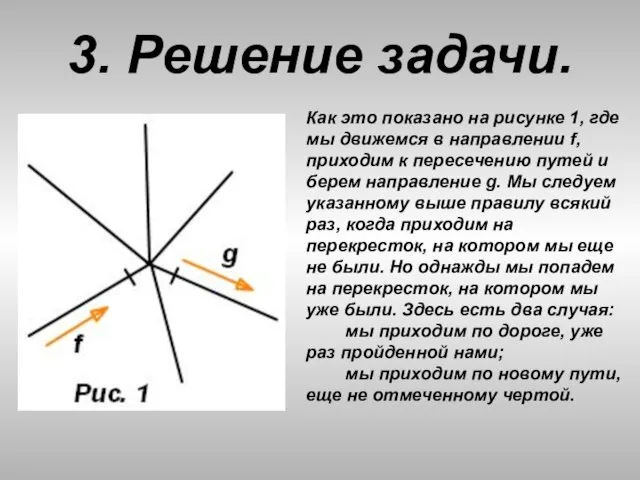
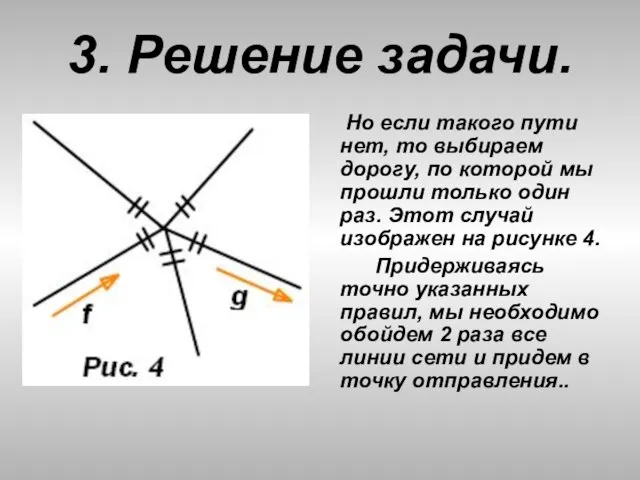
- 30. 3. Решение задачи. Как это показано на рисунке 1, где мы движемся в направлении f, приходим
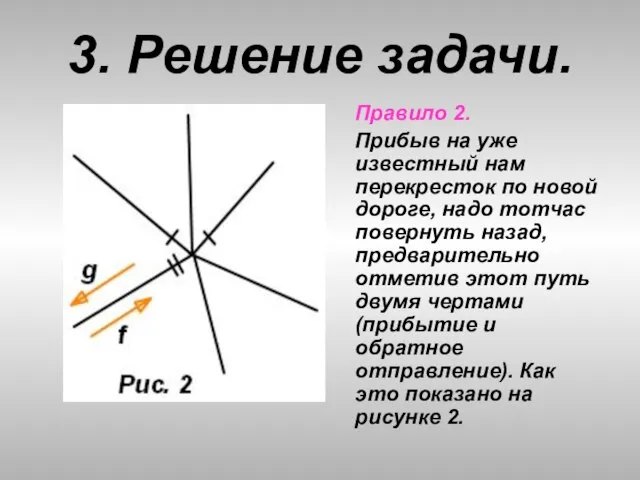
- 31. 3. Решение задачи. Правило 2. Прибыв на уже известный нам перекресток по новой дороге, надо тотчас
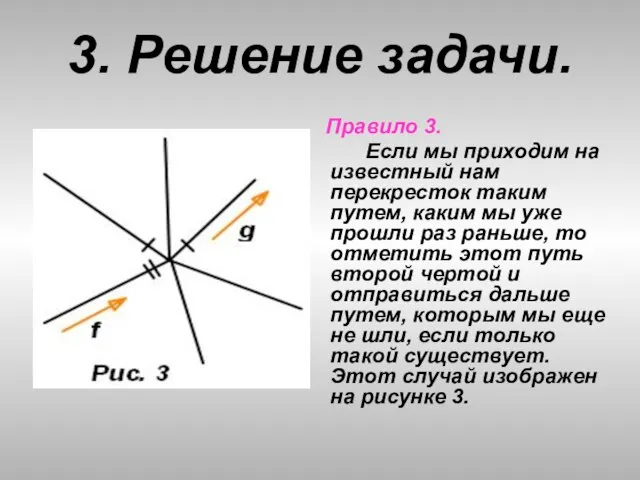
- 32. 3. Решение задачи. Правило 3. Если мы приходим на известный нам перекресток таким путем, каким мы
- 33. 3. Решение задачи. Но если такого пути нет, то выбираем дорогу, по которой мы прошли только
- 34. 3. Решение задачи. Итак, можно пройти каждую линию лабиринта дважды и прийти в исходную точку, если:
- 35. 3. Решение задачи. Пусть, наконец, мы будем вынуждены закончить путь и возвратиться в пункт А. Назовем
- 36. 3. Решение задачи. Итак, при последнем возвращении в А все пути в Z должны быть отмечены
- 37. 3. Решение задачи. Исследование сетей, называемое сейчас теорией графов, имеет широкое приложение в математике, электротехнике, вычислительной
- 39. Скачать презентацию































 Стипендия Правительства области
Стипендия Правительства области المالية االستدامة المالية
المالية االستدامة المالية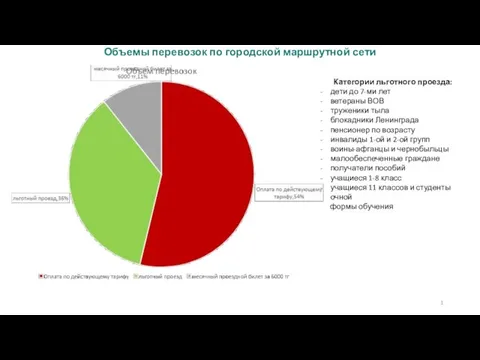 Объемы перевозок по городской маршрутной сети
Объемы перевозок по городской маршрутной сети День инвалида
День инвалида Презентация на тему Интернет и его возможности
Презентация на тему Интернет и его возможности Extenzionálne modely. Algebraická teória. Transformácie intervalov. Definícia funkcie Glob. (Téma 5)
Extenzionálne modely. Algebraická teória. Transformácie intervalov. Definícia funkcie Glob. (Téma 5) Культура Древней Греции
Культура Древней Греции Штриховая гладь
Штриховая гладь Профессия Повар-кондитер
Профессия Повар-кондитер Организационное стимулирование. Условия для внедрения мотивации персонала
Организационное стимулирование. Условия для внедрения мотивации персонала Что такое бенилюкс?
Что такое бенилюкс? Презентация на тему Здоровьесберегающие технологии на уроках в начальной школе. Окружающий мир 3 класс
Презентация на тему Здоровьесберегающие технологии на уроках в начальной школе. Окружающий мир 3 класс  FOOD SAFETY
FOOD SAFETY  Ассирия
Ассирия Презентация на тему Кометы и метеоры
Презентация на тему Кометы и метеоры Руководство Ernst&Young по составления бизнес-планов
Руководство Ernst&Young по составления бизнес-планов Куклы из махровых носков
Куклы из махровых носков Конституционные суды Приволжского Федерального округа
Конституционные суды Приволжского Федерального округа Японская каллиграфия - диалог культур Токио - Красноярск
Японская каллиграфия - диалог культур Токио - Красноярск «Пилот»: Маркетинг в компании
«Пилот»: Маркетинг в компании Устный журнал. В мире имён и названий
Устный журнал. В мире имён и названий Баскетбол. Тест по физической культуре
Баскетбол. Тест по физической культуре Материаловедение 5-6р
Материаловедение 5-6р Применение приборов серии IVS для решения задач вибродиагностики
Применение приборов серии IVS для решения задач вибродиагностики Композиционное решение для предприятий автомобилестроительной отрасли на основе системы MFG/PRO
Композиционное решение для предприятий автомобилестроительной отрасли на основе системы MFG/PRO Никола Тесла-повелитель молний
Никола Тесла-повелитель молний Проверка понимания озвученного текста
Проверка понимания озвученного текста Представление графической информации в компьютере
Представление графической информации в компьютере