Содержание
- 2. - плотность частиц - средняя скорость - хаотическая скорость - температура -давление
- 3. Если столкновения в плазме отсутствуют При наличии столкновений При упругих столкновениях
- 4. Если на частицу плазмы не действуют силы неэлектрической природы Масштаб усреднения В состоянии термодинамического равновесия Если
- 5. - приближение для интеграла столкновений При рассмотрении токов в полностью ионизованной плазме Интеграл столкновений в форме
- 6. Если , то (уравнение Власова) Если , то следует учитывать многочастичные корреляции . Если - магнитогидродинамическое
- 7. Дрейфовое кинетическое уравнение (критерий замагниченности) - функции распределения центров ларморовских кружков в пятимерном фазовом пространстве
- 8. Уравнения переноса × т.к Уравнение непрерывности ρ=mn ρe=en
- 9. Уравнение движения
- 10. При изотропии хаотических скоростей π=0. В случае упругих столкновений, т.к. τ - приближение
- 11. Уравнение переноса энергии × - плотность потока тепла - выделение тепла за счет столкновений с остальными
- 12. В случае упругих соударений Уравнение баланса тепла Уравнение для температуры
- 13. Энтропия, приходящаяся на одну частицу Связь πij, q, R, Q с n, V, Т можно найти
- 14. Двухжидкостная магнитная гидродинамика
- 15. где Током смещения можно пренебречь, если B/L>>E/ct или B>>VE/c . E/L~B/ct т.е. ~VB/c. Током смещения можно
- 16. Одножидкостная магнитная гидродинамика плотность массы гидродинамическая скорость Не вошло
- 17. Уравнение движения в одножидкостном пределе
- 18. - полное давление В F входят вязкость, электрические силы (и могут входить другие силы не электрической
- 19. Тензор максвелловских натяжений - вектор Умова-Пойнтинга В приближении одножидкостной магнитной гидродинамики рассматриваются большие масштабы и малые
- 20. Условия, при которых можно пользоваться (1) (2) E~VB/с если
- 21. Уравнение переноса энергии При, вязкость ионов всегда гораздо больше, чем электронов, поэтому вязкость плазмы целиком определяется
- 22. Уравнение баланса тепла
- 24. Скачать презентацию
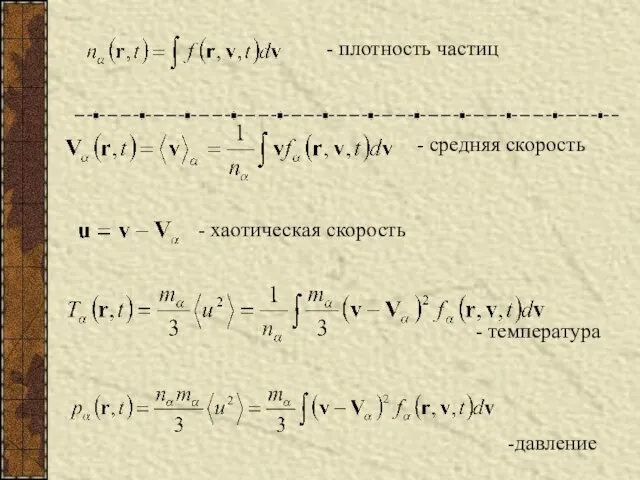







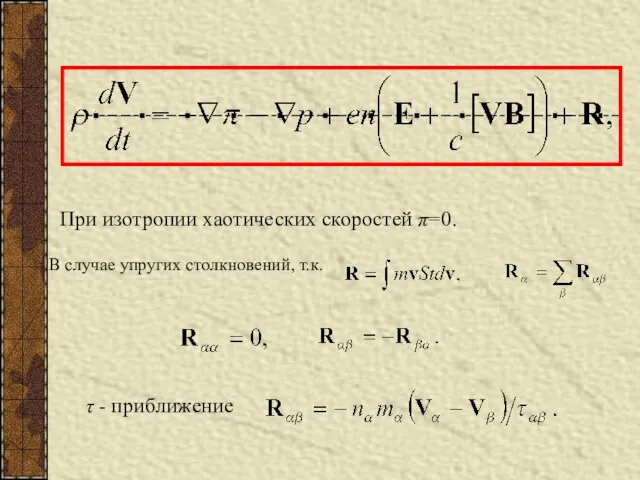







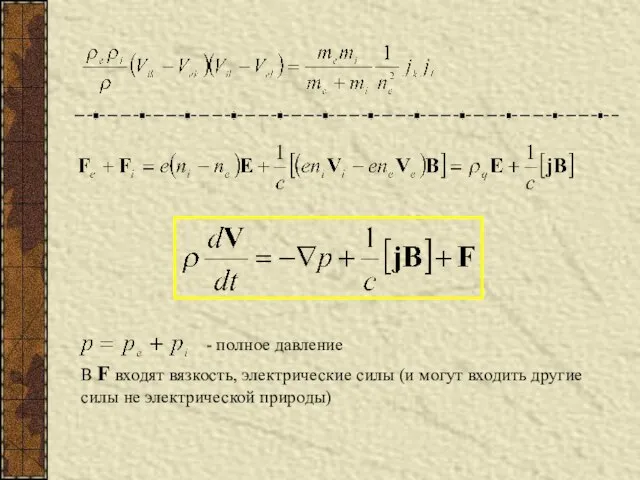

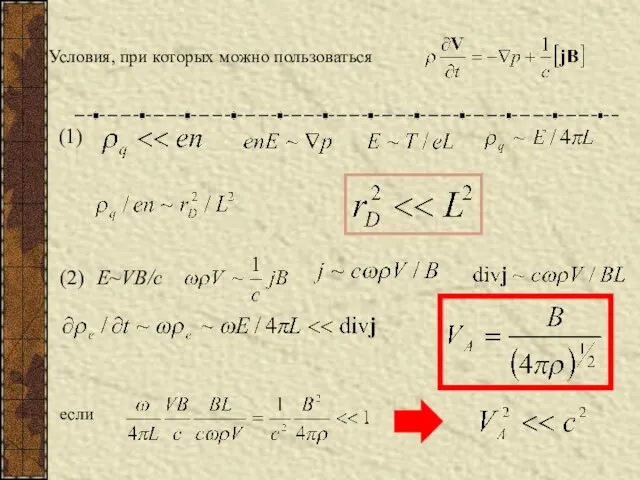


 Презентация на тему Презентация Венгрия
Презентация на тему Презентация Венгрия Материалы к круглому столу на тему:«О возможных схемах и механизмах финансирования управляющих компаний (организаций), профессио
Материалы к круглому столу на тему:«О возможных схемах и механизмах финансирования управляющих компаний (организаций), профессио Описание пищевой (легкой) промышленности России
Описание пищевой (легкой) промышленности России Законы арифметических действий
Законы арифметических действий Анализ особенностей трансляционных рисков в промышленности
Анализ особенностей трансляционных рисков в промышленности Проблема бытия в философии Нового времени
Проблема бытия в философии Нового времени Презентация Нутрициология
Презентация Нутрициология Барокко как стиль в искусстве
Барокко как стиль в искусстве Приемы видеомонтажа. Восьмерка
Приемы видеомонтажа. Восьмерка Водоросли
Водоросли Сталинград перед войной Сталинградская битва 23 августа 1942 года – 2 февраля 1943 года.
Сталинград перед войной Сталинградская битва 23 августа 1942 года – 2 февраля 1943 года. Обзор продукции Valtec
Обзор продукции Valtec Презентация по географии на тему:«Санкт-Петербург»
Презентация по географии на тему:«Санкт-Петербург»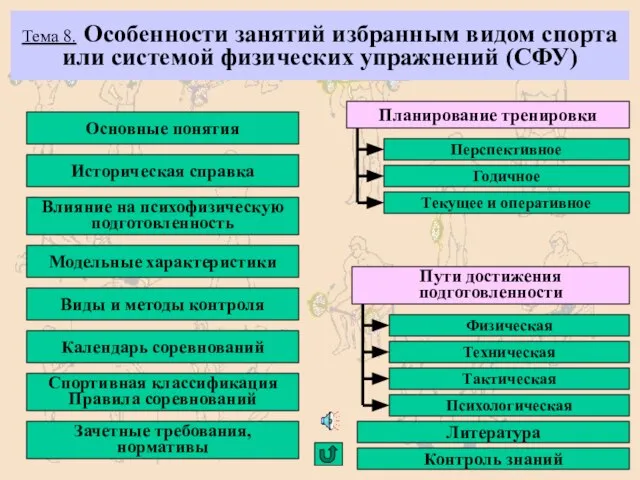 Особенности занятий избранным видом спорта
Особенности занятий избранным видом спорта «Основам информационных технологий»
«Основам информационных технологий» икона Николая Чудотворца
икона Николая Чудотворца История о том как Землю изгнали из центра Вселенной
История о том как Землю изгнали из центра Вселенной Old PostcardsСтарые почтовые открытки Музыка
Old PostcardsСтарые почтовые открытки Музыка Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах
Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах Дипломная работа. Виды диспетчерской документации, этапы обработки, документооборот диспетчера на автотранспортного предприятия
Дипломная работа. Виды диспетчерской документации, этапы обработки, документооборот диспетчера на автотранспортного предприятия «Система мониторинга освоения детьми планируемых результатов освоения Программы».
«Система мониторинга освоения детьми планируемых результатов освоения Программы». Об итогах социально – экономического развития Никифоровского сельского поселения Чусовского муниципального района Пермского кр
Об итогах социально – экономического развития Никифоровского сельского поселения Чусовского муниципального района Пермского кр Презентация на тему Паразиты человека
Презентация на тему Паразиты человека  Маска для искусственного сна
Маска для искусственного сна Работа с концептами как одна из форм реализации лингвокультурологического подхода
Работа с концептами как одна из форм реализации лингвокультурологического подхода Инкотермс 2010 Подготовили Столбова А.А.Т-086 Тихомирова Л.В.Т-083
Инкотермс 2010 Подготовили Столбова А.А.Т-086 Тихомирова Л.В.Т-083 Презентация на тему Динамика Масса и импульс тела Силы
Презентация на тему Динамика Масса и импульс тела Силы
 Урок по повести Н. В. Гоголя «Портрет»
Урок по повести Н. В. Гоголя «Портрет»