Лекция 4Раздел 2Случайные величины (числа) (Основы теории распределений вероятностей)

2.1 Понятие и виды случайных величин
В алгебре событий для описания ВЭ было аксиоматически
введено понятие вероятностного пространства: (Ω,A,P).
В терминах содержательно приближенных к описанию окружающего
мира оно позволяет исследовать вероятностные закономерности:
математически описывать ВЭ,
вычислять вероятности случайных событий и т.д.
Неприспособленность теоретико-множественных моделей для
применения средств математического анализа существенно
ограничивает использование категорий событий для
исследования ВЭ.
Значительные возможности появляются при переходе к числовой интерпретации случайных событий. Это позволяет описывать ВЭ как свойства соответствующих чисел привычным образом. Данный подход типичен для математики, когда содержательные понятия заменяют на числовые или функциональные аналоги. Так будем поступать для дальнейшего изучения ТВ.

Случайная величина
Определение. Случайной величиной (СВ) на вероятностном пространстве (Ω,A,P) называют измеримую (числовую) скалярную функцию ξ = ξ(ω), определенную на элементах Ω и принимающую действительные значения из R(1) = (- ∞, + ∞).
Для обозначения СВ принято использовать строчные буквы
греческого алфавита ξ - (кси),ζ- (дзетта) , η- (этта) и т.д., или
заглавные буквы латинского алфавита (как принято для обозначения множеств : А, В …).
Измеримость функции ξ = ξ(ω) необходимо для того, чтобы определить вероятность:
P(ξ) = P(ω: ξ(ω) ∈ B), B⊆R(1), {ω: ξ(ω) ∈ B}∈ A.
Любому исходу ω∈Ω ВЭ в соответствии с функцией ξ(ω) устанавливается число x, которое называется реализацией случайной величины ξ. Символически это случайное событие обозначается: ω = {ξ = x}; множество X = Xξ = {x} называют множеством реализаций СВ, Xξ ⊆ R(1).

Виды случайных величин
Введение понятия СВ позволяет совершить взаимно однозначное
функциональное преобразование вероятностного пространства событий (Ω,A,P)
в вероятностное пространство чисел (X,A,P), X⊆R(1). Символически это
записывается:
(Ω,A,P) (X,A,P), X⊆R(1).
Различают три вида случайных величин:
дискретная СВ - ξ∈ Xξ, если Xξ конечно или счетно,
непрерывная СВ - ξ∈ Xξ, если Xξ не счетно,
смешанная СВ - ξ∈ Xξ, если Xξ представимо конечным или счетным объединением не счетных множеств.
Примеры.
Случайной величиной является число очков, выпавших при бросании игральной кости, или рост студента.
В первом примере мы имеем дело с дискретной случайной величиной (она
принимает значения из дискретного числового множества ) Xξ ={1, 2, 3, 4, 5, 6};
во втором примере - с непрерывной случайной величиной (она принимает
значения из непрерывного числового множества : из промежутка числовой прямой Xξ =[100, 230] ).
ξ

Дискретные случайные величины
Определение. Дискретной случайной величиной (ДСВ) называют измеримую функцию ξ = ξ(ω), принимающую конечное или счетное количество значения. В общем случае множеством реализаций ДСВ можно считать натуральный ряд чисел
{1, 2, …n, …} = N, Xξ ⊆ N.
Рассмотрим один из вариантов взаимно однозначного преобразования вероятностного пространства с конечным числом исходов в вероятностное пространство ДСВ:
(Ω(n),A,P) (X(n),A*,P*), X(n) ⊆ N.
ξ

Взаимно-однозначное отображение вероятностных пространств
Пусть Ω(n)={ωi}, А={ω1,ω2,…,ωm|ωi∈Ω, }=
А∈ A, P(A)= , P(A) [ 0,1], P(A) ∈ P.
Если X(n) = { xi }, ωi ↔ xi , ωi = {ξ = xi }, тогда A ↔ A*,
A*={x1,x2,…,xm|xi∈ X(n), }= , А*∈A*,
P(A*)=P(A)= = =P( );
Распределение вероятностей:
↔

Задание случайной величины
Распределение вероятностей исчерпывающим образом определяет случайную величину.
Для того чтобы задать ДСВ в вероятностном пространстве (Ω,A,P), необходимо и достаточно на множестве реализации СВ задать распределение вероятностей, т.е.
ξ:
Вероятностные эксперименты в (Ω,A,P) могут моделироваться случайными величинами с определенным законом распределения вероятностей. В дальнейшем исследования ВЭ сводится к заданию соответствующей случайной величины и анализа её закона распределения.

Способы задания и представления ДСВ
Основными способами задания СВ являются:
аналитический (используются функции действительного и комплексного переменного для описания законов распределения и свойств СВ);
табличный (таблицы распределения, вероятностные ряды);
графический (применяются графики, диаграммы, схемы для наглядного представления распределений и случайных величин) .
С каждым из них познакомимся на следующем примере

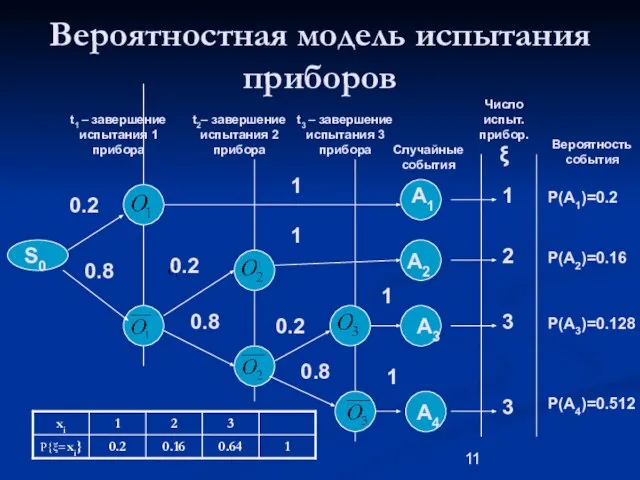
Пример задания ДСВ
Пример. С помощью ДСВ описать ВЭ: «Последовательное испытание трех приборов на надежность. Первый, затем каждый последующий прибор испытывается только в том случае, если предыдущий не отказал за конечное время в процессе испытания ». Вероятность выдержать испытания для каждого прибора равна 0,8.
Для удобства элементарные исходы и вероятности в числовом вероятностном пространстве в дальнейшем будем обозначать: Ai = ωi ={ξ = xi },
Вер{Ai}=P(Ai)=P(ωi)=Вер{ξ = xi }= P{ξ = xi }= p(xi)=pi и пользоваться данной символикой по обстоятельствам.

Принятые условные обозачения
Опишем ВЭ в виде двоичного дерева со
взвешенными дугами. Веса дуг равны вероятностям:
вероятности отказа i прибора при испытании ( Oi) : P( Oi) = 0,2 ;
вероятности не отказа прибора при испытании ( ): P( )= 0,8.
Возможные исходы испытания каждого прибора образуют ПГС. Отказы испытуемых приборов будем считать независимыми событиями :
P(O2|O1) = P(O2| )= P( Oi) = 0,2
P( |O1) = P( | )= P( )= 0,8 и т.п.

Вероятностная модель испытания приборов
t1 – завершение испытания 1 прибора
t2– завершение испытания 2 прибора
t3 – завершение испытания 3 прибора
Случайные события
Число испыт. прибор. ξ
Вероятность события
A1
A2
A3
A4
1
2
3
3
S0
0.2
0.8
0.2
0.8
0.2
0.8
1
1
1
1
P(A1)=0.2
P(A2)=0.16
P(A3)=0.128
P(A4)=0.512

Определение вероятностей
Пусть ДСВ ξ описывает число испытуемых приборов. Множество реализаций ДСВ ξ : Xξ = {1, 2, 3}
Вероятности событий:
P{ξ =1} = P(A1) = P( O1) = 0,2
P{ξ =2} = P(A2) = P(O2| ) P( ) = P( )P( O2)=0,8 *0.2=0.16
P{ξ =3} = P(A3 U A4) = P(A3)+P(A4) =0,8 *0.8*( 0.2+0.8) =0.64
P{ξ =1}+P{ξ =2}+ P{ξ =3} = 0,2+0.16+ 0.64= 1
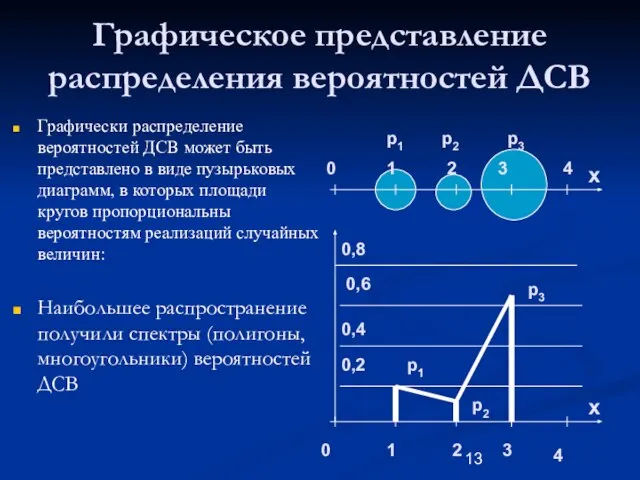
Распределение вероятностей ДСВ принято записывать в виде таблицы:

Графическое представление распределения вероятностей ДСВ
Графически распределение вероятностей ДСВ может быть представлено в виде пузырьковых диаграмм, в которых площади кругов пропорциональны вероятностям реализаций случайных величин:
Наибольшее распространение получили спектры (полигоны, многоугольники) вероятностей ДСВ
x
2
0
3
4
1
x
0
1
2
3
4
0,2
0,4
0,6
0,8
p3
p2
p1
p1
p2
p3

Функциональное задание ДСВ
Наряду с заданием распределения вероятностей ДСВ в виде вероятностного ряда : ξ : {(xi, P (xi) | xi∈ Xξ, =1 } ,
широко пользуются так же задание распределения вероятностей:
функцией вероятностей,
функцией распределения вероятностей,
характеристической функцией и т.д.
Каждая из этих функций являются "паспортом" случайной величины, так как они содержат всю информацию об этой случайной величине, и поэтому изучение случайной величины заключается в исследовании этих функций, которые часто объединяют общим называнием закон распределения. Так что, когда говорят о нормальном или о другом законе распределения, то подразумевают случайную величину, имеющую нормальную функцию распределения и т.д. В дальнейшем будем широко использовать термин закон распределения вероятностей, подразумевая задание СВ одним из возможных способов.

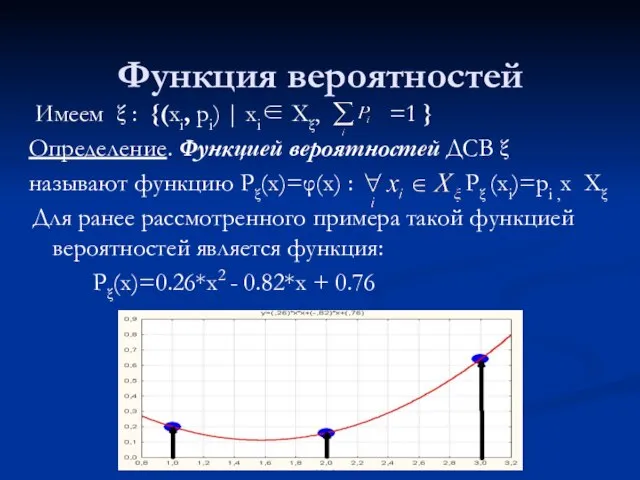
Функция вероятностей
Имеем ξ : {(xi, pi) | xi∈ Xξ, =1 }
Определение. Функцией вероятностей ДСВ ξ
называют функцию Pξ(x)=φ(x) : Pξ (xi)=pi ,x Xξ
Для ранее рассмотренного примера такой функцией вероятностей является функция:
Pξ(x)=0.26*x2 - 0.82*x + 0.76

Функцией распределения вероятностей ДСВ
Определение. Функцией распределения вероятностей ДСВ ξ называют функцию :
F (x) = Fξ(x) = P(ξ < x) = .
Здесь P(ξ
Функции распределения любой случайной величины обладает следующими свойствами:
1) Fξ(x) определена на всей числовой прямой R(1) = (-∞, +∞);
2) Fξ(- ∞) = 0 и Fξ(+∞) = 1, т. е. и

Свойства функции распределения
3) Fξ (x) - неубывающая функция,
т.е. если x1 ≤ x2, то Fξ(x1) ≤ Fξ(x2)
4) Fξ(x) - функция непрерывна слева,
т.е.
5)
5.1) P(ξ=x) = Fξ (x +0)- Fξ (x)

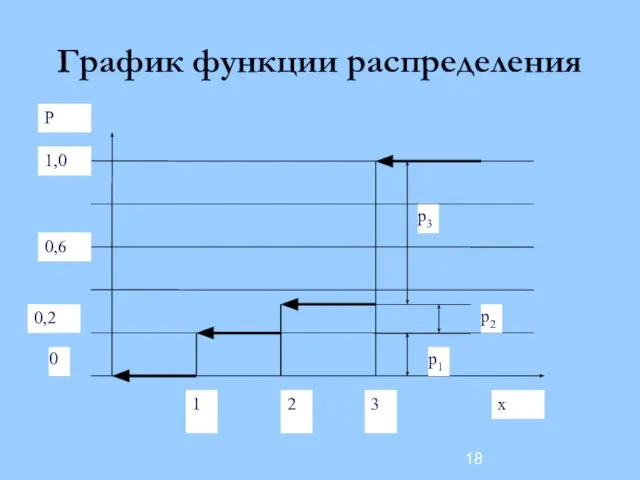
График функции распределения

Законы распределения ДСВ
Законы распределения случайных величин получивших широкое распространение как для аналитического описания вероятностных экспериментов, так и для применения в различных приложениях получили название типовых.
К числу типовых обычно относят:
Дискретные распределения (ДСВ) - вырожденное распределение, распределение Бернулли, биномиальное (полиномиальное), геометрическое (гипергеометрическое), Пуассона и др.

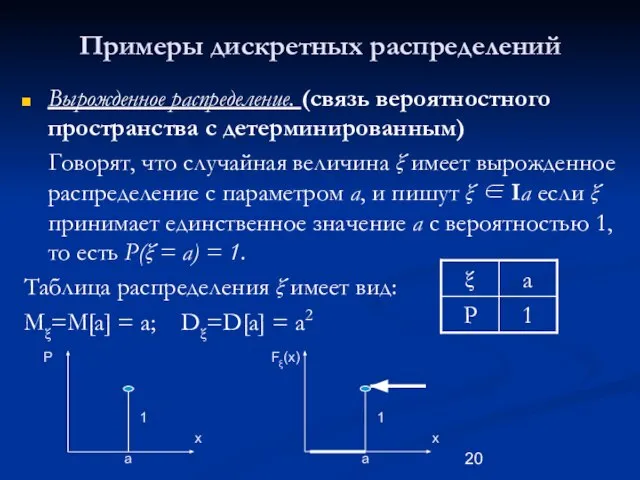
Примеры дискретных распределений
Вырожденное распределение. (связь вероятностного пространства с детерминированным)
Говорят, что случайная величина ξ имеет вырожденное распределение с параметром а, и пишут ξ ∈ Ia если ξ принимает единственное значение а с вероятностью 1, то есть P(ξ = a) = 1.
Таблица распределения ξ имеет вид:
Mξ=M[a] = a; Dξ=D[a] = a2
a

Примеры дискретных распределений
Распределение Бернулли. Случайная величина ξ имеет распределение Бернулли, если она принимает всего два значения: 1 и 0 с вероятностями p соответственно.
Таким образом: P{ξ=0}=q; P{ξ=1}=p; (p+q)=1; Xξ={0; 1}.
Принято говорить, что событие {ξ = 1} соответствует «успеху», а {ξ = 0} «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
Таблица распределения ξ имеет вид:

Характеристики распределения Бернулли

Биномиальное распределение
Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна p. (Данная схема испытаний называются системой испытаний Бернулли).
Формально оно определяется: Пусть ξ1, ξ2, …, ξn — конечная последовательность n независимых случайных величин (ξi{0;1})с распределением Бернулли.
η= ξ1+ ξ2+ …+ ξn : ДСВ η  {0, 1, …, n} называют биномиально распределенной, если функция вероятностей Pη(k)=Вер{η=k}= Bin(p,n,k) = C(k, n)рk (1-p)n-k ,
где биномиальные коэффициента
разложения функции (q+p)n в ряд по степеням p и q (бином
Ньютона)

Биномиальное распределение
η= ξ1+ ξ2+ …+ ξn можно интерпретировать как число единиц (успехов) в последовательности ξ1, ξ2, …, ξn .
Функция распределения биномиального распределения может быть записана в виде суммы:
yk{0,1, …, n}, q=1-p
Производящая функция моментов биномиального распределения имеет вид: qη(t)=M[etη]=(pet+q)n
Моменты: ,
Dη=μ2=α2-(α1)2 =npq, Aη=(1-2p)/(nhq)1/2; Eη=((1-6pq)/npq) -3

Графическое представление биномиального распределения

Приложение
Примеры решения задач