Lektsia_9_Zatukh_i_vynuzh_kol_ZS

Затухающие колебания
Уменьшение амплитуды колебания ведет к потере энергии, т.к.
Свободные колебания с уменьшающейся амплитудой называют затухающими
уравнение движения груза
на пружине в стакане воды:
Обычно, в механической колебательной системе потери энергии связаны с трением
Вязкое трение:
где r – коэффициент сопротивления
или другая форма записи
Рассмотрим на примере пружинного маятника (груз на пружине
в стакане с водой)

Дифференциальное уравнение затухающих колебаний
Дифференциальное уравнение затухающих колебаний пружинного маятника в вязкой среде
Разделим на m и преобразуем
собственная частота колебаний
β – коэффициент затухания
Учитывая, что
получим
Дифференциальное уравнение затухающих колебаний
для любой колебательной системы с сопротивлением, пропорциональным скорости
Частным случаем этого уравнения является уравнение незатухающих колебаний (при β=0)

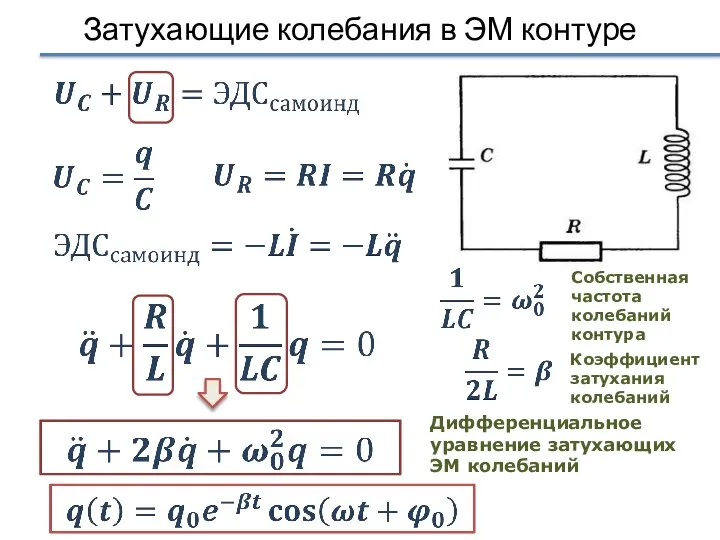
Затухающие колебания в ЭМ контуре
Дифференциальное уравнение затухающих ЭМ колебаний
Собственная частота колебаний контура
Коэффициент затухания колебаний

Решение дифференциального уравнения
затухающих колебаний
В зависимости от соотношения между собственной частотой системы
и коэффициентом затухания возможны три типа решения:
– колебательный режим
– критический режим
– апериодический режим
Дифференциальное уравнение затухающих колебаний
решение дифференциального уравнения:
При
где
частота затухающих колебаний
амплитуда затухающих колебаний
Затухающие колебания подчиняются закону
механические колебания

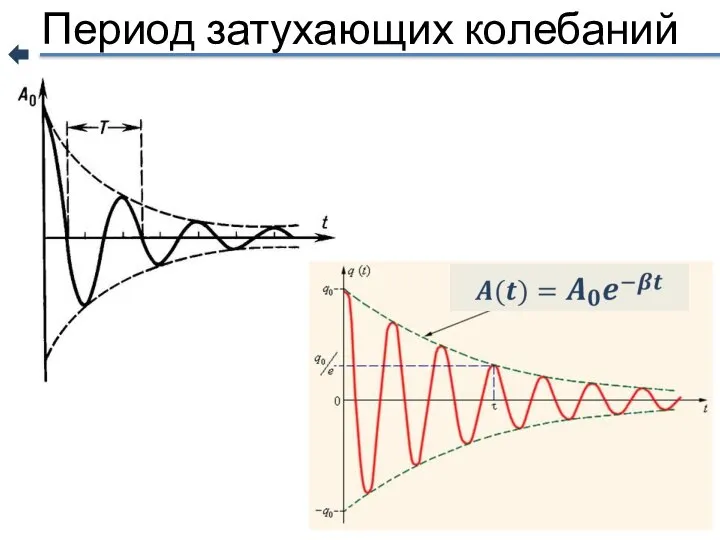
Параметры затухающих колебаний
Частота
затухающих колебаний
Амплитуда
затухающих колебаний
Начальная амплитуда
Период
затухающих колебаний
Время релаксации
Коэффициент затухания
Логарифмический декремент затухания
Добротность
колебательной
системы
механические
ЭМ
механические
ЭМ
механические
ЭМ

Период затухающих колебаний

Время релаксации
промежуток времени, за который амплитуда затухающих колебаний уменьшается в е раз
Коэффициент затухания
обратно пропорционален времени релаксации
показывает во сколько раз амплитуда уменьшается за единицу времени
Время релаксации
обратно пропорционально
коэффициенту затухания

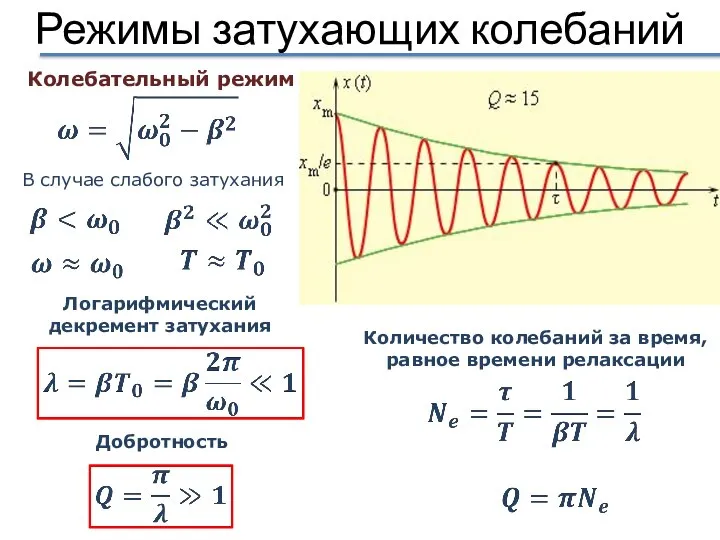
Логарифмический декремент затухания
натуральный логарифм двух последовательных амплитуд
Характеризует степень затухания –
показывает за какое количество колебаний амплитуда уменьшается в е раз
Логарифмический декремент затухания
Пусть
тогда
т.е. за одно колебание
амплитуда уменьшится
в e раз
Пусть
тогда
амплитуда уменьшится
в е раз за 3 колебания
или:
Величина, постоянная для данной колебательной системы
Ne – количество колебаний за время уменьшения амплитуды в е раз

Добротность колебательной системы
Q – характеризует потери энергии колебательной системы за период
Добротность означает качественность:
чем больше добротность системы,
тем ближе она к идеальной,
тем медленнее затухают колебания

При малых затуханиях можно считать, что энергия в колебательной системе изменяется по закону
где
Ео- значение энергии в начальный момент времени. Продифференцируем это выражение по времени:
Скорость убывания энергии со временем
Если за период энергия мало изменяется, то при умножении этого выражения на T можно найти убыль энергии за период и выразить добротность через энергию.

Режимы затухающих колебаний
В случае слабого затухания
Колебательный режим
Логарифмический
декремент затухания
Добротность
Количество колебаний за время, равное времени релаксации

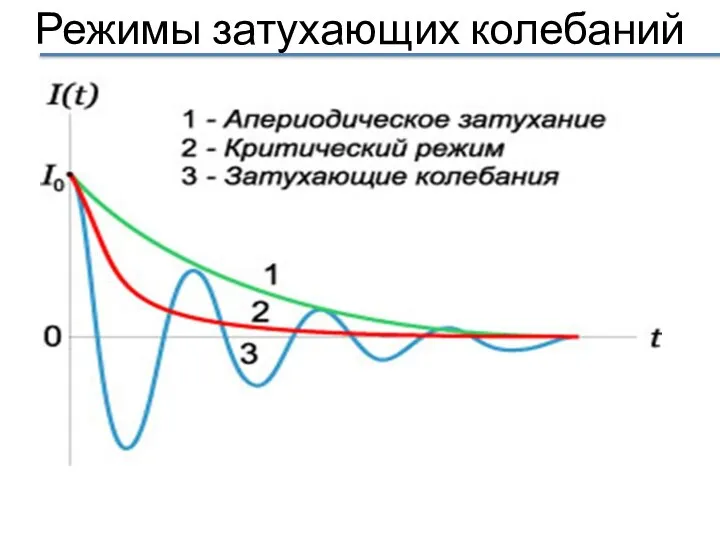
Режимы затухающих колебаний

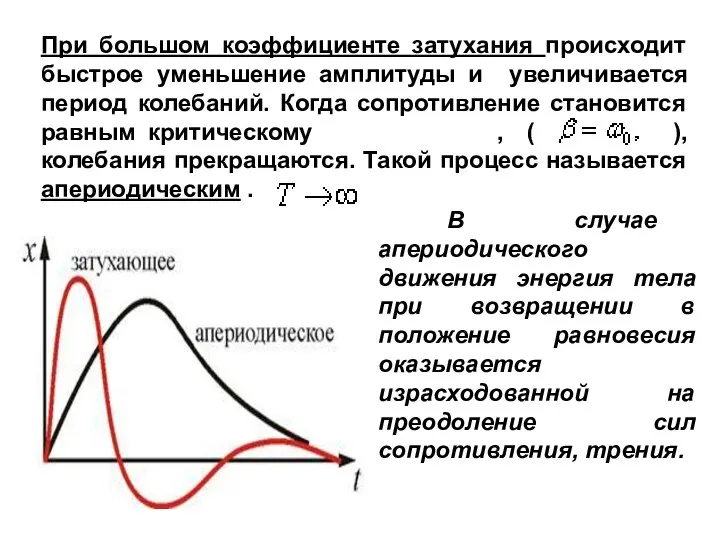
При большом коэффициенте затухания происходит быстрое уменьшение амплитуды и увеличивается период колебаний. Когда сопротивление становится равным критическому , ( ), колебания прекращаются. Такой процесс называется апериодическим .
В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения.

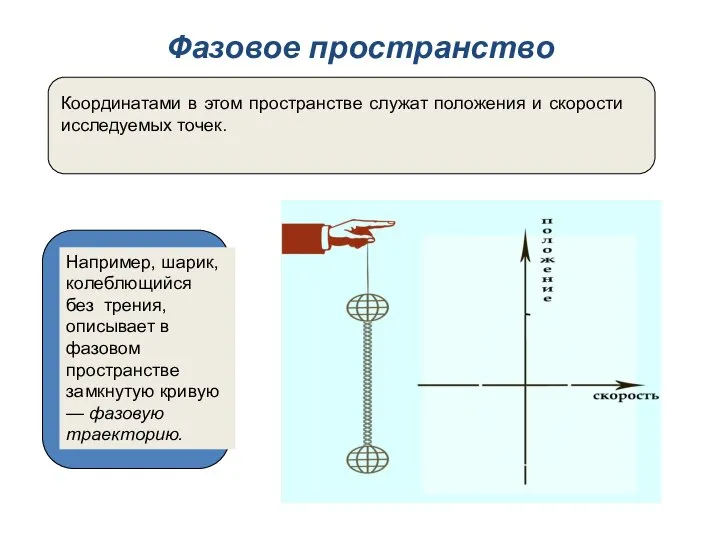
Фазовое пространство
Координатами в этом пространстве служат положения и скорости исследуемых точек.
Например, шарик, колеблющийся без трения, описывает в фазовом пространстве замкнутую кривую — фазовую траекторию.

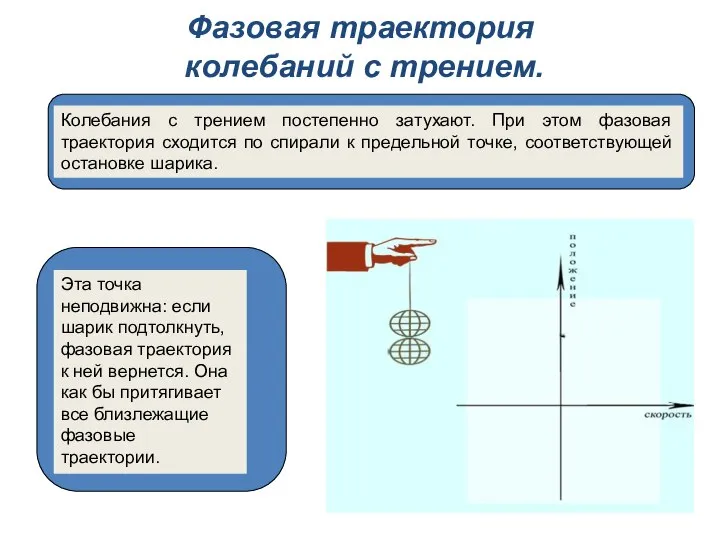
Фазовая траектория
колебаний с трением.
Колебания с трением постепенно затухают. При этом фазовая траектория сходится по спирали к предельной точке, соответствующей остановке шарика.
Эта точка неподвижна: если шарик подтолкнуть, фазовая траектория к ней вернется. Она как бы притягивает все близлежащие фазовые траектории.

Вынужденные
колебания

Вынужденные колебания
Свободные колебания
реальной колебательной системы всегда являются затухающими
Что можно/нужно сделать, чтобы ослабить/исключить затухание?
Будем воздействовать на колеблющуюся систему внешней вынуждающей силой F, изменяющейся
по гармоническом закону
Возникающие при этом в системе колебания называются вынужденными
колебания, возникающие
под действием внешней периодически изменяющейся силы
Итак,
Вынужденные колебаний
Чтобы возбудить в такой системе незатухающие колебания, необходимо компенсировать потери энергии, обусловленные трением колебаний

Уравнение вынужденных колебаний
Силы, действующие на систему
Разделим это уравнение на m, перенесем члены, содержащие x в левую часть:
Неоднородное линейное дифференциальное уравнение
второго порядка с постоянными коэффициентами:
Вынуждающая сила
Квазиупругая сила
Результирующая сила
Сила сопротивления
Собственная частота
Коэффициент затухания
Амплитуда
вынуждающей силы

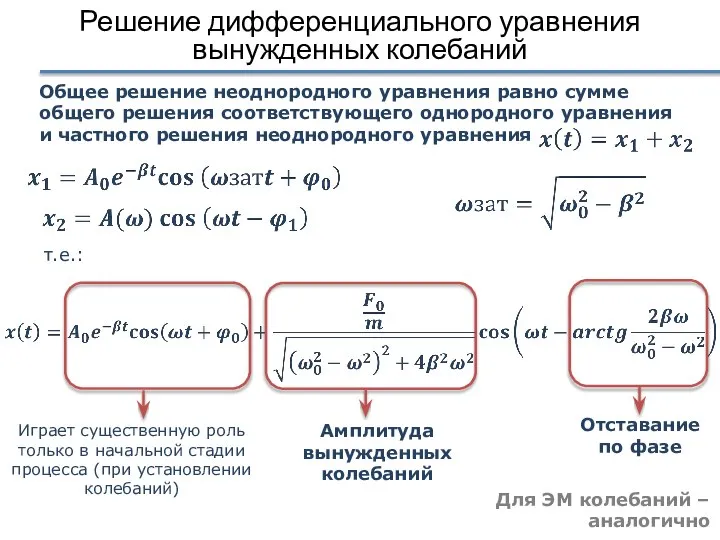
Решение дифференциального уравнения вынужденных колебаний
Общее решение неоднородного уравнения равно сумме
общего решения соответствующего однородного уравнения
и частного решения неоднородного уравнения
Амплитуда вынужденных колебаний
т.е.:
Играет существенную роль только в начальной стадии процесса (при установлении колебаний)
Отставание
по фазе
Для ЭМ колебаний – аналогично

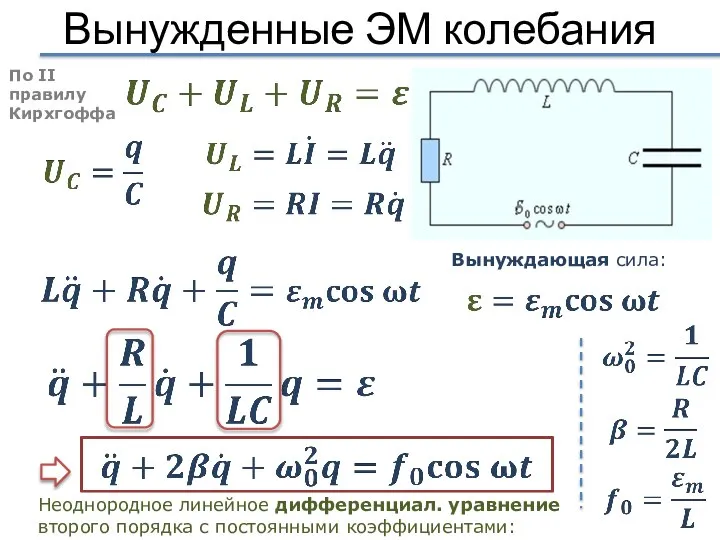
Вынужденные ЭМ колебания
По II правилу Кирхгоффа
Вынуждающая сила:
Неоднородное линейное дифференциал. уравнение
второго порядка с постоянными коэффициентами:

Уравнение вынужденных электромагнитных колебаний
Вынуждающая сила:
Решение уравнения :

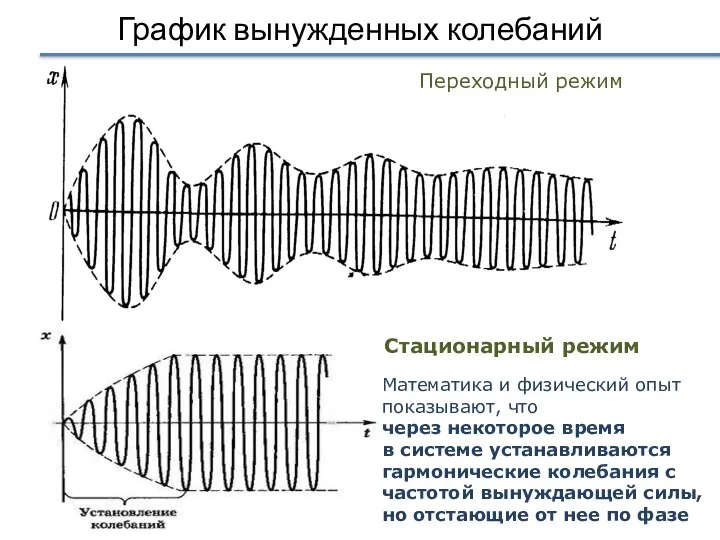
График вынужденных колебаний
Стационарный режим
Переходный режим
Математика и физический опыт показывают, что
через некоторое время
в системе устанавливаются гармонические колебания с частотой вынуждающей силы, но отстающие от нее по фазе

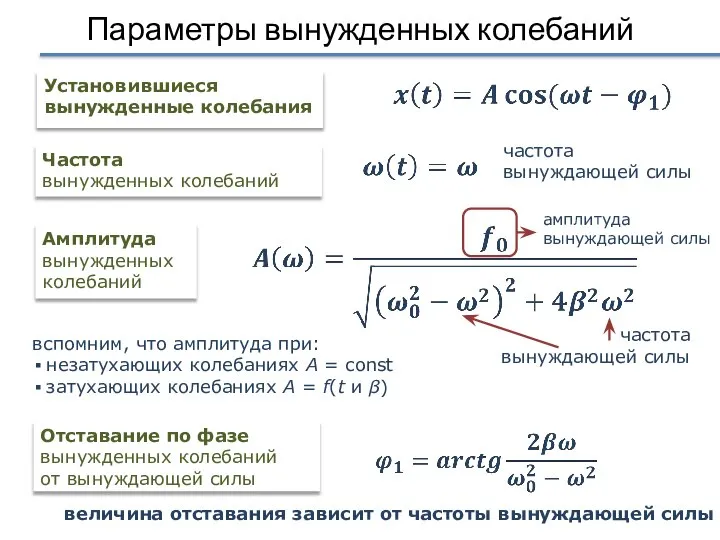
Параметры вынужденных колебаний
Отставание по фазе вынужденных колебаний
от вынуждающей силы
Установившиеся вынужденные колебания
Амплитуда
вынужденных колебаний
частота
вынуждающей силы
от чего зависит?
амплитуда вынуждающей силы
вспомним, что амплитуда при:
незатухающих колебаниях А = const
затухающих колебаниях A = f(t и β)
Частота
вынужденных колебаний
частота
вынуждающей силы
величина отставания зависит от частоты вынуждающей силы

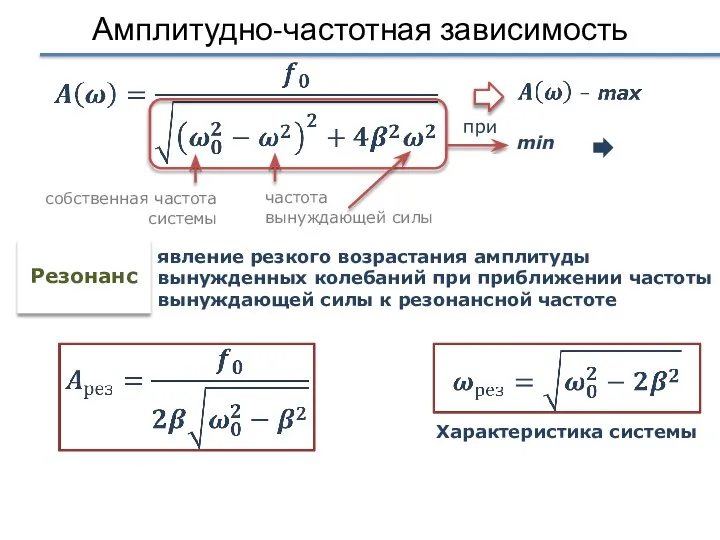
Амплитудно-частотная зависимость
min
явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к резонансной частоте
Резонанс
частота вынуждающей силы
Характеристика системы
собственная частота системы
при

Резонансная частота
при
?
Полученное уравнение имеет два решения:
«-» не имеет физического смысла, остается со знаком «+»

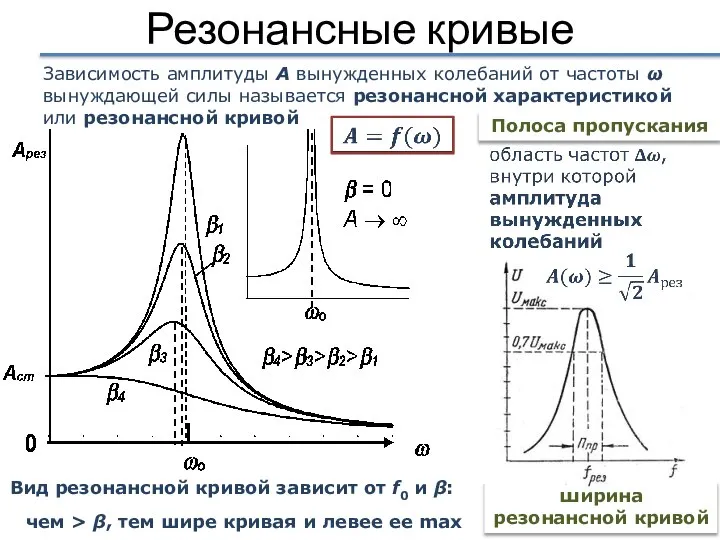
Резонансные кривые
Вид резонансной кривой зависит от f0 и β:
чем > β, тем шире кривая и левее ее max
Полоса пропускания
Ширина
резонансной кривой
Зависимость амплитуды А вынужденных колебаний от частоты ω вынуждающей силы называется резонансной характеристикой или резонансной кривой

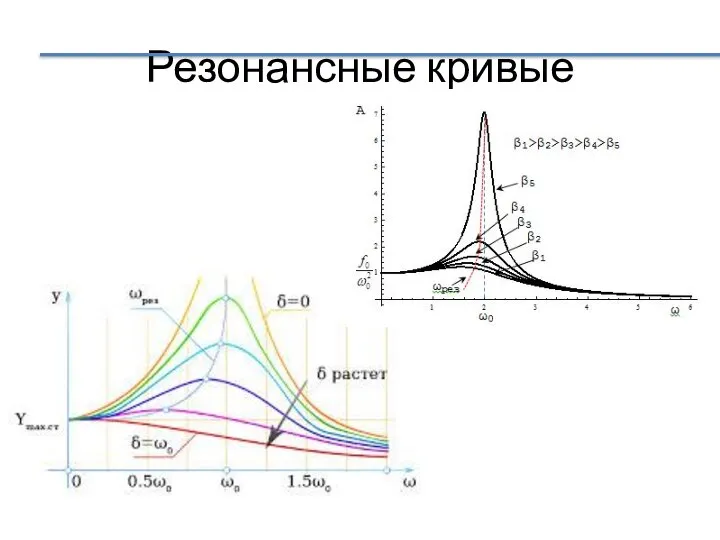
Резонансные кривые

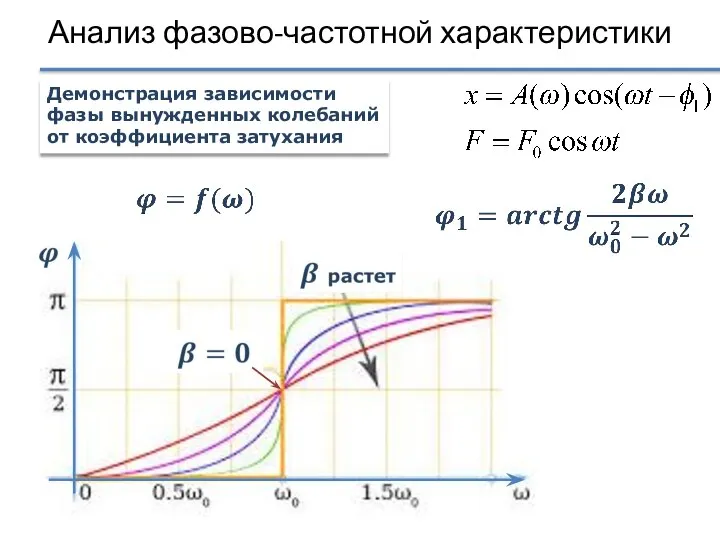
Анализ фазово-частотной характеристики
Демонстрация зависимости
фазы вынужденных колебаний
от коэффициента затухания

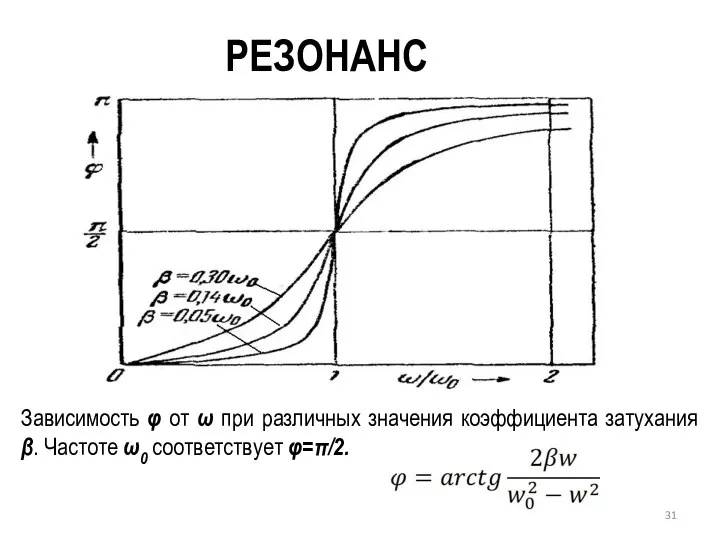
РЕЗОНАНС
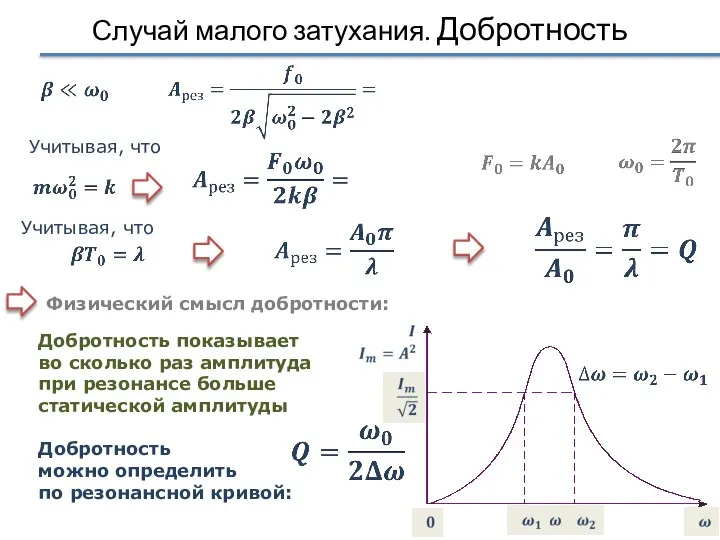
Зависимость φ от ω при различных значения коэффициента затухания β. Частоте ω0 соответствует φ=π/2.

Случай малого затухания. Добротность
Добротность показывает
во сколько раз амплитуда
при резонансе больше статической амплитуды
Учитывая, что
Учитывая, что
Физический смысл добротности:
Добротность
можно определить
по резонансной кривой:

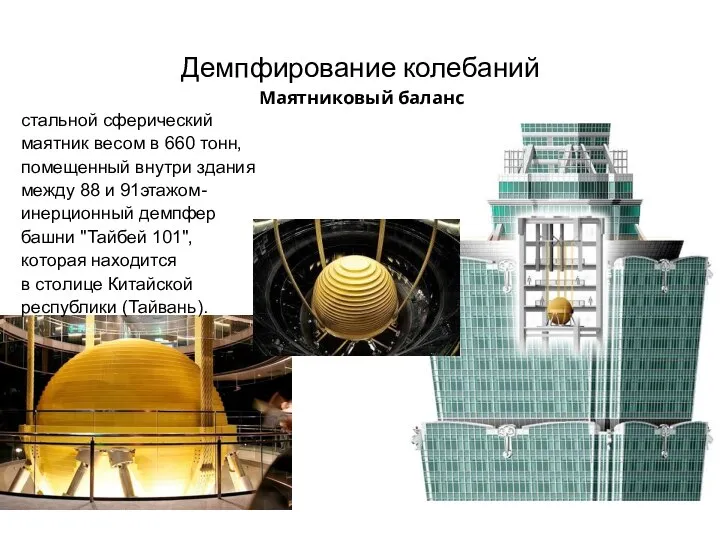
Демпфирование колебаний
стальной сферический маятник весом в 660 тонн, помещенный внутри здания между 88 и 91этажом-инерционный демпфер башни "Тайбей 101", которая находится в столице Китайской республики (Тайвань).
Маятниковый баланс

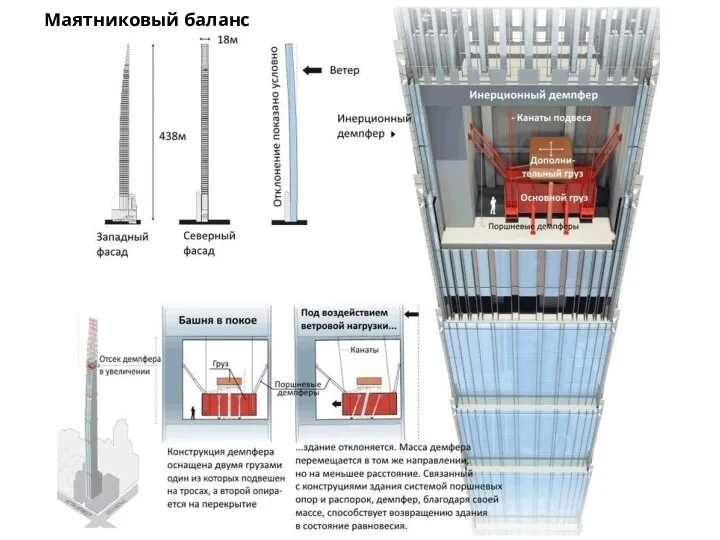
Демпфирование колебаний
Маятниковый баланс

Демпфирование колебаний
Шанхай

Сингапурский отель Marina Bay Sands
прославился на весь мир свои потрясающим бассейном на крыше, соединяющей сразу три башни отеля. Но отдыхающие и не подозревают, что плавают по сути в огромном демпфере. Вода в бассейне компенсирует колебания во время подземных толчков.
Демпфирование колебаний