Линейная функция 11 класс

Линейная функция
Определение линейной функции
Свойство линейной функции
Описание
График линейной функции
График 1 (рис. 1)
Пример 1
Пример 2
Замечание к примерам
Пример 3
Замечание к примеру 3
Пример 4
Пример 5
Частный случай
График 2 (рис. 2)
Пример 6
Содержание

Линейные Функции
Рассмотрим сначала наиболее простую функцию, а не линейную: y(x)=kx+b, где k и b- некоторые константы, x и y- переменные.
График линейной функции- прямая линия. Прямая Y=kx+l пересекает ось ординат в точке (o;l) и ось абсцисс в точке (-l/k;o).
Число k- угловой коэффициент прямой.

Определение линейной функции
Линейная функция – двучлен первой степени, т. е. функция вида y=kx+b.Линейная функция определена на всей числовой потому, что ее график есть прямая линия.
Рассмотрим два значения аргумента x1 и x2, им соответствует значения линейной функции y1=ax1+b и y2=ax2+b. Изменение аргумента на величине x2-x1 называется изменение функции на величине y2-y1=a(x2-x1) при этом отношении изменения функции к изменению аргумента равно а: (y2-y1)/(x2-x1)=a

Свойство линейной функции
Таким образом, у линейной функции изменение функции пропорционально изменению аргумента, и это есть характеристическое свойство линейной функции. Поэтому с помощью линейной функции описывается пропорциональные зависимости.

Описание
Пример пропорциональной зависимости дает зависимость между различными шкалами температур абсолютная температура tk (по Кельвину) связана с температурой tc на шкале Цельсия формулой tc=tk+273°, а переход от температуры по Фаренгейту (шкале, принятой до сих пор в Англии и США) tф к температуре на шкале Цельсия tс выражается такой линейной функцией: tф=1,8tс+32° (на шкале Цельсия промежуток между точкой замерзания и точкой кипения разделен на 100 частей, а на шкале Фаренгейта на 180, и 0°С соответствует 32°Ф)

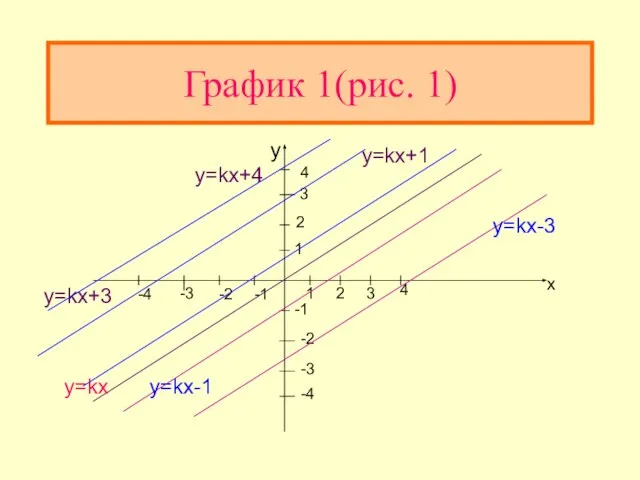
График линейной функции
График линейной функции y=kx+b (b не равно 0) получается из графика функции y=ax параллельным переносом на b единиц вверх при b>0 и на b единиц вниз при b<0 (рис. 2). Поскольку прямая определяется своими двумя точками, то для построения графика достаточно лишь двух ее точек.
Линейная функция простейшая и, можно сказать, важнейшая среди всех функций. Многие физические законы выражаются с помощью линейной функции (мы уже говорили о пройденном пути при постоянной скорости), но важно то, что целый ряд сложных нелинейных зависимостей «в малом» можно считать линейным.

График 1(рис. 1)
x
-1
-2
-3
-4
4
3
2
1
-1
-2
-3
-4
1
2
3
4
y=kx
y=kx+1
y=kx+3
y=kx+4
y=kx-1
y=kx-3
y

Дано уравнение: -2x+3y=6. Выразим переменную y через x. Имеем линейную функцию: , где k=2/3; l=2. Так как k=2/3>0, то функция возрастает на всей области определения.
Пример 1
x
-3
2
-1
1
0
y

Пример 2
2/3x4y=1
Y=1/10x+1/4; где k=-1/10; l=1/4
Так как k=-1/10<0, то функция Y=-1/10x+1/4 убывает на всей области определения.
y
x
1 2
1
1
Y=-1/10x+1/4

Замечание 1 к примеру 2
Функция прямая пропорциональность y=kx является частным случаем функции y=kx+b (при l=0).
Замечание 2 к примеру 2
Графиком линейной функции y=l(k=0) является прямая, параллельная оси абсцисс, пересекающая ось ординат в точке(o;l)

Пример 3
Y=-2
Подчеркнем, что уравнение X=k не является функцией. Поскольку нарушается условие однозначности при определении функции- каждому значению x должно соответствовать единственное значение y.
x
y
0
-1
-2
Y=-2
1

Замечание к примеру 3
Графиком уравнения x=k является прямая, параллельная оси пересекающая ось Oy, абсцисс в точке (k;o)

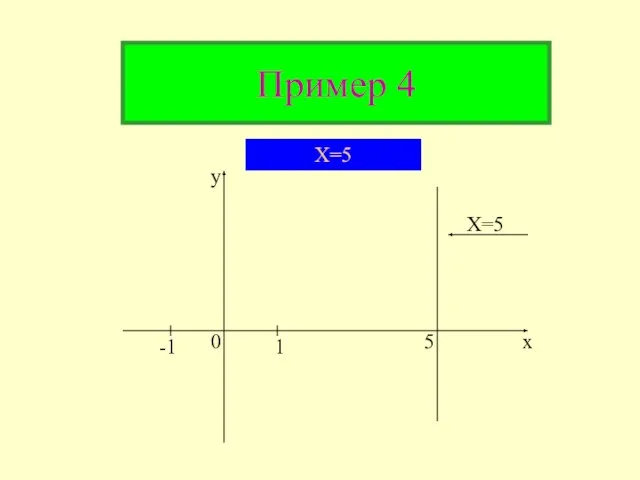
Пример 4
y
x
-1
1
0
5
X=5
X=5

Пример 5
Цена р купленного отрезка ткани пропорциональна его длине l, а именно p=kl (здесь k-цена одного метра ткани); при равномерном движении с постоянной скоростью v пройденный путь s пропорционален времени t и выражается формулой s=vt, т. е. s-линейная функция t.

Частный случай
частный случай линейной функции – прямая пропорциональная зависимость y=kx, т.е.линейная функция при b=0. график этой функции есть прямая, проходящая через начало координат (рис.1). Число а называется угловым коэффициентом прямой и равен tg угла альфа, образованного прямой с положительным направлением оси 0x.

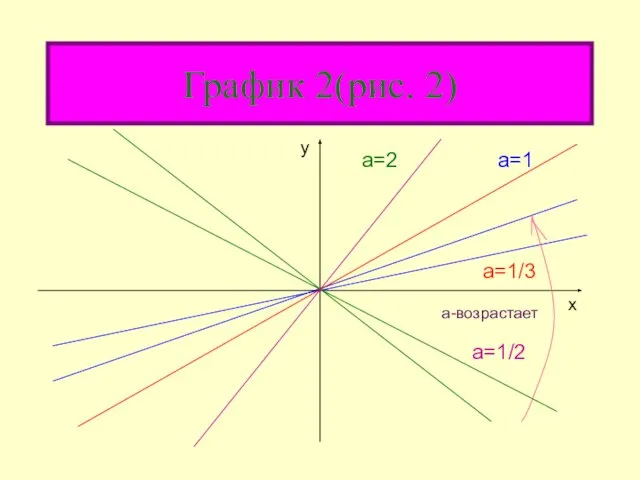
График 2(рис. 2)
График 2(рис. 2)
a=1
a=1/3
а-возрастает
y
x
a=1/2
a=2